The GAM Procedure
- Overview
- Getting Started
-
Syntax

-
Details
 Missing ValuesNonparametric RegressionAdditive Models and Generalized Additive ModelsForms of Additive ModelsEstimates from PROC GAMBackfitting and Local Scoring AlgorithmsSmoothersSelection of Smoothing ParametersConfidence Intervals for SmoothersDistribution Family and Canonical LinkDispersion ParameterComputational ResourcesODS Table NamesODS Graphics
Missing ValuesNonparametric RegressionAdditive Models and Generalized Additive ModelsForms of Additive ModelsEstimates from PROC GAMBackfitting and Local Scoring AlgorithmsSmoothersSelection of Smoothing ParametersConfidence Intervals for SmoothersDistribution Family and Canonical LinkDispersion ParameterComputational ResourcesODS Table NamesODS Graphics -
Examples

- References
This example illustrates the capabilities of the GAM procedure and compares it to the GENMOD procedure. From this example, you can see that PROC GAM is very useful in visualizing the data and detecting the nonlinearity among the variables.
The data used in this example are based on a study by Bell et al. (1994). Bell and his associates studied the result of multiple-level thoracic and lumbar laminectomy, a corrective spinal surgery
commonly performed on children. The data in the study consist of retrospective measurements on 83 patients. The specific outcome
of interest is the presence (1) or absence (0) of kyphosis, defined as a forward flexion of the spine of at least 40 degrees
from vertical. The available predictor variables are age in months at time of the operation (Age), the starting of vertebrae levels involved in the operation (StartVert), and the number of levels involved (NumVert). The goal of this analysis is to identify risk factors for kyphosis. PROC GENMOD can be used to investigate the relationship
among kyphosis and the predictors. The following statements create the data kyphosis and fit a logistic model specifying linear effects for the three predictors:
title 'Comparing PROC GAM with PROC GENMOD'; data kyphosis; input Age StartVert NumVert Kyphosis @@; datalines; 71 5 3 0 158 14 3 0 128 5 4 1 2 1 5 0 1 15 4 0 1 16 2 0 61 17 2 0 37 16 3 0 113 16 2 0 59 12 6 1 82 14 5 1 148 16 3 0 18 2 5 0 1 12 4 0 243 8 8 0 168 18 3 0 1 16 3 0 78 15 6 0 175 13 5 0 80 16 5 0 27 9 4 0 22 16 2 0 105 5 6 1 96 12 3 1 131 3 2 0 15 2 7 1 9 13 5 0 12 2 14 1 8 6 3 0 100 14 3 0 4 16 3 0 151 16 2 0 31 16 3 0 125 11 2 0 130 13 5 0 112 16 3 0 140 11 5 0 93 16 3 0 1 9 3 0 52 6 5 1 20 9 6 0 91 12 5 1 73 1 5 1 35 13 3 0 143 3 9 0 61 1 4 0 97 16 3 0 139 10 3 1 136 15 4 0 131 13 5 0 121 3 3 1 177 14 2 0 68 10 5 0 9 17 2 0 139 6 10 1 2 17 2 0 140 15 4 0 72 15 5 0 2 13 3 0 120 8 5 1 51 9 7 0 102 13 3 0 130 1 4 1 114 8 7 1 81 1 4 0 118 16 3 0 118 16 4 0 17 10 4 0 195 17 2 0 159 13 4 0 18 11 4 0 15 16 5 0 158 15 4 0 127 12 4 0 87 16 4 0 206 10 4 0 11 15 3 0 178 15 4 0 157 13 3 1 26 13 7 0 120 13 2 0 42 6 7 1 36 13 4 0 ;
proc genmod data=kyphosis descending; model Kyphosis = Age StartVert NumVert/link=logit dist=binomial; run;
The GENMOD analysis of the independent variable effects is shown in Output 41.1.1. Based on these results, the only significant factor is StartVert with a log odds ratio of –0.1972. The variable NumVert has a p-value of 0.0904 with a log odds ratio of 0.3031.
Output 41.1.1: GENMOD Analysis: Partial Output
| Comparing PROC GAM with PROC GENMOD |
| Analysis Of Maximum Likelihood Parameter Estimates | |||||||
|---|---|---|---|---|---|---|---|
| Parameter | DF | Estimate | Standard Error |
Wald 95% Confidence Limits | Wald Chi-Square | Pr > ChiSq | |
| Intercept | 1 | -1.2497 | 1.2424 | -3.6848 | 1.1853 | 1.01 | 0.3145 |
| Age | 1 | 0.0061 | 0.0055 | -0.0048 | 0.0170 | 1.21 | 0.2713 |
| StartVert | 1 | -0.1972 | 0.0657 | -0.3260 | -0.0684 | 9.01 | 0.0027 |
| NumVert | 1 | 0.3031 | 0.1790 | -0.0477 | 0.6540 | 2.87 | 0.0904 |
| Scale | 0 | 1.0000 | 0.0000 | 1.0000 | 1.0000 | ||
| Note: | The scale parameter was held fixed. |
The GENMOD procedure assumes a strict linear relationship between the predictors and the response function, which is the logit (log odds) in this model. The following SAS statements use PROC GAM to investigate a less restrictive model, with moderately flexible spline terms for each of the predictors:
title 'Comparing PROC GAM with PROC GENMOD';
proc gam data=kyphosis;
model Kyphosis (event='1') = spline(Age ,df=3)
spline(StartVert,df=3)
spline(NumVert ,df=3) / dist=binomial;
run;
The MODEL statement requests an additive model with a univariate smoothing spline for each term. The response variable option
EVENT=
chooses Kyphosis=1 (presence) as the event so that the probability of presence of kyphosis is modeled. The option DIST=BINOMIAL with binary
responses specifies a logistic model. Each term is fit by using a univariate smoothing spline with three degrees of freedom.
Of these three degrees of freedom, one is taken up by the linear portion of the fit and two are left for the nonlinear spline
portion. Although this might seem to be an unduly modest amount of flexibility, it is better to be conservative with a data
set this small.
Output 41.1.2 and Output 41.1.3 list the output from PROC GAM.
Output 41.1.2: Summary Statistics
| Note: | PROC GAM is modeling the probability that Kyphosis=1. One way to change this to model the probability that Kyphosis=0 is to specify the response variable option EVENT='0'. |
| Iteration Summary and Fit Statistics | |
|---|---|
| Number of local scoring iterations | 9 |
| Local scoring convergence criterion | 2.6635661E-9 |
| Final Number of Backfitting Iterations | 1 |
| Final Backfitting Criterion | 5.2326593E-9 |
| The Deviance of the Final Estimate | 46.610922438 |
The critical part of the GAM results is the "Analysis of Deviance" table, shown in Output 41.1.3. For each smoothing effect in the model, this table gives a ![]() test comparing the deviance between the full model and the model without the nonparametric component of this variable. The
analysis of deviance results indicate that the nonparametric effect of
test comparing the deviance between the full model and the model without the nonparametric component of this variable. The
analysis of deviance results indicate that the nonparametric effect of Age is highly significant, the nonparametric effect of StartVert is nearly significant, and the nonparametric effect of NumVert is insignificant at the 5% level.
PROC GAM can also perform approximate analysis of deviance for smoothing effects by using the ANODEV=NOREFIT option, as in the following statements:
title 'PROC GAM with Approximate Analysis of Deviance';
proc gam data=kyphosis;
model Kyphosis (event='1') = spline(Age ,df=3)
spline(StartVert,df=3)
spline(NumVert ,df=3) /
dist=binomial anodev=norefit;
run;
Output 41.1.4: Approximate Analysis of Deviance Table
| PROC GAM with Approximate Analysis of Deviance |
| Smoothing Model Analysis Approximate Analysis of Deviance |
|||
|---|---|---|---|
| Source | DF | Chi-Square | Pr > ChiSq |
| Spline(Age) | 2.00000 | 7.0888 | 0.0289 |
| Spline(StartVert) | 2.00000 | 5.0431 | 0.0803 |
| Spline(NumVert) | 2.00000 | 2.2471 | 0.3251 |
The "Approximate Analysis of Deviance" table shown in Output 41.1.4 yields similar conclusions to those of the "Analysis of Deviance" table (Output 41.1.3). In addition to fitting the model using all the specified smoothing effects, the default ANODEV=REFIT option requires fitting p additional subset models to p smoothing effects. Each submodel is fit by omitting one smoothing term from the model. By contrast, the ANODEV=NOREFIT option keeps the nonparametric terms fixed and requires a weighted least squares fit for only the parametric part of the model. Hence, GAM with the ANODEV=NOREFIT option is computationally inexpensive and is useful for obtaining approximate analysis of deviance results for models with many smoothing effects. This option assumes that the remaining nonparametric terms do not change much with the deletion of one nonparametric component. It should be used with caution when a model contains highly correlated predictors.
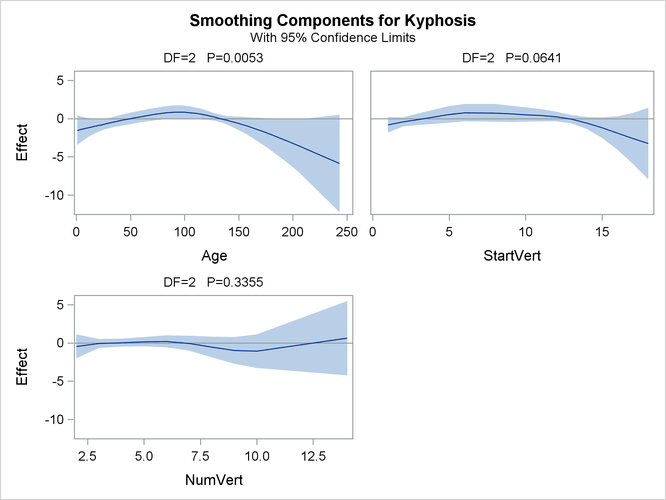
Plots of the partial predictions for each predictor can be used to investigate why PROC GAM and PROC GENMOD produce different results. The following statements use ODS Graphics to produce plots of the individual smoothing components. The CLM suboption in the PLOTS=COMPONENTS option adds a curvewise Bayesian confidence band to each smoothing component, while the COMMONAXES suboption forces all three smoothing component plots to share the same vertical axis limits, allowing a visual judgment of the relative nonparametric effect sizes.
ods graphics on;
proc gam data=kyphosis plots=components(clm commonaxes);
model Kyphosis (event='1') = spline(Age ,df=3)
spline(StartVert,df=3)
spline(NumVert ,df=3) / dist=binomial;
run;
ods graphics off;
For general information about ODS Graphics, see Chapter 21: Statistical Graphics Using ODS. For specific information about the graphics available in the GAM procedure, see the section ODS Graphics. The smoothing component plots are displayed in Output 41.1.5.
The plots show that the partial predictions corresponding to both Age and StartVert have a quadratic pattern, while NumVert has a more complicated but ultimately nonsignificant pattern.
An important difference between the first analysis of these data with PROC GENMOD and the subsequent analysis with PROC GAM
is that PROC GAM indicates that Age has a significant but nonlinear association with kyphosis. The difference is due to the fact that the generalized linear model includes only the linear effect of Age whereas the generalized additive model allows a more complex relationship, which the plots indicate is nearly quadratic.
Having used the GAM procedure to discover an appropriate form of the dependence of Kyphosis on each of the three independent variables, you can use the GENMOD procedure to fit and assess the corresponding parametric
model. The following statements fit a generalized linear model with quadratic terms for all three variables. The parameter
estimates are shown in Output 41.1.6.
title 'Comparing PROC GAM with PROC GENMOD';
proc genmod data=kyphosis descending;
model kyphosis = Age Age *Age
StartVert StartVert*StartVert
NumVert NumVert *NumVert /
link=logit dist=binomial;
run;
Output 41.1.6: Logistic Model with Quadratic Terms
| Comparing PROC GAM with PROC GENMOD |
| Analysis Of Maximum Likelihood Parameter Estimates | |||||||
|---|---|---|---|---|---|---|---|
| Parameter | DF | Estimate | Standard Error |
Wald 95% Confidence Limits | Wald Chi-Square | Pr > ChiSq | |
| Intercept | 1 | -5.8134 | 2.5618 | -10.8345 | -0.7923 | 5.15 | 0.0233 |
| Age | 1 | 0.0819 | 0.0345 | 0.0143 | 0.1496 | 5.63 | 0.0176 |
| Age*Age | 1 | -0.0004 | 0.0002 | -0.0008 | -0.0000 | 4.32 | 0.0376 |
| StartVert | 1 | 0.4394 | 0.3234 | -0.1944 | 1.0733 | 1.85 | 0.1742 |
| StartVert*StartVert | 1 | -0.0396 | 0.0202 | -0.0791 | -0.0001 | 3.86 | 0.0495 |
| NumVert | 1 | 0.3798 | 0.5988 | -0.7939 | 1.5535 | 0.40 | 0.5259 |
| NumVert*NumVert | 1 | 0.0020 | 0.0420 | -0.0803 | 0.0843 | 0.00 | 0.9621 |
| Scale | 0 | 1.0000 | 0.0000 | 1.0000 | 1.0000 | ||
| Note: | The scale parameter was held fixed. |
The p-value for the ![]() test is 0.0376 for dropping the quadratic term of
test is 0.0376 for dropping the quadratic term of Age, 0.0495 for dropping the quadratic term of StartVert, and 0.9621 for dropping this quadratic term of NumVert. The results for the quadratic GENMOD model are consistent with the GAM results.