-
ALL
-
displays all optional output except plots. When the input data set is TYPE=CORR, TYPE=UCORR, TYPE=COV, TYPE=UCOV, or TYPE=FACTOR,
simple statistics, correlations, and MSA
are not displayed.
-
ALPHA=p
-
specifies the level of confidence 1 – p for interval construction. By default, p = 0.05, corresponding to 1 – p = 95% confidence intervals. If p is greater than one, it is interpreted as a percentage and divided by 100. With multiple confidence intervals to be constructed,
the ALPHA= value is applied to each interval construction one at a time. This will not control the coverage probability of
the intervals simultaneously. To control familywise coverage probability, you might consider supplying a nonconventional p by using methods such as Bonferroni adjustment.
-
CONVERGE=p
CONV=p
-
specifies the convergence criterion for the METHOD=
PRINIT, METHOD=
ULS, METHOD=
ALPHA, or METHOD=
ML option. Iteration stops when the maximum change in the communalities is less than the value of the CONVERGE= option. The
default value is 0.001. Negative values are not allowed.
-
CORR
C
-
displays the correlation matrix or partial correlation matrix.
-
COVARIANCE
COV
-
requests factoring of the covariance matrix instead of the correlation matrix. The COV option is effective only with the METHOD=
PRINCIPAL, METHOD=
PRINIT, METHOD=
ULS, or METHOD=
IMAGE option. For other methods, PROC FACTOR produces the same results with or without the COV option.
-
COVER <=p>
CI <=p>
-
computes the confidence intervals and optionally specifies the value of factor loading for coverage detection. By default,
p = 0. The specified value is represented by an asterisk (*) in the coverage display. This is useful for determining the salience
of loadings. For example, if COVER=0.4, a display ‘0*[ ]’ indicates that the entire confidence interval is above 0.4, implying
strong evidence for the salience of the loading. See the section Confidence Intervals and the Salience of Factor Loadings for more details.
-
DATA=SAS-data-set
-
specifies the input data set, which can be an ordinary SAS data set or a specially structured SAS data set as described in
the section Input Data Set. If the DATA= option is omitted, the most recently created SAS data set is used.
-
EIGENVECTORS
EV
-
displays the eigenvectors of the reduced correlation matrix, of which the diagonal elements are replaced with the communality
estimates. When METHOD=
ML, the eigenvectors are for the weighted reduced correlation matrix. PROC FACTOR chooses the solution that makes the sum
of the elements of each eigenvector nonnegative. If the sum of the elements is equal to zero, then the sign depends on how
the number is rounded off.
-
FLAG=p
-
flags absolute values larger than p with an asterisk in the correlation and loading matrices. Negative values are not allowed for p. Values printed in the matrices are multiplied by 100 and rounded to the nearest integer (see the ROUND
option). The FLAG= option has no effect when standard errors or confidence intervals are also printed.
-
FUZZ=p
-
prints correlations and factor loadings with absolute values less than p printed as missing. For partial correlations, the FUZZ= value is divided by 2. For residual correlations, the FUZZ= value
is divided by 4. The exact values in any matrix can be obtained from the OUTSTAT=
and ODS output data sets. Negative values are not allowed. The FUZZ= option has no effect when standard errors or confidence
intervals are also printed.
-
GAMMA=p
-
specifies the orthomax weight used with the option ROTATE=
ORTHOMAX or PREROTATE=
ORTHOMAX. Alternatively, you can use ROTATE=
ORTHOMAX(p) with p representing the orthomax weight. There is no restriction on valid values for the orthomax weight, although the most common
values are between zero and the number of variables. The default GAMMA= value is one, resulting in the varimax rotation. See
the section Simplicity Functions for Rotations for more details.
-
HEYWOOD
HEY
-
sets to 1 any communality greater than 1, allowing iterations to proceed. See the section Heywood Cases and Other Anomalies about Communality Estimates for a discussion of Heywood cases.
-
HKPOWER=p
HKP=p
-
specifies the power of the square roots of the eigenvalues used to rescale the eigenvectors for Harris-Kaiser (ROTATE=
HK) rotation, assuming that the factors are extracted by the principal factor method. If the principal factor method is not
used for factor extraction, the eigenvectors are replaced by the normalized columns of the unrotated factor matrix, and the
eigenvalues are replaced by the column normalizing constants. HKPOWER= values between 0.0 and 1.0 are reasonable. The default
value is 0.0, yielding the independent cluster solution, in which each variable tends to have a large loading on only one
factor. An HKPOWER= value of 1.0 is equivalent to an orthogonal rotation, with the varimax rotation as the default. You can
also specify the HKPOWER= option with ROTATE=
QUARTIMAX, ROTATE=
BIQUARTIMAX, ROTATE=
EQUAMAX, or ROTATE=
ORTHOMAX, and so on. The only restriction is that the Harris-Kaiser rotation must be associated with an orthogonal rotation.
-
MAXITER=n
-
specifies the maximum number of iterations for factor extraction. You can use the MAXITER= option with the PRINIT, ULS, ALPHA,
or ML method. The default is 30.
-
METHOD=name
M=name
-
specifies the method for extracting factors. The default is METHOD=PRINCIPAL unless the DATA=
data set is TYPE=FACTOR, in which case the default is METHOD=PATTERN. Valid values for name are as follows:
- ALPHA | A
-
produces alpha factor analysis.
- HARRIS | H
-
yields Harris component analysis of 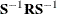 (Harris, 1962), a noniterative approximation to canonical component analysis.
(Harris, 1962), a noniterative approximation to canonical component analysis.
- IMAGE | I
-
yields principal component analysis of the image covariance matrix, not the image analysis of Kaiser (1963, 1970) or Kaiser and Rice (1974). A nonsingular correlation matrix is required.
- ML | M
-
performs maximum likelihood factor analysis with an algorithm due, except for minor details, to Fuller (1987). The option METHOD=ML requires a nonsingular correlation matrix.
- PATTERN
-
reads a factor pattern from a TYPE=FACTOR, TYPE=CORR, TYPE=UCORR, TYPE=COV, or TYPE=UCOV data set. If you create a TYPE=FACTOR
data set in a DATA step, only observations containing the factor pattern (_TYPE_=’PATTERN’) and, if the factors are correlated, the interfactor correlations (_TYPE_=’FCORR’) are required.
- PRINCIPAL | PRIN | P
-
yields principal component analysis if no PRIORS option or statement is used or if you specify PRIORS=
ONE; if you specify a PRIORS statement or a PRIORS=
value other than PRIORS=
ONE, a principal factor analysis is performed.
- PRINIT
-
yields iterated principal factor analysis.
- SCORE
-
reads scoring coefficients (_TYPE_=’SCORE’) from a TYPE=FACTOR, TYPE=CORR, TYPE=UCORR, TYPE=COV, or TYPE=UCOV data set. The data set must also contain either
a correlation or a covariance matrix. Scoring coefficients are also displayed if you specify the OUT=
option.
- ULS | U
-
produces unweighted least squares factor analysis.
-
MINEIGEN=p
MIN=p
-
specifies the smallest eigenvalue for which a factor is retained. If you specify two or more of the MINEIGEN=
, NFACTORS=
, and PROPORTION=
options, the number of factors retained is the minimum number satisfying any of the criteria. The MINEIGEN=
option cannot be used with either the METHOD=
PATTERN or the METHOD=
SCORE option. Negative values are not allowed. The default is 0 unless you omit both the NFACTORS=
and the PROPORTION=
options and one of the following conditions holds:
-
If you specify the METHOD=
ALPHA or METHOD=
HARRIS option, then MINEIGEN=
1.
-
If you specify the METHOD=
IMAGE option, then
-
For any other METHOD=
specification, if prior communality estimates of 1.0 are used, then
When an unweighted correlation matrix is factored, this value is 1.
-
MSA
-
produces the partial correlations between each pair of variables controlling for all other variables (the negative anti-image
correlations) and Kaiser’s measure of sampling adequacy (Kaiser, 1970; Kaiser and Rice, 1974; Cerny and Kaiser, 1977).
-
NFACTORS=n
NFACT=n
N=n
-
specifies the maximum number of factors to be extracted and determines the amount of memory to be allocated for factor matrices.
The default is the number of variables. Specifying a number that is small relative to the number of variables can substantially
decrease the amount of memory required to run PROC FACTOR, especially with oblique rotations. If you specify two or more of
the NFACTORS=, MINEIGEN=
, and PROPORTION=
options, the number of factors retained is the minimum number satisfying any of the criteria. If you specify the option NFACTORS=0,
eigenvalues are computed, but no factors are extracted. If you specify the option NFACTORS=–1, neither eigenvalues nor factors
are computed. You can use the NFACTORS=
option with the METHOD=
PATTERN or METHOD=
SCORE option to specify a smaller number of factors than are present in the data set.
-
NOBS=n
-
specifies the number of observations. If the DATA=
input data set is a raw data set, nobs is defined by default to be the number of observations in the raw data set. The NOBS= option overrides this default definition.
If the DATA=
input data set contains a covariance, correlation, or scalar product matrix, the number of observations can be specified
either by using the NOBS= option in the PROC FACTOR statement or by including a _TYPE_=’N’ observation in the DATA=
input data set.
-
NOCORR
-
prevents the correlation matrix from being transferred to the OUTSTAT=
data set when you specify the METHOD=
PATTERN option. The NOCORR option greatly reduces memory requirements when there are many variables but few factors. The NOCORR
option is not effective if the correlation matrix is required for other requested output; for example, if the scores or the
residual correlations are displayed (for example, by using the SCORE, RESIDUALS
, or ALL
option).
-
NOINT
-
omits the intercept from the analysis; covariances or correlations are not corrected for the mean.
-
NOPRINT
-
suppresses the display of all output. Note that this option temporarily disables the Output Delivery System (ODS). For more
information, see Chapter 20: Using the Output Delivery System.
-
NOPROMAXNORM | NOPMAXNORM
-
turns off the default row normalization of the prerotated factor pattern, which is used in computing the promax target matrix.
-
NORM=COV | KAISER | NONE | RAW | WEIGHT
-
specifies the method for normalizing the rows of the factor pattern for rotation. If you specify the option NORM=KAISER, Kaiser’s
normalization is used 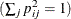 . If you specify the option NORM=WEIGHT, the rows are weighted by the Cureton-Mulaik technique (Cureton and Mulaik, 1975). If you specify the option NORM=COV, the rows of the pattern matrix are rescaled to represent covariances instead of correlations.
If you specify the option NORM=NONE or NORM=RAW, normalization is not performed. The default is NORM=KAISER.
. If you specify the option NORM=WEIGHT, the rows are weighted by the Cureton-Mulaik technique (Cureton and Mulaik, 1975). If you specify the option NORM=COV, the rows of the pattern matrix are rescaled to represent covariances instead of correlations.
If you specify the option NORM=NONE or NORM=RAW, normalization is not performed. The default is NORM=KAISER.
-
NPLOTS | NPLOT=n
-
specifies the number of factors to be plotted. The default is to plot all factors. The smallest allowable value is 2. If you
specify the option NPLOTS=n, all pairs of the first n factors are plotted, producing a total of 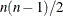 plots.
plots.
-
OUT=SAS-data-set
-
creates a data set containing all the data from the DATA=
data set plus variables called Factor1, Factor2, and so on, containing estimated factor scores. The DATA=
data set must contain multivariate data, not correlations or covariances. You must also specify the NFACTORS=
option to determine the number of factor score variables. If you specify partial variables in the PARTIAL statement, the
OUT= data set will also contain the residual variables that are used for factor analysis. The output data set is described
in detail in the section Output Data Sets. If you want to create a SAS data set in a permanent library, you must specify a two-level name. For more information about
permanent libraries and SAS data sets, see
SAS Language Reference: Concepts.
-
OUTSTAT=SAS-data-set
-
specifies an output data set containing most of the results of the analysis. The output data set is described in detail in
the section Output Data Sets. If you want to create a SAS data set in a permanent library, you must specify a two-level name. For more information about
permanent libraries and SAS data sets, see
SAS Language Reference: Concepts.
-
PARPREFIX=name
-
specifies the prefix for the residual variables in the OUT=
and the OUTSTAT=
data sets when partial variables are specified in the PARTIAL statement.
-
PLOT
-
plots the factor pattern after rotation. This option produces printer plots. High-quality ODS graphical plots for factor patterns
can be requested with the PLOTS=
LOADINGS or PLOTS=
INITLOADINGS option.
-
PLOTREF
-
plots the reference structure instead of the default factor pattern after oblique rotation.
-
PLOTS <(global-plot-options)> = plot-request <(options)>
PLOTS <(global-plot-options)> = (plot-request <(options)> <…plot-request <(options)> > )
-
specifies one or more ODS graphical plots in PROC FACTOR. When you specify only one plot-request, you can omit the parentheses around the plot-request. Here are some examples:
plots=all
plots(flip)=loadings
plots=(loadings(flip) scree(unpack))
ODS Graphics must be enabled before plots can be requested. For example:
ods graphics on;
proc factor plots=all;
run;
ods graphics off;
For more information about enabling and disabling ODS Graphics, see the section Enabling and Disabling ODS Graphics in Chapter 21: Statistical Graphics Using ODS.
For an example containing graphical displays of factor analysis results, see Example 37.2.
The following table shows the available plot-requests and their available suboptions:
|
Plot-Request
|
Plot Description
|
Suboptions
|
|
ALL
|
all available plots
|
all
|
|
INITLOADINGS
|
unrotated factor loadings
|
CIRCLE=, FLIP, NPLOTS=, PLOTREF, and VECTOR
|
|
LOADINGS
|
rotated factor loadings
|
CIRCLE=, FLIP, NPLOTS=, PLOTREF, and VECTOR
|
|
NONE
|
no ODS graphical plots
|
|
|
PATHDIAGRAM
|
path diagram
|
|
|
PRELOADINGS
|
prerotated factor loadings
|
CIRCLE=, FLIP, NPLOTS=, PLOTREF, and VECTOR
|
|
SCREE
|
scree and variance explained
|
UNPACK
|
The following are the available global-plot-options or options for plots:
- CIRCLE | CIRCLES < = numbers >
-
draws circular reference lines in scatter plots or vector plots of factor loadings. You can specify the locations of the circular
reference lines in the numbers list. Each number indicates the proportion or percentage of area of the unit circle that is enclosed by the specified circle.
Each of the numbers must lie between 0 and 100, inclusively. When a number is between 0 and 1 (inclusively), it is interpreted as a proportion;
otherwise, it is interpreted as a percentage. The maximum number of circles is 5.
The CIRCLE option applies to the scatter or vector plots requested by the INITLOADINGS, LOADINGS, and PRELOADINGS options.
By default, a unit-circle, which represents 100% of the total area, is drawn for the vector plots. However, no circle will
be drawn for scatter plots unless the CIRCLE option is specified. Two special cases for this option are: (1) With no numbers following the CIRCLE option, a 100% circle will be drawn. (2) With CIRCLE=0, no circle will be drawn. This special case is
primarily used to turn off the default unit-circle in vector plots.
- FLIP
-
switches the X and Y axes. It applies to the INITLOADINGS, LOADINGS, and PRELOADINGS plot-requests.
- NPLOT | NPLOTS=n
-
specifies the number of factors n ( ) to be plotted. It applies to the INITLOADINGS, LOADINGS, and PRELOADINGS plot-requests. Since this option can also be specified in the PROC FACTOR statement, the final value of n is determined by the following steps. The NPLOTS= value of the PROC FACTOR is read first. If the NPLOTS= option is specified
as a global-plot-option, the value of n will be updated. Then, if the NPLOTS= option is again specified in an individual plot-request, the value will be updated again for that individual plot-request. For example, in the following statement, four factors are extracted with the N=4 option:
) to be plotted. It applies to the INITLOADINGS, LOADINGS, and PRELOADINGS plot-requests. Since this option can also be specified in the PROC FACTOR statement, the final value of n is determined by the following steps. The NPLOTS= value of the PROC FACTOR is read first. If the NPLOTS= option is specified
as a global-plot-option, the value of n will be updated. Then, if the NPLOTS= option is again specified in an individual plot-request, the value will be updated again for that individual plot-request. For example, in the following statement, four factors are extracted with the N=4 option:
proc factor n=4 nplots=3 plots(nplots=4)=
(loadings preloadings(nplots=2));
Initially, plots of the first three factors are specified with the NPLOTS=3 option. When you are producing ODS graphical plots,
the global-plot-option NPLOTS=4 is used. As a result, the LOADINGS plot-request will produce plots for all pairs of the first 4 factors. However, because the NPLOTS=2 is specified locally for the PRELOADINGS
plot-request, it will produce a prerotated factor loading plot for the first two factors only.
The default NPLOTS= value is 5 or the total number of factors (m), whichever is smaller. If you specify an NPLOTS= value that is greater than m, NPLOTS=m will be used.
- PATHDIAGRAM
-
creates a path diagram for the last factor model. The last factor model refers to the initial factor solution if you do not
specify any rotations. It refers to the rotated factor solution if you use the ROTATE=
option. The path diagram shows the links between factors and variables, the factor correlations, and the error variances
in the model.
The path diagram does not display all non-zero directed links between factors and variables. It displays only those directed
links that have factor loading estimates at 0.3 or bigger in magnitude. PROC FACTOR uses this 0.3-criterion by default. You
can set your own criterion by using the FUZZ=
option in the PROC FACTOR statement.
If you use both the METHOD=
ML and SE
options in the PROC FACTOR statement, the statistical significance of the factor loading estimate is also required for displaying
the corresponding directed link between a variable and a factor. The default level of significance is 0.05. You can set your
own level of significance by using the ALPHA=
option in the PROC FACTOR statement.
Alternatively, you can produce path diagrams by using the the PATHDIAGRAM Statement
, which provides many options that enables you to create highly customized path diagrams.
- PLOTREF
-
plots the reference structures rather than the factor pattern loadings. It applies to the INITLOADINGS, LOADINGS, and PRELOADINGS
plot-requests when the factor solution is oblique. This option can also be set globally as an option in the PROC FACTOR statement.
- UNPACK
-
plots component graphs separately. It applies to the SCREE plot-request only.
- VECTOR
-
plots loadings in vector form. It applies to the INITLOADINGS, LOADINGS, and PRELOADINGS plot-requests when the factor solution is orthogonal. For oblique solutions, the VECTOR option is ignored and the default scatter plots
for factor loadings or reference structures are displayed.
Be aware that the PLOT
option in the PROC FACTOR statement requests only the printer plots of factor loadings. The current option PLOTS= or PLOT=,
however, is for ODS graphical plots.
You can specify options for the requested ODS graphical plots as global-plot-options or as local options. Global-plot-options apply to all appropriate individual plot-requests specified. For example, because the SCREE plot is not subject to axes flipping, the following two specifications are equivalent:
plots(flip)=(loadings preloadings scree)
plots=(loadings(flip) preloadings(flip) scree)
Options specified locally after each plot-request apply to that plot-request only. For example, consider the following specification:
plots=(scree(unpack) loadings(plotref) preloadings(flip))
The FLIP option applies to the PRELOADINGS plot-request but not the LOADINGS plot-request; the PLOTREF option applies to the LOADINGS plot-request but not the PRELOADINGS plot-request; and the UNPACK option applies to the SCREE plot-request only.
-
POWER=n
-
specifies the power to be used in computing the target pattern for the option ROTATE=
PROMAX. Valid values must be integers 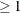 . The default value is 3. You can also specify the POWER= value in the ROTATE=
option—for example, ROTATE=
PROMAX(4).
. The default value is 3. You can also specify the POWER= value in the ROTATE=
option—for example, ROTATE=
PROMAX(4).
-
PREFIX=name
-
specifies a prefix for naming the factors. By default, the names are Factor1, Factor2, …, Factorn. If you specify PREFIX=ABC, the factors are named ABC1, ABC2, ABC3, and so on. The number of characters in the prefix plus
the number of digits required to designate the variables should not exceed the current name length defined by the VALIDVARNAME=
system option.
-
PREPLOT
-
plots the factor pattern before rotation. This option produces printer plots. High-quality ODS graphical plots for factor
patterns can be requested with the PLOTS=
PRELOADINGS option.
-
PREROTATE=name
PRE=name
-
specifies the prerotation method for the option ROTATE=
PROMAX. Any rotation method other than PROMAX or PROCRUSTES can be used. The default is PREROTATE=VARIMAX. If a previously
rotated pattern is read using the option METHOD=
PATTERN, you should specify the PREROTATE=NONE option.
-
PRINT
-
displays the input factor pattern or scoring coefficients and related statistics. In oblique cases, the reference and factor
structures are computed and displayed. The PRINT option is effective only with the option METHOD=
PATTERN or METHOD=
SCORE.
-
PRIORS=name
-
specifies a method for computing prior communality estimates. You can specify numeric values for the prior communality estimates
by using the PRIORS statement. Valid values for name are as follows:
- ASMC | A
-
sets the prior communality estimates proportional to the squared multiple correlations but adjusted so that their sum is equal
to that of the maximum absolute correlations (Cureton, 1968).
- INPUT | I
-
reads the prior communality estimates from the first observation with either _TYPE_=’PRIORS’ or _TYPE_=’COMMUNAL’ in the DATA=
data set (which cannot be TYPE=DATA).
- MAX | M
-
sets the prior communality estimate for each variable to its maximum absolute correlation with any other variable.
- ONE | O
-
sets all prior communalities to 1.0.
- RANDOM | R
-
sets the prior communality estimates to pseudo-random numbers uniformly distributed between 0 and 1.
- SMC | S
-
sets the prior communality estimate for each variable to its squared multiple correlation with all other variables.
The default prior communality estimates are as follows:
|
METHOD=
|
|
PRIORS=
|
|
PRINCIPAL
|
|
ONE
|
|
PRINIT
|
|
ONE
|
|
ALPHA
|
|
SMC
|
|
ULS
|
|
SMC
|
|
ML
|
|
SMC
|
|
HARRIS
|
|
(not applicable)
|
|
IMAGE
|
|
(not applicable)
|
|
PATTERN
|
|
(not applicable)
|
|
SCORE
|
|
(not applicable)
|
By default, the options METHOD=
PRINIT, METHOD=
ULS, METHOD=
ALPHA, and METHOD=
ML stop iterating and set the number of factors to 0 if an estimated communality exceeds 1. The options HEYWOOD
and ULTRAHEYWOOD
allow processing to continue.
-
PROPORTION=p
PERCENT=p
P=p
-
specifies the proportion of common variance to be accounted for by the retained factors. The proportion of common variance
is computed using the total prior communality estimates as the basis. If the value is greater than one, it is interpreted
as a percentage and divided by 100. The options PROPORTION=0.75 and PERCENT=75 are equivalent. The default value is 1.0 or
100%. You cannot specify the PROPORTION= option with the METHOD=
PATTERN or METHOD=
SCORE option. If you specify two or more of the PROPORTION=, NFACTORS=
, and MINEIGEN=
options, the number of factors retained is the minimum number satisfying any of the criteria.
-
RANDOM=n
-
specifies a positive integer as a starting value for the pseudo-random number generator for use with the option PRIORS=
RANDOM. If you do not specify the RANDOM= option, the time of day is used to initialize the pseudo-random number sequence.
Valid values must be integers 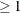 .
.
-
RCONVERGE=p
RCONV=p
-
specifies the convergence criterion value p (p 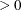 ) for rotation cycles. Rotation stops when the scaled change of the simplicity function value is less than p. Mathematically, the convergence criterion is
) for rotation cycles. Rotation stops when the scaled change of the simplicity function value is less than p. Mathematically, the convergence criterion is
where 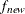 and
and 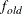 are simplicity function values of the current cycle and the previous cycle, respectively,
are simplicity function values of the current cycle and the previous cycle, respectively, 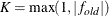 is a scaling factor, and p is 1E–9 by default.
is a scaling factor, and p is 1E–9 by default.
-
REORDER
RE
-
causes the rows (variables) of various factor matrices to be reordered on the output. Variables with their highest absolute
loading (reference structure loading for oblique rotations) on the first factor are displayed first, from largest to smallest
loading, followed by variables with their highest absolute loading on the second factor, and so on. The order of the variables
in the output data set is not affected. The factors are not reordered.
-
RESIDUALS
RES
-
displays the residual correlation matrix and the associated partial correlation matrix. The diagonal elements of the residual
correlation matrix are the unique variances.
-
RITER=n
-
specifies the maximum number of cycles n for factor rotation. Except for promax and Procrustes, you can use the RITER= option with all rotation methods. The default
n is the maximum between 10 times the number of variables and 100.
-
ROTATE=name
R=name
-
specifies the rotation method. The default is ROTATE=NONE.
Valid names for orthogonal rotations are as follows:
- BIQUARTIMAX | BIQMAX
-
specifies orthogonal biquartimax rotation. This corresponds to the specification ROTATE=ORTHOMAX(.5).
- EQUAMAX | E
-
specifies orthogonal equamax rotation. This corresponds to the specification ROTATE=ORTHOMAX with GAMMA=
number of factors/2.
- FACTORPARSIMAX | FPA
-
specifies orthogonal factor parsimax rotation. This corresponds to the specification ROTATE=ORTHOMAX with GAMMA=
number of variables.
- NONE | N
-
specifies that no rotation be performed, leaving the original orthogonal solution.
- ORTHCF(p1,p2) | ORCF(p1,p2)
-
specifies the orthogonal Crawford-Ferguson rotation with the weights p1 and p2 for variable parsimony and factor parsimony, respectively. See the definitions of weights in the section Simplicity Functions for Rotations.
- ORTHGENCF(p1,p2,p3,p4) | ORGENCF(p1,p2,p3,p4)
-
specifies the orthogonal generalized Crawford-Ferguson rotation with the four weights p1, p2, p3, and p4. See the definitions of weights in the section Simplicity Functions for Rotations.
- ORTHOMAX<(p)> | ORMAX<(p)>
-
specifies the orthomax rotation with orthomax weight p. If ROTATE=ORTHOMAX is used, the default p value is 1 unless specified otherwise in the GAMMA=
option. Alternatively, ROTATE=ORTHOMAX(p) specifies p as the orthomax weight or the GAMMA=
value. See the definition of the orthomax weight in the section Simplicity Functions for Rotations.
- PARSIMAX | PA
-
specifies orthogonal parsimax rotation. This corresponds to the specification ROTATE=ORTHOMAX with
where nvar is the number of variables and nfact is the number of factors.
- QUARTIMAX | QMAX | Q
-
specifies orthogonal quartimax rotation. This corresponds to the specification ROTATE=ORTHOMAX(0).
- VARIMAX | V
-
specifies orthogonal varimax rotation. This corresponds to the specification ROTATE=ORTHOMAX with GAMMA=
1.
Valid names for oblique rotations are as follows:
- BIQUARTIMIN | BIQMIN
-
specifies biquartimin rotation. It corresponds to the specification ROTATE=OBLIMIN(.5) or ROTATE=OBLIMIN with TAU=
0.5.
- COVARIMIN | CVMIN
-
specifies covarimin rotation. It corresponds to the specification ROTATE=OBLIMIN(1) or ROTATE=OBLIMIN with TAU=
1.
- HK<(p)> | H<(p)>
-
specifies Harris-Kaiser case II orthoblique rotation. When specifying this option, you can use the HKPOWER=
option to set the power of the square roots of the eigenvalues by which the eigenvectors are scaled, assuming that the factors
are extracted by the principal factor method. For other extraction methods, the unrotated factor pattern is column normalized.
The power is then applied to the column normalizing constants, instead of the eigenvalues. You can also use ROTATE=HK(p), with p representing the HKPOWER=
value. The default associated orthogonal rotation with ROTATE=HK is the varimax rotation without Kaiser normalization. You
might associate the Harris-Kaiser with other orthogonal rotations by using the ROTATE= option together with the HKPOWER=
option.
- OBBIQUARTIMAX | OBIQMAX
-
specifies oblique biquartimax rotation.
- OBEQUAMAX | OE
-
specifies oblique equamax rotation.
- OBFACTORPARSIMAX | OFPA
-
specifies oblique factor parsimax rotation.
- OBLICF(p1,p2) | OBCF(p1,p2)
-
specifies the oblique Crawford-Ferguson rotation with the weights p1 and p2 for variable parsimony and factor parsimony, respectively. See the definitions of weights in the section Simplicity Functions for Rotations.
- OBLIGENCF(p1,p2,p3,p4) | OBGENCF(p1,p2,p3,p4)
-
specifies the oblique generalized Crawford-Ferguson rotation with the four weights p1, p2, p3, and p4. See the definitions of weights in the section Simplicity Functions for Rotations.
- OBLIMIN<(p)> | OBMIN<(p)>
-
specifies the oblimin rotation with oblimin weight p. If ROTATE=OBLIMIN is used, the default p value is zero unless specified otherwise in the TAU=
option. Alternatively, ROTATE=OBLIMIN(p) specifies p as the oblimin weight or the TAU=
value. See the definition of the oblimin weight in the section Simplicity Functions for Rotations.
- OBPARSIMAX | OPA
-
specifies oblique parsimax rotation.
- OBQUARTIMAX | OQMAX
-
specifies oblique quartimax rotation. This is the same as the QUARTIMIN method.
- OBVARIMAX | OV
-
specifies oblique varimax rotation.
- PROCRUSTES
-
specifies oblique Procrustes rotation with the target pattern provided by the TARGET=
data set. The unrestricted least squares method is used with factors scaled to unit variance after rotation.
- PROMAX<(p)> | P<(p)>
-
specifies oblique promax rotation. You can use the PREROTATE=
option to set the desirable prerotation method, orthogonal or oblique. When used with ROTATE=PROMAX, the POWER=
option lets you specify the power for forming the target. You can also use ROTATE=PROMAX(p), where p represents the POWER=
value.
- QUARTIMIN | QMIN
-
specifies quartimin rotation. It is the same as the oblique quartimax method. It also corresponds to the specification ROTATE=OBLIMIN(0)
or ROTATE=OBLIMIN with TAU=
0.
-
ROUND
-
prints correlation and loading matrices with entries multiplied by 100 and rounded to the nearest integer. The exact values
can be obtained from the OUTSTAT=
and ODS output data sets. The ROUND option also flags absolute values larger than the FLAG=
value with an asterisk in correlation and loading matrices (see the FLAG=
option). If the FLAG=
option is not specified, the root mean square of all the values in the matrix printed is used as the default FLAG=
value. The ROUND option has no effect when standard errors or confidence intervals are also printed.
-
SCORE
-
displays the factor scoring coefficients. The squared multiple correlation of each factor with the variables is also displayed
except in the case of unrotated principal components. The SCORE option also outputs the factor scoring coefficients in the
_TYPE_=SCORE or _TYPE_=USCORE observations in the OUTSTAT= data set. Unless you specify the NOINT
option in PROC FACTOR, the scoring coefficients should be applied to standardized variables—variables that are centered by
subtracting the original variable means and then divided by the original variable standard deviations. With the NOINT
option, the scoring coefficients should be applied to data without centering.
-
SCREE
-
displays a scree plot of the eigenvalues (Cattell, 1966, 1978; Cattell and Vogelman, 1977; Horn and Engstrom, 1979). This option produces printer plots. High-quality scree plots can be requested with the PLOTS=
SCREE option.
-
SE
STDERR
-
computes standard errors for various classes of unrotated and rotated solutions under the maximum likelihood estimation.
-
SIMPLE
S
-
displays means, standard deviations, and the number of observations.
-
SINGULAR=p
SING=p
-
specifies the singularity criterion, where 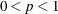 . The default value is 1E–8.
. The default value is 1E–8.
-
TARGET=SAS-data-set
-
specifies an input data set containing the target pattern for Procrustes rotation (see the description of the ROTATE=
option). The TARGET= data set must contain variables with the same names as those being factored. Each observation in the
TARGET= data set becomes one column of the target factor pattern. Missing values are treated as zeros. The _NAME_ and _TYPE_ variables are not required and are ignored if present.
-
TAU=p
-
specifies the oblimin weight used with the option ROTATE=
OBLIMIN or PREROTATE=
OBLIMIN. Alternatively, you can use ROTATE=
OBLIMIN(p) with p representing the oblimin weight. There is no restriction on valid values for the oblimin weight, although for practical purposes
a negative or zero value is recommended. The default TAU= value is 0, resulting in the quartimin rotation. See the section
Simplicity Functions for Rotations for more details.
-
ULTRAHEYWOOD
ULTRA
-
allows communalities to exceed 1. The ULTRAHEYWOOD option can cause convergence problems because communalities can become
extremely large, and ill-conditioned Hessians might occur. See the section Heywood Cases and Other Anomalies about Communality Estimates for a discussion of Heywood cases.
-
VARDEF=DF | N | WDF | WEIGHT | WGT
-
specifies the divisor used in the calculation of variances and covariances. The default value is VARDEF=DF. The values and
associated divisors are displayed in the following table where i=0 if the NOINT
option is used and i=1 otherwise, and where k is the number of partial variables specified in the PARTIAL statement.
|
Value
|
|
Description
|
|
Divisor
|
|
DF
|
|
degrees of freedom
|
|
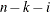
|
|
N
|
|
number of observations
|
|
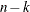
|
|
WDF
|
|
sum of weights DF
|
|
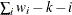
|
|
WEIGHT | WGT
|
|
sum of weights
|
|
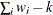
|
-
WEIGHT
-
factors a weighted correlation or covariance matrix. The WEIGHT option can be used only with the METHOD=
PRINCIPAL, METHOD=
PRINIT, METHOD=
ULS, or METHOD=
IMAGE option. The input data set must be of type CORR, UCORR, COV, UCOV, or FACTOR, and the variable weights are obtained
from an observation with _TYPE_=’WEIGHT’.


 Input Data SetOutput Data SetsConfidence Intervals and the Salience of Factor LoadingsSimplicity Functions for RotationsMissing ValuesCautionsFactor ScoresVariable Weights and Variance ExplainedHeywood Cases and Other Anomalies about Communality EstimatesTime RequirementsDisplayed OutputODS Table NamesODS Graphics
Input Data SetOutput Data SetsConfidence Intervals and the Salience of Factor LoadingsSimplicity Functions for RotationsMissing ValuesCautionsFactor ScoresVariable Weights and Variance ExplainedHeywood Cases and Other Anomalies about Communality EstimatesTime RequirementsDisplayed OutputODS Table NamesODS Graphics