The VARIOGRAM Procedure
The basic starting point in computing the empirical semivariance is the enumeration of pairs of points for the spatial data.
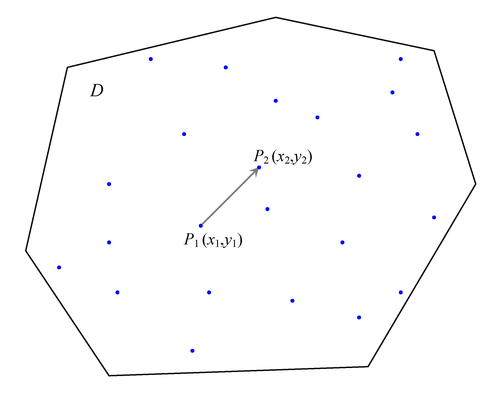
Figure 106.19 shows the spatial domain D and the set of n measurements ![]() ,
, ![]() , that have been sampled at the indicated locations in D. Two data points
, that have been sampled at the indicated locations in D. Two data points ![]() and
and ![]() , with coordinates
, with coordinates ![]() and
and ![]() , respectively, are selected for illustration.
, respectively, are selected for illustration.
A vector, or directed line segment, is drawn between these points. If the length
of this vector is smaller than the specified DEPSILON= value, then the pair is excluded from the continuity measure calculations because the two points ![]() and
and ![]() are considered to be at zero distance apart (or collocated). Spatial collocation might appear due to different scales in sampling, observations made at the same spatial location at
different time instances, and errors in the data sets. PROC VARIOGRAM excludes such pairs from the pairwise distance and semivariance
computations because they can cause numeric problems in spatial analysis.
are considered to be at zero distance apart (or collocated). Spatial collocation might appear due to different scales in sampling, observations made at the same spatial location at
different time instances, and errors in the data sets. PROC VARIOGRAM excludes such pairs from the pairwise distance and semivariance
computations because they can cause numeric problems in spatial analysis.
If this pair is not discarded on the basis of collocation, it is then classified—first by orientation of the directed line
segment ![]() , and then by its length
, and then by its length ![]() . For example, it is unlikely for actual data that the distance
. For example, it is unlikely for actual data that the distance ![]() between any pair of data points
between any pair of data points ![]() and
and ![]() located at
located at ![]() and
and ![]() , respectively, would exactly satisfy
, respectively, would exactly satisfy ![]() in the preceding computation of
in the preceding computation of ![]() . A similar argument can be made for the orientation of the segment
. A similar argument can be made for the orientation of the segment ![]() . Consequently, the pair
. Consequently, the pair ![]() is placed into an angle and distance class.
is placed into an angle and distance class.
The following subsections give more details about the nature of these classifications. You can also find extensive discussions about the size and the number of classes to consider for the computation of the empirical semivariogram.