The TTEST Procedure
When it is not feasible to assume that two groups of data are independent, and a natural pairing of the data exists, it is advantageous to use an analysis that takes the correlation into account. Using this correlation results in higher power to detect existing differences between the means. The differences between paired observations are assumed to be normally distributed. Some examples of this natural pairing are as follows:
-
pre- and post-test scores for a student receiving tutoring
-
fuel efficiency readings of two fuel types observed on the same automobile
-
sunburn scores for two sunblock lotions, one applied to the individual’s right arm, one to the left arm
-
political attitude scores of husbands and wives
In this example, taken from the SUGI Supplemental Library User’s Guide, Version 5 Edition, a stimulus is being examined to determine its effect on systolic blood pressure. Twelve men participate in the study. Each man’s systolic blood pressure is measured both before and after the stimulus is applied. The following statements input the data:
data pressure; input SBPbefore SBPafter @@; datalines; 120 128 124 131 130 131 118 127 140 132 128 125 140 141 135 137 126 118 130 132 126 129 127 135 ;
The variables SBPbefore and SBPafter denote the systolic blood pressure before and after the stimulus, respectively.
The statements to perform the test follow:
ods graphics on; proc ttest; paired SBPbefore*SBPafter; run; ods graphics off;
The PAIRED statement is used to test whether the mean change in systolic blood pressure is significantly different from zero. The tabular output is displayed in Output 103.3.1.
Output 103.3.1: TTEST Results
| N | Mean | Std Dev | Std Err | Minimum | Maximum |
|---|---|---|---|---|---|
| 12 | -1.8333 | 5.8284 | 1.6825 | -9.0000 | 8.0000 |
| Mean | 95% CL Mean | Std Dev | 95% CL Std Dev | ||
|---|---|---|---|---|---|
| -1.8333 | -5.5365 | 1.8698 | 5.8284 | 4.1288 | 9.8958 |
| DF | t Value | Pr > |t| |
|---|---|---|
| 11 | -1.09 | 0.2992 |
The variables SBPbefore and SBPafter are the paired variables with a sample size of 12. The summary statistics of the difference are displayed (mean, standard
deviation, and standard error) along with their confidence limits. The minimum and maximum differences are also displayed.
The t test is not significant (t = –1.09, p = 0.2992), indicating that the stimuli did not significantly affect systolic blood pressure.
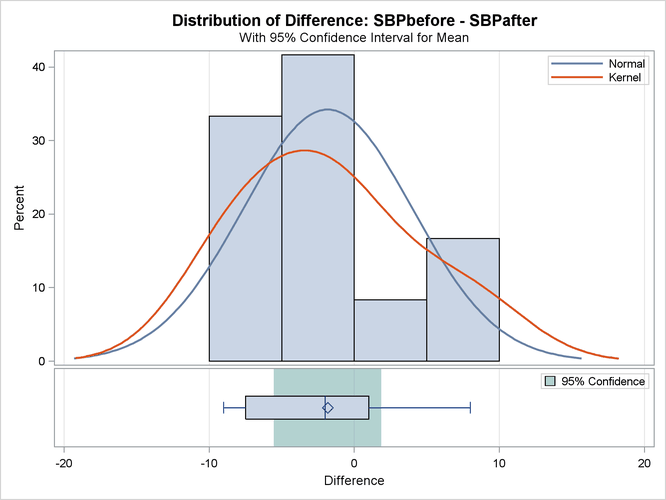
The summary panel in Output 103.3.2 shows a histogram, normal and kernel densities, box plot, and ![]() confidence interval of the
confidence interval of the SBPbefore – SBPafter difference.
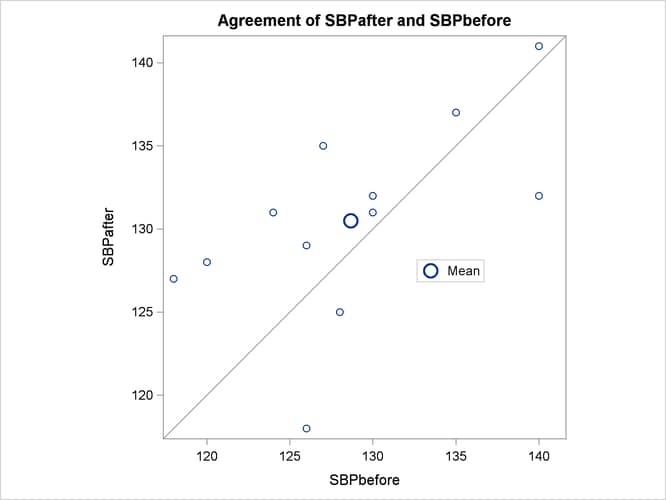
The agreement plot in Output 103.3.3 reveals that only three men have higher blood pressure before the stimulus than after.
But the differences for these men are relatively large, keeping the mean difference only slightly negative.
The profiles plot in Output 103.3.4 is a different view of the same information contained in Output 103.3.3, plotting the blood pressure from before to after the stimulus.
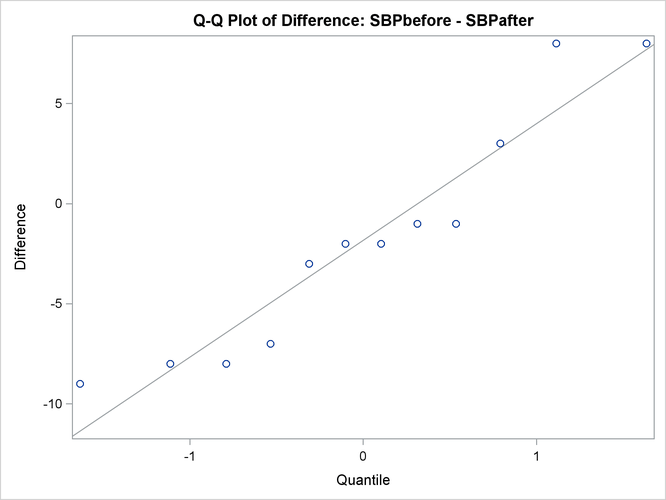
The Q-Q plot in Output 103.3.5 assesses the normality assumption.
The Q-Q plot shows no obvious deviations from normality. You can check the assumption of normality more rigorously by using PROC UNIVARIATE with the NORMAL option.