The SURVEYLOGISTIC Procedure
- Overview
- Getting Started
-
Syntax
 PROC SURVEYLOGISTIC StatementBY StatementCLASS StatementCLUSTER StatementCONTRAST StatementDOMAIN StatementEFFECT StatementESTIMATE StatementFREQ StatementLSMEANS StatementLSMESTIMATE StatementMODEL StatementOUTPUT StatementREPWEIGHTS StatementSLICE StatementSTORE StatementSTRATA StatementTEST StatementUNITS StatementWEIGHT Statement
PROC SURVEYLOGISTIC StatementBY StatementCLASS StatementCLUSTER StatementCONTRAST StatementDOMAIN StatementEFFECT StatementESTIMATE StatementFREQ StatementLSMEANS StatementLSMESTIMATE StatementMODEL StatementOUTPUT StatementREPWEIGHTS StatementSLICE StatementSTORE StatementSTRATA StatementTEST StatementUNITS StatementWEIGHT Statement -
Details
 Missing ValuesModel SpecificationModel FittingSurvey Design InformationLogistic Regression Models and ParametersVariance EstimationDomain AnalysisHypothesis Testing and EstimationLinear Predictor, Predicted Probability, and Confidence LimitsOutput Data SetsDisplayed OutputODS Table NamesODS Graphics
Missing ValuesModel SpecificationModel FittingSurvey Design InformationLogistic Regression Models and ParametersVariance EstimationDomain AnalysisHypothesis Testing and EstimationLinear Predictor, Predicted Probability, and Confidence LimitsOutput Data SetsDisplayed OutputODS Table NamesODS Graphics -
Examples

- References
The likelihood equation for a logistic regression model does not always have a finite solution. Sometimes there is a nonunique maximum on the boundary of the parameter space, at infinity. The existence, finiteness, and uniqueness of pseudo-estimates for the logistic regression model depend on the patterns of data points in the observation space (Albert and Anderson, 1984; Santner and Duffy, 1986).
Consider a binary response model. Let ![]() be the response of the ith subject, and let
be the response of the ith subject, and let ![]() be the row vector of explanatory variables (including the constant 1 associated with the intercept). There are three mutually
exclusive and exhaustive types of data configurations: complete separation, quasi-complete separation, and overlap.
be the row vector of explanatory variables (including the constant 1 associated with the intercept). There are three mutually
exclusive and exhaustive types of data configurations: complete separation, quasi-complete separation, and overlap.
- Complete separation
-
There is a complete separation of data points if there exists a vector
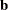 that correctly allocates all observations to their response groups; that is,
that correctly allocates all observations to their response groups; that is,
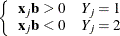
This configuration gives nonunique infinite estimates. If the iterative process of maximizing the likelihood function is allowed to continue, the log likelihood diminishes to zero, and the dispersion matrix becomes unbounded.
- Quasi-complete separation
-
The data are not completely separable, but there is a vector
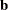 such that
such that
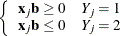
and equality holds for at least one subject in each response group. This configuration also yields nonunique infinite estimates. If the iterative process of maximizing the likelihood function is allowed to continue, the dispersion matrix becomes unbounded and the log likelihood diminishes to a nonzero constant.
- Overlap
-
If neither complete nor quasi-complete separation exists in the sample points, there is an overlap of sample points. In this configuration, the pseudo-estimates exist and are unique.
Complete separation and quasi-complete separation are problems typically encountered with small data sets. Although complete separation can occur with any type of data, quasi-complete separation is not likely with truly continuous explanatory variables.
The SURVEYLOGISTIC procedure uses a simple empirical approach to recognize the data configurations that lead to infinite parameter
estimates. The basis of this approach is that any convergence method of maximizing the log likelihood must yield a solution
that gives complete separation, if such a solution exists. In maximizing the log likelihood, there is no checking for complete
or quasi-complete separation if convergence is attained in eight or fewer iterations. Subsequent to the eighth iteration,
the probability of the observed response is computed for each observation. If the probability of the observed response is
one for all observations, there is a complete separation of data points and the iteration process is stopped. If the complete
separation of data has not been determined and an observation is identified to have an extremely large probability (![]() 0.95) of the observed response, there are two possible situations. First, there is overlap in the data set, and the observation
is an atypical observation of its own group. The iterative process, if allowed to continue, stops when a maximum is reached.
Second, there is quasi-complete separation in the data set, and the asymptotic dispersion matrix is unbounded. If any of the
diagonal elements of the dispersion matrix for the standardized observations vectors (all explanatory variables standardized
to zero mean and unit variance) exceeds 5,000, quasi-complete separation is declared and the iterative process is stopped.
If either complete separation or quasi-complete separation is detected, a warning message is displayed in the procedure output.
0.95) of the observed response, there are two possible situations. First, there is overlap in the data set, and the observation
is an atypical observation of its own group. The iterative process, if allowed to continue, stops when a maximum is reached.
Second, there is quasi-complete separation in the data set, and the asymptotic dispersion matrix is unbounded. If any of the
diagonal elements of the dispersion matrix for the standardized observations vectors (all explanatory variables standardized
to zero mean and unit variance) exceeds 5,000, quasi-complete separation is declared and the iterative process is stopped.
If either complete separation or quasi-complete separation is detected, a warning message is displayed in the procedure output.
Checking for quasi-complete separation is less foolproof than checking for complete separation. The NOCHECK option in the MODEL statement turns off the process of checking for infinite parameter estimates. In cases of complete or quasi-complete separation, turning off the checking process typically results in the procedure failing to converge.