The SURVEYLOGISTIC Procedure
- Overview
- Getting Started
-
Syntax
 PROC SURVEYLOGISTIC StatementBY StatementCLASS StatementCLUSTER StatementCONTRAST StatementDOMAIN StatementEFFECT StatementESTIMATE StatementFREQ StatementLSMEANS StatementLSMESTIMATE StatementMODEL StatementOUTPUT StatementREPWEIGHTS StatementSLICE StatementSTORE StatementSTRATA StatementTEST StatementUNITS StatementWEIGHT Statement
PROC SURVEYLOGISTIC StatementBY StatementCLASS StatementCLUSTER StatementCONTRAST StatementDOMAIN StatementEFFECT StatementESTIMATE StatementFREQ StatementLSMEANS StatementLSMESTIMATE StatementMODEL StatementOUTPUT StatementREPWEIGHTS StatementSLICE StatementSTORE StatementSTRATA StatementTEST StatementUNITS StatementWEIGHT Statement -
Details
 Missing ValuesModel SpecificationModel FittingSurvey Design InformationLogistic Regression Models and ParametersVariance EstimationDomain AnalysisHypothesis Testing and EstimationLinear Predictor, Predicted Probability, and Confidence LimitsOutput Data SetsDisplayed OutputODS Table NamesODS Graphics
Missing ValuesModel SpecificationModel FittingSurvey Design InformationLogistic Regression Models and ParametersVariance EstimationDomain AnalysisHypothesis Testing and EstimationLinear Predictor, Predicted Probability, and Confidence LimitsOutput Data SetsDisplayed OutputODS Table NamesODS Graphics -
Examples

- References
Four link functions are available in the SURVEYLOGISTIC procedure. The logit function is the default. To specify a different link function, use the LINK= option in the MODEL statement. The link functions and the corresponding distributions are as follows:
-
The logit function
![\[ g(p)=\log \left( \frac{p}{1-p} \right) \]](images/statug_surveylogistic0101.png)
is the inverse of the cumulative logistic distribution function, which is
![\[ F(x)=\frac{1}{1+e^{-x}} \]](images/statug_surveylogistic0102.png)
-
The probit (or normit) function
![\[ g(p)=\Phi ^{-1}(p) \]](images/statug_surveylogistic0103.png)
is the inverse of the cumulative standard normal distribution function, which is
![\[ F(x)=\Phi (x)=\frac{1}{\sqrt {2\pi }}\int _{-\infty }^ x e^{-\frac{1}{2} z^2} dz \]](images/statug_surveylogistic0104.png)
Traditionally, the probit function includes an additive constant 5, but throughout PROC SURVEYLOGISTIC, the terms probit and normit are used interchangeably, previously defined as
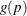 .
.
-
The complementary log-log function
![\[ g(p)=\log (-\log (1-p)) \]](images/statug_surveylogistic0106.png)
is the inverse of the cumulative extreme-value function (also called the Gompertz distribution), which is
![\[ F(x)=1-e^{-e^ x} \]](images/statug_surveylogistic0107.png)
-
The generalized logit function extends the binary logit link to a vector of levels
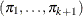 by contrasting each level with a fixed level
by contrasting each level with a fixed level
![\[ g(\pi _ i)=\log \left( \frac{\pi _ i}{\pi _{k+1}} \right) \quad i=1,\ldots , k \]](images/statug_surveylogistic0109.png)
The variances of the normal, logistic, and extreme-value distributions are not the same. Their respective means and variances are
|
Distribution |
Mean |
Variance |
|---|---|---|
|
Normal |
0 |
1 |
|
Logistic |
0 |
|
|
Extreme-value |
|
|
where ![]() is the Euler constant. In comparing parameter estimates that use different link functions, you need to take into account
the different scalings of the corresponding distributions and, for the complementary log-log function, a possible shift in
location. For example, if the fitted probabilities are in the neighborhood of 0.1 to 0.9, then the parameter estimates from
using the logit link function should be about
is the Euler constant. In comparing parameter estimates that use different link functions, you need to take into account
the different scalings of the corresponding distributions and, for the complementary log-log function, a possible shift in
location. For example, if the fitted probabilities are in the neighborhood of 0.1 to 0.9, then the parameter estimates from
using the logit link function should be about ![]() larger than the estimates from the probit link function.
larger than the estimates from the probit link function.