The QUANTREG Procedure
Quantile regression is used extensively in ecological studies (Cade and Noon, 2003). Recently, Dunham, Cade, and Terrell (2002) applied quantile regression to analyze fish-habitat relationships for Lahontan cutthroat trout in 13 streams of the eastern Lahontan basin, which covers most of northern Nevada and parts of southern Oregon. The density of trout (number of trout per meter) was measured by sampling stream sites from 1993 to 1999. The width-to-depth ratio of the stream site was determined as a measure of stream habitat.
The goal of this study was to explore the relationship between the conditional quantiles of trout density and the width-to-depth ratio. The scatter plot of the data in Figure 81.1 indicates a nonlinear relationship, so it is reasonable to fit regression models for the conditional quantiles of the log of density. Because regression quantiles are equivariant under any monotonic (linear or nonlinear) transformation (Koenker and Hallock, 2001), the exponential transformation converts the conditional quantiles to the original density scale.
The data set trout, which follows, includes the average numbers of Lahontan cutthroat trout per meter of stream (Density), the logarithm of Density (LnDensity), and the width-to-depth ratios (WDRatio) for 71 samples:
data trout; input Density WDRatio LnDensity @@; datalines; 0.38732 8.6819 -0.94850 1.16956 10.5102 0.15662 0.42025 10.7636 -0.86690 0.50059 12.7884 -0.69197 0.74235 12.9266 -0.29793 0.40385 14.4884 -0.90672 0.35245 15.2476 -1.04284 0.11499 16.6495 -2.16289 0.18290 16.7188 -1.69881 0.06619 16.7859 -2.71523 0.70330 19.0141 -0.35197 0.50845 19.0548 -0.67639 ... more lines ... 0.25125 54.6916 -1.38129 ;
The following statements use the QUANTREG procedure to fit a simple linear model for the 50th and 90th percentiles of LnDensity:
ods graphics on;
proc quantreg data=trout alpha=0.1 ci=resampling;
model LnDensity = WDRatio / quantile=0.5 0.9
CovB seed=1268;
test WDRatio / wald lr;
run;
The MODEL statement specifies a simple linear regression model with LnDensity as the response variable Y and WDRatio as the covariate X. The QUANTILE= option requests that the regression quantile function ![]() be estimated by solving the following equation, where
be estimated by solving the following equation, where ![]() :
:
By default, the regression coefficients ![]() are estimated by using the simplex algorithm, which is explained in the section Simplex Algorithm. The ALPHA= option requests 90% confidence limits for the regression parameters, and the option CI=RESAMPLING specifies that
the intervals be computed by using the Markov chain marginal bootstrap (MCMB) resampling method of He and Hu (2002). When you specify the CI=RESAMPLING option, the QUANTREG procedure also computes standard errors, t values, and p-values of regression parameters by using the MCMB resampling method. The SEED= option specifies a seed for the resampling
method. The COVB option requests covariance matrices for the estimated regression coefficients, and the TEST statement requests
tests for the hypothesis that the slope parameter (the coefficient of
are estimated by using the simplex algorithm, which is explained in the section Simplex Algorithm. The ALPHA= option requests 90% confidence limits for the regression parameters, and the option CI=RESAMPLING specifies that
the intervals be computed by using the Markov chain marginal bootstrap (MCMB) resampling method of He and Hu (2002). When you specify the CI=RESAMPLING option, the QUANTREG procedure also computes standard errors, t values, and p-values of regression parameters by using the MCMB resampling method. The SEED= option specifies a seed for the resampling
method. The COVB option requests covariance matrices for the estimated regression coefficients, and the TEST statement requests
tests for the hypothesis that the slope parameter (the coefficient of WDRatio) is 0.
Figure 81.3 displays model information and summary statistics for the variables in the model. The summary statistics include the median and the standardized median absolute deviation (MAD), which are robust measures of univariate location and scale, respectively. For more information about the standardized MAD, see Huber (1981, p. 108).
Figure 81.3: Model Fitting Information and Summary Statistics
| Model Information | |
|---|---|
| Data Set | WORK.TROUT |
| Dependent Variable | LnDensity |
| Number of Independent Variables | 1 |
| Number of Observations | 71 |
| Optimization Algorithm | Simplex |
| Method for Confidence Limits | Resampling |
| Summary Statistics | ||||||
|---|---|---|---|---|---|---|
| Variable | Q1 | Median | Q3 | Mean | Standard Deviation |
MAD |
| WDRatio | 22.0917 | 29.4083 | 35.9382 | 29.1752 | 9.9859 | 10.4970 |
| LnDensity | -2.0511 | -1.3813 | -0.8669 | -1.4973 | 0.7682 | 0.8214 |
Figure 81.4 and Figure 81.5 display the parameter estimates, standard errors, 95% confidence limits, t values, and p-values that are computed by the resampling method.
Figure 81.4: Parameter Estimates at QUANTILE=0.5
| Parameter Estimates | |||||||
|---|---|---|---|---|---|---|---|
| Parameter | DF | Estimate | Standard Error | 90% Confidence Limits | t Value | Pr > |t| | |
| Intercept | 1 | -0.9811 | 0.3952 | -1.6400 | -0.3222 | -2.48 | 0.0155 |
| WDRatio | 1 | -0.0136 | 0.0123 | -0.0341 | 0.0068 | -1.11 | 0.2705 |
Figure 81.5: Parameter Estimates at QUANTILE=0.9
| Parameter Estimates | |||||||
|---|---|---|---|---|---|---|---|
| Parameter | DF | Estimate | Standard Error | 90% Confidence Limits | t Value | Pr > |t| | |
| Intercept | 1 | 0.0576 | 0.2606 | -0.3769 | 0.4921 | 0.22 | 0.8257 |
| WDRatio | 1 | -0.0215 | 0.0075 | -0.0340 | -0.0091 | -2.88 | 0.0053 |
The 90th percentile of trout density can be predicted from the width-to-depth ratio as follows:
This is the upper dashed curve that is plotted in Figure 81.1. The lower dashed curve for the median can be obtained in a similar fashion.
The covariance matrices for the estimated parameters are shown in Figure 81.6. The resampling method that is used for the confidence intervals is also used to compute these matrices.
Figure 81.6: Covariance Matrices of the Estimated Parameters
| Estimated Covariance Matrix for Quantile Level = 0.5 |
||
|---|---|---|
| Intercept | WDRatio | |
| Intercept | 0.156191 | -.004653 |
| WDRatio | -.004653 | 0.000151 |
| Estimated Covariance Matrix for Quantile Level = 0.9 |
||
|---|---|---|
| Intercept | WDRatio | |
| Intercept | 0.067914 | -.001877 |
| WDRatio | -.001877 | 0.000056 |
The tests requested by the TEST statement are shown in Figure 81.7. Both the Wald test and the likelihood ratio test indicate that the coefficient of width-to-depth ratio is significantly different from 0 at the 90th percentile, but the difference is not significant at the median.
Figure 81.7: Tests of Significance
| Test Results | |||||
|---|---|---|---|---|---|
| Quantile Level |
Test | Test Statistic | DF | Chi-Square | Pr > ChiSq |
| 0.5 | Wald | 1.2339 | 1 | 1.23 | 0.2666 |
| 0.5 | Likelihood Ratio | 1.1467 | 1 | 1.15 | 0.2842 |
| 0.9 | Wald | 8.3031 | 1 | 8.30 | 0.0040 |
| 0.9 | Likelihood Ratio | 9.0529 | 1 | 9.05 | 0.0026 |
In many quantile regression problems it is useful to examine how the estimated regression parameters for each covariate change
as a function of ![]() in the interval
in the interval ![]() . The following statements use the QUANTREG procedure to request the estimated quantile processes
. The following statements use the QUANTREG procedure to request the estimated quantile processes ![]() for the slope and intercept parameters:
for the slope and intercept parameters:
proc quantreg data=trout alpha=0.1 ci=resampling;
model LnDensity = WDRatio / quantile=process seed=1268
plot=quantplot;
run;
The QUANTILE=PROCESS option requests an estimate of the quantile process for each regression parameter. The options ALPHA=0.1 and CI=RESAMPLING specify that 90% confidence bands for the quantile processes be computed by using the resampling method.
Figure 81.8 displays a portion of the objective function table for the entire quantile process. The objective function is evaluated at
77 values of ![]() in the interval
in the interval ![]() . The table also provides predicted values of the conditional quantile function
. The table also provides predicted values of the conditional quantile function ![]() at the mean for
at the mean for WDRatio, which can be used to estimate the conditional density function.
Figure 81.8: Objective Function
| Objective Function for Quantile Process |
|||
|---|---|---|---|
| Label | Quantile Level |
Objective Function |
Predicted at Mean |
| t0 | 0.005634 | 0.7044 | -3.2582 |
| t1 | 0.020260 | 2.5331 | -3.0331 |
| t2 | 0.031348 | 3.7421 | -2.9376 |
| t3 | 0.046131 | 5.2538 | -2.7013 |
| . | . | . | . |
| . | . | . | . |
| . | . | . | . |
| t73 | 0.945705 | 4.1433 | -0.4361 |
| t74 | 0.966377 | 2.5858 | -0.4287 |
| t75 | 0.976060 | 1.8512 | -0.4082 |
| t76 | 0.994366 | 0.4356 | -0.4082 |
Figure 81.9 displays a portion of the table of the quantile processes for the estimated parameters and confidence limits.
Figure 81.9: Objective Function
| Parameter Estimates for Quantile Process | |||
|---|---|---|---|
| Label | Quantile | Intercept | WDRatio |
| . | . | . | . |
| . | . | . | . |
| . | . | . | . |
| t57 | 0.765705 | -0.42205 | -0.01335 |
| lower90 | 0.765705 | -0.91952 | -0.02682 |
| upper90 | 0.765705 | 0.07541 | 0.00012 |
| t58 | 0.786206 | -0.32688 | -0.01592 |
| lower90 | 0.786206 | -0.80883 | -0.02895 |
| upper90 | 0.786206 | 0.15507 | -0.00289 |
| . | . | . | . |
| . | . | . | . |
| . | . | . | . |
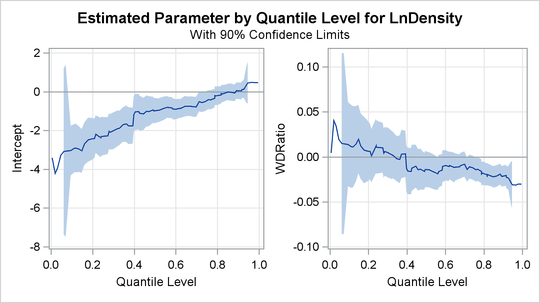
When ODS Graphics is enabled, the PLOT=QUANTPLOT option in the MODEL statement requests a plot of the estimated quantile processes.
For more information about enabling and disabling ODS Graphics, see the section Enabling and Disabling ODS Graphics in Chapter 21: Statistical Graphics Using ODS.
The left side of Figure 81.10 displays the process for the intercept, and the right side displays the process for the coefficient of WDRatio.
The process plot for WDRatio shows that the slope parameter changes from positive to negative as the quantile increases and that it changes sign with
a sharp drop at the 40th percentile. The 90% confidence bands show that the relationship between LnDensity and WDRatio (expressed by the slope) is not significant below the 78th percentile. This situation can also be seen in Figure 81.9, which shows that 0 falls between the lower and upper confidence limits of the slope parameter for quantiles below 0.78.
Since the confidence intervals for the extreme quantiles are not stable because of insufficient data, the confidence band
is not displayed outside the interval (0.05, 0.95).