The POWER Procedure

MULTREG Statement

Subsections:

Summary of Options
Dictionary of Options
Restrictions on Option Combinations
Option Groups for Common Analyses

MULTREG <options> ;

The MULTREG statement performs power and sample size analyses for Type III F tests of sets of predictors in multiple linear regression, assuming either fixed or normally distributed predictors.

Summary of Options

Table 75.4 summarizes the options available in the MULTREG statement.

Table 75.4: MULTREG Statement Options

Option	Description
Define analysis
TEST=	Specifies the statistical analysis
Specify analysis information
ALPHA=	Specifies the significance level
MODEL=	Specifies the assumed distribution of the predictors
NFULLPREDICTORS=	Specifies the number of predictors in the full model
NOINT	Specifies a no-intercept model
NREDUCEDPREDICTORS=	Specifies the number of predictors in the reduced model
NTESTPREDICTORS=	Specifies the number of predictors being tested
Specify effects
PARTIALCORR=	Specifies the partial correlation
RSQUAREDIFF=	Specifies the difference in $R^2$
RSQUAREFULL=	Specifies the $R^2$ of the full model
RSQUAREREDUCED=	Specifies the $R^2$ of the reduced model
Specify sample size
NFRACTIONAL	Enables fractional input and output for sample sizes
NTOTAL=	Specifies the sample size
Specify power
POWER=	Specifies the desired power
Control ordering in output
OUTPUTORDER=	Controls the order of parameters

Table 75.5 summarizes the valid result parameters in the MULTREG statement.

Table 75.5: Summary of Result Parameters in the MULTREG Statement

Analyses	Solve For	Syntax
TEST=TYPE3	Power	POWER=.
	Sample size	NTOTAL=.

Dictionary of Options

ALPHA=number-list

specifies the level of significance of the statistical test. The default is 0.05, corresponding to the usual 0.05 $\times$ 100% = 5% level of significance. For information about specifying the number-list, see the section Specifying Value Lists in Analysis Statements.

MODEL=keyword-list

specifies the assumed distribution of the tested predictors. MODEL=FIXED indicates a fixed predictor distribution. MODEL=RANDOM (the default) indicates a joint multivariate normal distribution for the response and tested predictors. You can use the aliases CONDITIONAL for FIXED and UNCONDITIONAL for RANDOM. For information about specifying the keyword-list, see the section Specifying Value Lists in Analysis Statements.

FIXED: fixed predictors
RANDOM: random (multivariate normal) predictors

NFRACTIONAL NFRAC

enables fractional input and output for sample sizes. See the section Sample Size Adjustment Options for information about the ramifications of the presence (and absence) of the NFRACTIONAL option.

NFULLPREDICTORS=number-list NFULLPRED=number-list

specifies the number of predictors in the full model, not counting the intercept. For information about specifying the number-list, see the section Specifying Value Lists in Analysis Statements.

NOINT

specifies a no-intercept model (for both full and reduced models). By default, the intercept is included in the model. If you want to test the intercept, you can specify the NOINT option and simply consider the intercept to be one of the predictors being tested. For information about specifying the number-list, see the section Specifying Value Lists in Analysis Statements.

NREDUCEDPREDICTORS=number-list NREDUCEDPRED=number-list NREDPRED=number-list

specifies the number of predictors in the reduced model, not counting the intercept. This is the same as the difference between values of the NFULLPREDICTORS= and NTESTPREDICTORS= options. Note that supplying a value of 0 is the same as specifying an F test of a Pearson correlation. This option cannot be used at the same time as the NTESTPREDICTORS= option. For information about specifying the number-list, see the section Specifying Value Lists in Analysis Statements.

NTESTPREDICTORS=number-list NTESTPRED=number-list

specifies the number of predictors being tested. This is the same as the difference between values of the NFULLPREDICTORS= and NREDUCEDPREDICTORS= options. Note that supplying identical values for the NTESTPREDICTORS= and NFULLPREDICTORS= options is the same as specifying an F test of a Pearson correlation. This option cannot be used at the same time as the NREDUCEDPREDICTORS= option. For information about specifying the number-list, see the section Specifying Value Lists in Analysis Statements.

NTOTAL=number-list

specifies the sample size or requests a solution for the sample size with a missing value (NTOTAL=.). The minimum acceptable value for the sample size depends on the MODEL=, NOINT, NFULLPREDICTORS=, NTESTPREDICTORS=, and NREDUCEDPREDICTORS= options. It ranges from p + 1 to p + 3, where p is the value of the NFULLPREDICTORS option. For further information about minimum NTOTAL values, see Table 75.30. For information about specifying the number-list, see the section Specifying Value Lists in Analysis Statements.

OUTPUTORDER=INTERNAL | REVERSE | SYNTAX

controls how the input and default analysis parameters are ordered in the output. OUTPUTORDER=INTERNAL (the default) arranges the parameters in the output according to the following order of their corresponding options:

MODEL=
NFULLPREDICTORS=
NTESTPREDICTORS=
NREDUCEDPREDICTORS=
ALPHA=
PARTIALCORR=
RSQUAREFULL=
RSQUAREREDUCED=
RSQUAREDIFF=
NTOTAL=
POWER=

The OUTPUTORDER=SYNTAX option arranges the parameters in the output in the same order in which their corresponding options are specified in the MULTREG statement. The OUTPUTORDER=REVERSE option arranges the parameters in the output in the reverse of the order in which their corresponding options are specified in the MULTREG statement.

PARTIALCORR=number-list PCORR=number-list

specifies the partial correlation between the tested predictors and the response, adjusting for any other predictors in the model. For information about specifying the number-list, see the section Specifying Value Lists in Analysis Statements.

POWER=number-list

specifies the desired power of the test or requests a solution for the power with a missing value (POWER=.). The power is expressed as a probability, a number between 0 and 1, rather than as a percentage. For information about specifying the number-list, see the section Specifying Value Lists in Analysis Statements.

RSQUAREDIFF=number-list RSQDIFF=number-list

specifies the difference in $R^2$ between the full and reduced models. This is equivalent to the proportion of variation explained by the predictors you are testing. It is also equivalent to the squared semipartial correlation of the tested predictors with the response. For information about specifying the number-list, see the section Specifying Value Lists in Analysis Statements.

RSQUAREFULL=number-list RSQFULL=number-list

specifies the $R^2$ of the full model, where $R^2$ is the proportion of variation explained by the model. For information about specifying the number-list, see the section Specifying Value Lists in Analysis Statements.

RSQUAREREDUCED=number-list RSQREDUCED=number-list RSQRED=number-list

specifies the $R^2$ of the reduced model, where $R^2$ is the proportion of variation explained by the model. If the reduced model is an empty or intercept-only model (in other words, if NREDUCEDPREDICTORS=0 or NTESTPREDICTORS=NFULLPREDICTORS), then RSQUAREREDUCED=0 is assumed. For information about specifying the number-list, see the section Specifying Value Lists in Analysis Statements.

TEST=TYPE3

specifies a Type III F test of a set of predictors adjusting for any other predictors in the model. This is the default test option.

Restrictions on Option Combinations

To specify the number of predictors, use any two of these three options:

the number of predictors in the full model (NFULLPREDICTORS=)
the number of predictors in the reduced model (NREDUCEDPREDICTORS=)
the number of predictors being tested (NTESTPREDICTORS=)

To specify the effect, choose one of the following parameterizations:

partial correlation (by using the PARTIALCORR= option)
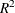$R^2$ for the full and reduced models (by using any two of RSQUAREDIFF=, RSQUAREFULL=, and RSQUAREREDUCED=)

Option Groups for Common Analyses

This section summarizes the syntax for the common analyses supported in the MULTREG statement.

Type III F Test of a Set of Predictors

You can express effects in terms of partial correlation, as in the following statements. Default values of the TEST=, MODEL=, and ALPHA= options specify a Type III F test with a significance level of 0.05, assuming normally distributed predictors.

proc power;
   multreg
      model = random
      nfullpredictors = 7
      ntestpredictors = 3
      partialcorr = 0.35
      ntotal = 100
      power = .;
run;

You can also express effects in terms of $R^2$ :

proc power;
   multreg
      model = fixed
      nfullpredictors = 7
      ntestpredictors = 3
      rsquarefull = 0.9
      rsquarediff = 0.1
      ntotal = .
      power = 0.9;
run;