The GLMSELECT Procedure
-
Overview

- Getting Started
-
Syntax

-
Details
 Model-Selection MethodsModel Selection IssuesCriteria Used in Model Selection MethodsCLASS Variable Parameterization and the SPLIT OptionMacro Variables Containing Selected ModelsUsing the STORE StatementBuilding the SSCP MatrixModel AveragingUsing Validation and Test DataCross ValidationExternal Cross ValidationDisplayed OutputODS Table NamesODS Graphics
Model-Selection MethodsModel Selection IssuesCriteria Used in Model Selection MethodsCLASS Variable Parameterization and the SPLIT OptionMacro Variables Containing Selected ModelsUsing the STORE StatementBuilding the SSCP MatrixModel AveragingUsing Validation and Test DataCross ValidationExternal Cross ValidationDisplayed OutputODS Table NamesODS Graphics -
Examples

- References
MODEL dependent = <effects> / <options> ;
The MODEL statement names the dependent variable and the explanatory effects, including covariates, main effects, constructed effects, interactions, and nested effects; for more information, see the section Specification of Effects in Chapter 44: The GLM Procedure. If you omit the explanatory effects, the procedure fits an intercept-only model.
After the keyword MODEL, the dependent (response) variable is specified, followed by an equal sign. The explanatory effects follow the equal sign.
Table 47.5 summarizes the options available in the MODEL statement.
Table 47.5: MODEL Statement Options
|
Option |
Description |
|---|---|
|
Requests details when cross validation is used |
|
|
Specifies how subsets for cross validation are formed |
|
|
Specifies details to be displayed |
|
|
Specifies the tolerance range for criterion comparisons |
|
|
Specifies the hierarchy of effects to impose |
|
|
Specifies models without an explicit intercept |
|
|
Requests that parameter estimates be displayed in the order in which the parameters first entered the model |
|
|
Specifies the model selection method |
|
|
Requests p-values in “ANOVA” and “Parameter Estimates” tables |
|
|
Specifies additional statistics to be displayed |
|
|
Adds standardized coefficients to “Parameter Estimates” tables |
You can specify the following options in the MODEL statement after a slash (/).
- CVDETAILS=ALL | COEFFS | CVPRESS
-
specifies the details that are produced when cross validation is requested as the CHOOSE=, SELECT=, or STOP= criterion in the MODEL statement. If n-fold cross validation is being used, then the training data are subdivided into n parts, and at each step of the selection process, models are obtained on each of the n subsets of the data obtained by omitting one of these parts. CVDETAILS=COEFFS requests that the parameter estimates obtained for each of these n subsets be included in the parameter estimates table. CVDETAILS=CVPRESS requests a table containing the predicted residual sum of squares of each of these models scored on the omitted subset. CVDETAILS=ALL requests both CVDETAILS=COEFFS and CVDETAILS=CVPRESS. If DETAILS=STEPS or DETAILS=ALL has been specified in the MODEL statement, then the requested CVDETAILS are produced for every step of the selection process.
- CVMETHOD=BLOCK<(n)> | RANDOM<(n)> | SPLIT<(n)> | INDEX (variable)
-
specifies how the training data are subdivided into n parts when you request n-fold cross validation by using any of the CHOOSE=CV, SELECT=CV, and STOP=CV suboptions of the SELECTION= option in the MODEL statement.
-
BLOCK requests that parts be formed of n blocks of consecutive training observations.
-
SPLIT requests that the ith part consist of training observations
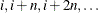 .
.
-
RANDOM assigns each training observation randomly to one of the n parts.
-
INDEX(variable) assigns observations to parts based on the formatted value of the named variable. This input data set variable is treated as a classification variable and the number of parts n is the number of distinct levels of this variable. By optionally naming this variable in a CLASS statement you can use the CLASS statement options ORDER= and MISSING to control how the levelization of this variable is done.
n defaults to 5 with CVMETHOD=BLOCK, CVMETHOD=SPLIT, or CVMETHOD=RANDOM. If you do not specify the CVMETHOD= option, then the CVMETHOD defaults to CVMETHOD=RANDOM(5).
-
- DETAILS=level | STEPS <(step options)>
-
specifies the level of detail produced, where level can be ALL, STEPS, or SUMMARY. The default if the DETAILS= option is omitted is DETAILS=SUMMARY. The DETAILS=ALL option produces the following:
-
entry and removal statistics for each variable selected in the model building process
-
ANOVA, fit statistics, and parameter estimates
-
entry and removal statistics for the top 10 candidates for inclusion or exclusion at each step
-
a selection summary table
The DETAILS=SUMMARY option produces only the selection summary table.
The option DETAILS=STEPS <(step options)> provides the step information and the selection summary table. The following options can be specified within parentheses after the DETAILS=STEPS option:
- ALL
-
requests ANOVA, fit statistics, parameter estimates, and entry or removal statistics for the top 10 candidates for inclusion or exclusion at each selection step.
- ANOVA
- FITSTATISTICS | FITSTATS | FIT
-
requests fit statistics at each selection step. The default set of statistics includes all the statistics named in the CHOOSE=, SELECT=, and STOP= suboptions specified in the MODEL statement SELECTION= option, but you can request additional statistics by specifying the STATS= option in the MODEL statement.
- PARAMETERESTIMATES | PARMEST
- CANDIDATES <(SHOW= ALL | n)>
-
requests entry or removal statistics for the best n candidate effects for inclusion or exclusion at each step. If you specify SHOW=ALL, then all candidates are shown. If SHOW= is not specified. then the best 10 candidates are shown. The entry or removal statistic is the statistic named in the SELECT= option that is specified in the SELECTION= option in the MODEL statement.
-
- FUZZ=value
-
specifies the tolerance range for criterion comparisons. Criterion values that differ by less than the tolerance are regarded as equal. If you specify FUZZ=0, then the comparisons are based on simple equality. The default is
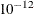 .
.
-
HIERARCHY=NONE | SINGLE | SINGLECLASS
HIER=NONE | SINGLE | SINGLECLASS -
specifies whether and how the model hierarchy requirement is applied. This option also controls whether a single effect or multiple effects are allowed to enter or leave the model in one step. You can specify that only classification effects, or both classification and continuous effects, be subject to the hierarchy requirement. The HIERARCHY= option is ignored unless you also specify one of the following options: SELECTION=FORWARD, SELECTION=BACKWARD, or SELECTION=STEPWISE.
Model hierarchy refers to the requirement that for any term to be in the model, all model effects contained in the term must be present in the model. For example, in order for the interaction A*B to enter the model, the main effects A and B must be in the model. Likewise, neither effect A nor effect B can leave the model while the interaction A*B is in the model.
You can specify the following values:
- NONE
-
specifies that model hierarchy not be maintained. Any single effect can enter or leave the model at any given step of the selection process.
- SINGLE
-
specifies that only one effect enter or leave the model at one time, subject to the model hierarchy requirement. For example, suppose that the model contains the main effects A and B and the interaction A*B. In the first step of the selection process, either A or B can enter the model. In the second step, the other main effect can enter the model. The interaction effect can enter the model only when both main effects have already entered. Also, before A or B can be removed from the model, the A*B interaction must first be removed. All effects (CLASS and interval) are subject to the hierarchy requirement.
- SINGLECLASS
-
is the same as HIERARCHY=SINGLE except that only CLASS effects are subject to the hierarchy requirement.
By default, HIERARCHY=NONE.
- NOINT
-
suppresses the intercept term that is otherwise included in the model.
- ORDERSELECT
-
specifies that for the selected model, effects be displayed in the order in which they first entered the model. If you do not specify the ORDERSELECT option, then effects in the selected model are displayed in the order in which they appeared in the MODEL statement.
- SELECTION=method <(method options)>
-
specifies the method used to select the model, optionally followed by parentheses enclosing options applicable to the specified method. The default if the SELECTION= option is omitted is SELECTION=STEPWISE.
You can specify the following methods, which are explained in detail in the section Model-Selection Methods:
- NONE
-
specifies no model selection.
- FORWARD
-
specifies forward selection. This method starts with no effects in the model and adds effects.
- BACKWARD
-
specifies backward elimination. This method starts with all effects in the model and deletes effects.
- STEPWISE
-
specifies stepwise regression. This is similar to the forward selection method except that effects already in the model do not necessarily stay there.
- LAR
-
specifies least angle regression. This method, like forward selection, starts with no effects in the model and adds effects. The parameter estimates at any step are “shrunk” when compared to the corresponding least squares estimates. If the model contains classification variables, then these classification variables are split. For more information, see the SPLIT option in the CLASS statement.
- LASSO
-
specifies the LASSO method, which adds and deletes parameters based on a version of ordinary least squares where the sum of the absolute regression coefficients is constrained. If the model contains classification variables, then these classification variables are split. For more information, see the SPLIT option in the CLASS statement.
- ELASTICNET
-
specifies the elastic net method, an extension of LASSO that estimates parameters based on a version of ordinary least squares in which both the sum of the absolute regression coefficients and the sum of the squared regression coefficients are constrained. If the model contains classification variables, then these classification variables are split. For more information, see the SPLIT option in the CLASS statement.
Table 47.6 lists the applicable suboptions for each of these methods.
Table 47.6: Applicable SELECTION= Options by Method
Option
FORWARD
BACKWARD
STEPWISE
LAR LASSO
ELASTICNET
STOP=
x
x
x
x
x
CHOOSE=
x
x
x
x
x
STEPS=
x
x
x
x
x
MAXSTEP=
x
x
x
x
x
SELECT=
x
x
x
INCLUDE=
x
x
x
SLENTRY=
x
x
SLSTAY=
x
x
DROP=
x
ADAPTIVE
x
LSCOEFFS
x
L1=
x
x
L1CHOICE=
x
x
L2=
x
L2STEPS=
x
L2LOW=
x
L2HIGH=
x
L2SEARCH=
x
ENSCALE
x
The syntax of the suboptions that you can specify in parentheses after the SELECTION= option method follows. Note that, as described in Table 47.6, not all selection suboptions are available for every SELECTION= method.
- ADAPTIVE <(<GAMMA=non-negative number> <INEST=SAS-data-set> )>
-
requests that adaptive weights be applied to each of the coefficients in the LAR and LASSO methods. You use the optional INEST= option to name the SAS data set that contains estimates that are used to form the adaptive weights for all the parameters in the model. If you do not specify an INEST= data set, then ordinary least squares estimates of the parameters in the model are used in forming the adaptive weights. You use the GAMMA= option to specify the power transformation that is applied to the parameters in forming the adaptive weights. By default, GAMMA=1.
- CHOOSE=criterion
-
specifies the criterion for choosing the model. The specified criterion is evaluated at each step of the selection process, and the model that yields the best value of the criterion is chosen. If the optimal value of the criterion occurs for models at more than one step, then the model that has the smallest number of parameters is chosen. If you do not specify the CHOOSE= option, then the model at the final step in the selection process is selected.
The criteria that you can specify in the CHOOSE= option are shown in Table 47.7. For more information about these criteria, see the section Criteria Used in Model Selection Methods.
Table 47.7: Criteria for the CHOOSE= Option
Criterion
Criterion
ADJRSQ
Adjusted R-square statistic
AIC
Akaike’s information criterion
AICC
Corrected Akaike’s information criterion
BIC
Sawa Bayesian information criterion
CP
Mallows’ C(p) statistic
CV
Predicted residual sum of square with k-fold cross validation
CVEX
Predicted residual sum of square with k-fold external cross validation
PRESS
Predicted residual sum of squares
SBC
Schwarz Bayesian information criterion
VALIDATE
Average square error for the validation data
For ADJRSQ, the chosen value is the largest one; for all other criteria, the smallest value is chosen. You can use the CHOOSE=VALIDATE option only if you have specified a VALDATA= data set in the PROC GLMSELECT statement or if you have reserved part of the input data for validation by using either a PARTITION statement or a
_ROLE_variable in the input data. The PRESS criterion is not available for SELECTION=ELASTICNET. - DROP=BEFOREADD | COMPETITIVE
-
specifies when effects are eligible to be dropped in the STEPWISE method. You can specify the following values:
- BEFOREADD
-
requests that currently in the model be examined to see if any meet the requirements to be removed from the model. If so, the effect that gives the best value of the removal criterion is dropped from the model and the stepwise method proceeds to the next step. Only when no effect currently in the model meets the requirement to be removed from the model are any effects added to the model.
- COMPETITIVE
-
requests that the SELECT= criterion be evaluated for all models in which an effect currently in the model is dropped or an effect not yet in the model is added. The effect whose removal or addition to the model yields the maximum improvement to the SELECT= criterion is dropped or added. You can specify DROP=COMPETITIVE only if the SELECT= criterion is not SL.
By default, DROP=BEFOREADD. If SELECT=SL, PROC GLMSELECT uses the traditional stepwise method as implemented in PROC REG.
- ENSCALE
-
requests that the solution to SELECTION=ELASTICNET be scaled to offset bias because of the double shrinkage inherent in the elastic net method (Zou and Hastie, 2005). This option applies only when SELECTION=ELASTICNET. The default is not to rescale the solution: this is the so-called naive elastic net.
- INCLUDE=n
-
forces the first n effects listed in the MODEL statement to be included in all models. The selection methods are performed on the other effects in the MODEL statement. The INCLUDE= option is available only when SELECTION=FORWARD, SELECTION=STEPWISE, and SELECTION=BACKWARD.
- L1=value
-
specifies the LASSO regularization or constraint parameter that is used when SELECTION=LASSO or SELECTION=ELASTICNET. This option is available only when you specify the STOP=L1 option with SELECTION=LASSO or SELECTION=ELASTICNET.
- L1CHOICE=NORM | RATIO | VALUE
-
specifies both the criterion used in the L1=value option and the criterion used in aggregating the results of
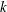 -fold external cross validation for computing the CVEXPRESS statistic. This option is available only when you specify SELECTION=LASSO
or SELECTION=ELASTICNET. You can specify the following values:
-fold external cross validation for computing the CVEXPRESS statistic. This option is available only when you specify SELECTION=LASSO
or SELECTION=ELASTICNET. You can specify the following values:
- NORM
-
indicates that the value specified in the L1=value option corresponds to the sum of the absolute values of the coefficients (the so-called L1 norm), and the
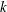 -fold external cross validation aggregation is based on the L1 norms.
-fold external cross validation aggregation is based on the L1 norms.
- RATIO
-
indicates that the value specified in the L1=value option corresponds to the ratio obtained by scaling the value of the LASSO regularization parameter to lie in the interval [0,1], and the
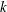 -fold external cross validation aggregation is based on the scaled ratios.
-fold external cross validation aggregation is based on the scaled ratios.
- VALUE
-
indicates that the value specified in the L1=value option corresponds to the actual value of the LASSO regularization parameter, and the
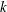 -fold external cross validation aggregation is based on the actual LASSO regularization parameters.
-fold external cross validation aggregation is based on the actual LASSO regularization parameters.
By default, L1CHOICE=RATIO.
- L2=value
-
specifies the ridge regularization parameter that is used when SELECTION=ELASTICNET. The L2= option is available only when SELECTION=ELASTICNET. If you specify the L2= option, then the value that you specify is used in defining the elastic net method, and the L2HIGH=, L2LOW=, L2SEARCH=, and L2STEPS= options are ignored. If you do not specify the L2 = option with SELECTION=ELASTICNET, then PROC GLMSELECT searches for the suitable value of L2 according to the L2HIGH=, L2LOW=, L2SEARCH=, and L2STEPS= options.
- L2HIGH=value
-
specifies the highest value used in the search of the ridge regression parameter L2 when SELECTION=ELASTICNET. If you specify the L2= option, then the L2HIGH= option is ignored. By default, L2HIGH=1.
- L2LOW=value
-
specifies the lowest value used in the search of the ridge regression parameter L2 when SELECTION=ELASTICNET. If you specify the L2= option, then the L2LOW= option is ignored. By default, L2LOW=0.
- L2SEARCH=GOLDEN | GRID
-
specifies the approach for the search of the ridge regression parameter L2 for the SELECTION=ELASTICNET option. You can specify the following values:
- GOLDEN
-
requests a golden section search of L2 in the range
![$[\hbox{low}, \hbox{high}]$](images/statug_glmselect0007.png) , where low and high are specified by the L2LOW= and L2HIGH= options, respectively.
, where low and high are specified by the L2LOW= and L2HIGH= options, respectively.
- GRID
-
requests a log scale grid search of L2 in the range
![$[\hbox{low}, \hbox{high}]$](images/statug_glmselect0007.png) , where low and high are specified by the L2LOW= and L2HIGH= options, respectively. If L2LOW=0, then the log scale grid search
for L2 is in the range
, where low and high are specified by the L2LOW= and L2HIGH= options, respectively. If L2LOW=0, then the log scale grid search
for L2 is in the range ![$[10^{-8}, \hbox{high}]$](images/statug_glmselect0008.png) plus 0.
plus 0.
If you specify the L2= option with SELECTION=ELASTICNET, then the L2SEARCH= option is ignored. By default, L2SEARCH=GRID.
- L2STEPS=n
-
specifies the number of steps in the search of the ridge regression parameter L2 when SELECTION=ELASTICNET. If you specify the L2 = option, then the L2STEPS= option is ignored. By default, L2STEPS=50.
- LSCOEFFS
-
requests a hybrid version of the LAR or LASSO method, in which the sequence of models is determined by the LAR or LASSO method but the coefficients of the parameters for the model at any step are determined by using ordinary least squares.
- MAXSTEP=n
-
specifies the maximum number of selection steps that are performed. The default value of n is the number of effects in the model statement for the forward, backward, and LAR methods and is two times the number of effects for the stepwise, LASSO, and elastic net methods.
- SELECT=criterion
-
specifies the criterion that PROC GLMSELECT uses to determine the order in which effects enter or leave at each step of the specified selection method. The SELECT= option is not valid with the LAR, LASSO, and elastic net methods. The criteria that you can specify with the SELECT= option are ADJRSQ, AIC, AICC, BIC, CP, CV, PRESS, RSQUARE, SBC, SL, and VALIDATE. For more information about these criteria, see the section Criteria Used in Model Selection Methods. The default value of the SELECT= criterion is SELECT=SBC. You can use SELECT=SL to request the traditional approach, in which effects enter and leave the model based on the significance level. For other SELECT= criteria, the effect that is selected to enter or leave at a step of the selection process is the effect whose addition to or removal from the current model gives the maximum improvement in the specified criterion.
-
SLENTRY=value
SLE=value -
specifies the significance level for entry, which is used when the STOP=SL or SELECT=SL option is specified. The defaults are 0.50 when SELECTION=FORWARD and 0.15 when SELECTION=STEPWISE.
-
SLSTAY=value
SLS=value -
specifies the significance level for staying in the model, which is used when the STOP=SL or SELECT=SL option is specified. The defaults are 0.10 when SELECTION=BACKWARD and 0.15 when SELECTION=STEPWISE.
- STEPS=n
-
specifies the number of selection steps to be done. If the STEPS= option is specified, the STOP= and MAXSTEP= options are ignored.
-
STOP=n
STOP=criterion -
specifies when PROC GLMSELECT is to stop the selection process. If the STEPS= option is specified, then the STOP= option is ignored. If the STOP=option does not cause the selection process to stop before the maximum number of steps for the selection method, then the selection process terminates at the maximum number of steps.
If you do not specify the STOP= option but do specify the SELECT= option, then the criterion named in the SELECT=option is also used as the STOP= criterion. If you do not specify either the STOP= or SELECT= option, then by default STOP=SBC.
If you specify STOP=n, then PROC GLMSELECT stops selection at the first step for which the selected model has n effects.
The nonnumeric arguments that you can specify in the STOP= option are shown in Table 47.8. For more information about these criteria, see the section Criteria Used in Model Selection Methods.
Table 47.8: Nonnumeric Criteria for the STOP= Option
Option
Criteria
NONE
ADJRSQ
Adjusted R-square statistic
AIC
Akaike’s information criterion
AICC
Corrected Akaike’s information criterion
BIC
Sawa Bayesian information criterion
CP
Mallows’ C(p) statistic
CV
Predicted residual sum of square with k-fold cross validation
L1
The LASSO regularization or constraint parameter
PRESS
Predicted residual sum of squares
SBC
Schwarz Bayesian information criterion
SL
Significance level
VALIDATE
Average square error for the validation data
When you use the SL criterion, selection stops at the step where the significance level for entry of all the effects not yet in the model is greater than the SLE= value for addition steps in the forward and stepwise methods and where the significance level for removal of any effect in the current model is smaller than the SLS= value in the backward and stepwise methods. When you use the ADJRSQ criterion, selection stops at the step where the next step would yield a model that has a smaller value of the adjusted R-square statistic; for all other criteria, selection stops at the step where the next step would yield a model that has a larger value of the criteria. You can use the VALIDATE option only if you have specified a VALDATA= data set in the PROC GLMSELECT statement or if you have reserved part of the input data for validation by using either a PARTITION statement or a
_ROLE_variable in the input data.The L1 criterion is available only when SELECTION=LASSO or SELECTION=ELASTICNET. When you use the L1 criterion, selection stops at the step where the LASSO regularization parameter is equal to the value specified by the L1=value option. The PRESS criterion is not available for SELECTION=ELASTICNET.
-
STAT|STATS=name
STATS=(names) -
specifies which model fit statistics are displayed in the fit summary table and fit statistics tables. If you omit the STATS= option, the default set of statistics that are displayed in these tables includes all the criteria specified in any of the CHOOSE=, SELECT=, and STOP= options specified in the MODEL statement SELECTION= option.
You can specify the following statistics:
- ADJRSQ
- AIC
- AICC
- ASE
-
specifies the average square errors for the training, test, and validation data. The ASE statistics for the test and validation data are reported only if you specify TESTDATA= or VALDATA= in the PROC GLMSELECT statement or if you have reserved part of the input data for testing or validation by using either a PARTITION statement or a
_ROLE_variable in the input data. - BIC
- CP
- FVALUE
-
specifies the F statistic for entering or departing effects.
- PRESS
- RSQUARE
- SBC
- SL
-
specifies the significance level of the F statistic for entering or departing effects.
The statistics ADJRSQ, AIC, AICC, FVALUE, RSQUARE, SBC, and SL can be computed with little computation cost. However, computing BIC, CP, CVPRESS, PRESS, and ASE for test and validation data when these are not used in any of the CHOOSE=, SELECT=, and STOP= options specified in the MODEL statement SELECTION= option can hurt performance.
-
SHOWPVALUES
SHOWPVALS -
displays p-values in the “ANOVA” and “Parameter Estimates” tables. These p-values are generally liberal because they are not adjusted for the fact that the terms in the model have been selected.
- STB
-
produces standardized regression coefficients. A standardized regression coefficient is computed by dividing a parameter estimate by the ratio of the sample standard deviation of the dependent variable to the sample standard deviation of the regressor.