-
BETAPRIORPARMS=pair-specification
BETAPRIORPARMS(pair-specification …pair-specification)
-
specifies the parameters for the normal prior distribution of the parameters that are associated with model effects (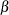 s). The pair-specification is of the form
s). The pair-specification is of the form 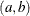 , and the values a and b are the mean and variance of the normal distribution, respectively. This option overrides the PRIOROPTIONS option.
, and the values a and b are the mean and variance of the normal distribution, respectively. This option overrides the PRIOROPTIONS option.
The form of the BETAPRIORPARMS with an equal sign and a single pair is used to specify one pair of prior parameters that applies
to all components in the mixture. In the following example, the two intercepts and the two regression coefficients all have
a 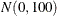 prior distribution:
prior distribution:
proc fmm;
model y = x / k=2;
bayes betapriorparms=(0,100);
run;
You can also provide a list of pairs to specify different sets of prior parameters for the various regression parameters and
components. For example:
proc fmm;
model y = x/ k=2;
bayes betapriorparms( (0,10) (0,20) (.,.) (3,100) );
run;
The simple linear regression in the first component has a 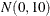 prior for the intercept and a
prior for the intercept and a 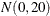 prior for the slope. The prior for the intercept in the second component uses the FMM default, whereas the prior for the
slope is
prior for the slope. The prior for the intercept in the second component uses the FMM default, whereas the prior for the
slope is 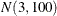 .
.
-
DIAGNOSTICS=ALL | NONE | (keyword-list)
DIAG=ALL | NONE | (keyword-list)
-
controls the computation of diagnostics for the posterior chain. You can request all posterior diagnostics by specifying DIAGNOSTICS=ALL
or suppress the computation of posterior diagnostics by specifying DIAGNOSTICS=NONE. The following keywords enable you to select subsets of posterior diagnostics; the default is DIAGNOSTICS=(AUTOCORR).
-
AUTOCORR <(LAGS= numeric-list)>
-
computes for each sampled parameter the autocorrelations of lags specified in the LAGS= list. Elements in the list are truncated
to integers, and repeated values are removed. If the LAGS= option is not specified, autocorrelations are computed by default
for lags 1, 5, 10, and 50. See the section Autocorrelations in Chapter 7: Introduction to Bayesian Analysis Procedures, for details.
-
ESS
-
computes an estimate of the effective sample size (Kass et al., 1998), the correlation time, and the efficiency of the chain for each parameter. See the section Effective Sample Size in Chapter 7: Introduction to Bayesian Analysis Procedures, for details.
-
GEWEKE <(geweke-options)>
-
computes the Geweke spectral density diagnostics (Geweke, 1992), which are essentially a two-sample t test between the first 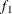 portion and the last
portion and the last 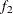 portion of the chain. The default is
portion of the chain. The default is 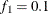 and
and 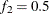 , but you can choose other fractions by using the following geweke-options:
, but you can choose other fractions by using the following geweke-options:
-
FRAC1=value
-
specifies the fraction 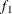 for the first window.
for the first window.
-
FRAC2=value
-
specifies the fraction 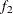 for the second window.
for the second window.
See the section Geweke Diagnostics in Chapter 7: Introduction to Bayesian Analysis Procedures, for details.
-
HEIDELBERGER <(Heidel-options)>
HEIDEL <(Heidel-options)>
-
computes the Heidelberger and Welch diagnostic (which consists of a stationarity test and a half-width test) for each variable.
The stationary diagnostic test tests the null hypothesis that the posterior samples are generated from a stationary process.
If the stationarity test is passed, a half-width test is then carried out. See the section Heidelberger and Welch Diagnostics in Chapter 7: Introduction to Bayesian Analysis Procedures, for more details.
These diagnostics are not performed by default. You can specify the DIAGNOSTICS=HEIDELBERGER option to request these diagnostics,
and you can also specify suboptions, such as DIAGNOSTICS=HEIDELBERGER(EPS=0.05), as follows:
-
MCERROR
MCSE
-
computes an estimate of the Monte Carlo standard error for each sampled parameter. See the section Standard Error of the Mean Estimate in Chapter 7: Introduction to Bayesian Analysis Procedures, for details.
-
MAXLAG=n
-
specifies the largest lag used in computing the effective sample size and the Monte Carlo standard error. Specifying this
option implies the ESS and MCERROR options. The default is MAXLAG=250.
-
RAFTERY <(Raftery-options)>
RL <(Raftery-options)>
-
computes the Raftery and Lewis diagnostics, which evaluate the accuracy of the estimated quantile (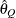 for a given Q
for a given Q 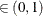 ) of a chain.
) of a chain. 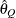 can achieve any degree of accuracy when the chain is allowed to run for a long time. The algorithm stops when the estimated
probability
can achieve any degree of accuracy when the chain is allowed to run for a long time. The algorithm stops when the estimated
probability 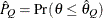 reaches within
reaches within 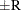 of the value Q with probability S; that is,
of the value Q with probability S; that is, 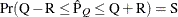 . See the section Raftery and Lewis Diagnostics in Chapter 7: Introduction to Bayesian Analysis Procedures, for more details. The Raftery-options enable you to specify Q, R, S, and a precision level
. See the section Raftery and Lewis Diagnostics in Chapter 7: Introduction to Bayesian Analysis Procedures, for more details. The Raftery-options enable you to specify Q, R, S, and a precision level  for a stationary test.
for a stationary test.
These diagnostics are not performed by default. You can specify the DIAGNOSTICS=RAFERTY option to request these diagnostics,
and you can also specify suboptions, such as DIAGNOSTICS=RAFERTY(QUANTILE=0.05), as follows:
-
QUANTILE=value
Q=value
-
specifies the order (a value between 0 and 1) of the quantile of interest. By default, QUANTILE=0.025.
-
ACCURACY=value
R=value
-
specifies a small positive number as the margin of error for measuring the accuracy of estimation of the quantile. By default,
ACCURACY=0.005.
-
PROB=value
S=value
-
specifies the probability of attaining the accuracy of the estimation of the quantile. By default, PROB=0.95.
-
EPS=value
-
specifies the tolerance level (a small positive number between 0 and 1) for the stationary test. By default, EPS=0.001.
-
MIXPRIORPARMS=K
MIXPRIORPARMS(value-list)
-
specifies the parameters used in constructing the Dirichlet prior distribution for the mixing parameters. If you specify MIXPRIORPARMS=K,
the parameters of the k-dimensional Dirichlet distribution are a vector that contains the number of components in the model (k), whatever that might be. You can specify an explicit list of parameters in value-list. If the MIXPRIORPARMS option is not specified, the default Dirichlet parameter vector is a vector of length k of ones. This results in a uniform prior over the unit simplex; for k=2, this is the uniform distribution. See the section Prior Distributions for the distribution function of the Dirichlet as used by the FMM procedure.
-
ESTIMATE=MEAN | MAP
-
determines which overall estimate is used, based on the posterior sample, in the computation of OUTPUT statistics and certain ODS graphics. By default, the arithmetic average of the (thinned) posterior sample is used. If you
specify ESTIMATE=MAP, the parameter vector is used that corresponds to the maximum log posterior density in the posterior
sample. In any event, a message is written to the SAS log if postprocessing results depend on a summary estimate of the posterior
sample.
-
INITIAL=DATA | MLE | MODE | RANDOM
-
determines how initial values for the Markov chain are obtained. The default when a conjugate sampler is used is INITIAL=DATA,
in which case the FMM procedure uses the same algorithm to obtain data-dependent starting values as it uses for maximum likelihood
estimation. If no conjugate sampler is available or if you use the METROPOLIS option to explicitly request that it not be
used, then the default is INITIAL=MLE, in which case the maximum likelihood estimates are used as the initial values. If the
maximum likelihood optimization fails, the FMM procedure switches to the default INITIAL=DATA.
The options INITIAL=MODE and INITIAL=RANDOM use the mode and random draws from the prior distribution, respectively, to obtain
initial values. If the mode does not exist or if it falls on the boundary of the parameter space, the prior mean is used instead.
-
METROPOLIS
-
requests that the FMM procedure use the Metropolis-Hastings sampling algorithm based on Gamerman (1997), even in situations where a conjugate sampler is available.
-
MUPRIORPARMS=pair-specification
MUPRIORPARMS(pair-specification …pair-specification)
-
specifies the parameters for the means in homogeneous mixtures without regression coefficients. The pair-specification is of the form 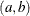 , where a and b are the two parameters of the prior distribution, optionally delimited with a comma. The actual distribution of the parameter
is implied by the distribution selected in the MODEL statement. For example, it is a normal distribution for a mixture of normals, a gamma distribution for a mixture of Poisson
variables, a beta distribution for a mixture of binary variables, and an inverse gamma distribution for a mixture of exponential
variables. This option overrides the PRIOROPTIONS option.
, where a and b are the two parameters of the prior distribution, optionally delimited with a comma. The actual distribution of the parameter
is implied by the distribution selected in the MODEL statement. For example, it is a normal distribution for a mixture of normals, a gamma distribution for a mixture of Poisson
variables, a beta distribution for a mixture of binary variables, and an inverse gamma distribution for a mixture of exponential
variables. This option overrides the PRIOROPTIONS option.
The parameters correspond as follows:
The two techniques for specifying the prior parameters with the MUPRIORPARMS option are as follows:
-
Specify an equal sign and a single pair of values:
proc fmm seed=12345;
model y = / k=2;
bayes mupriorparms=(0,50);
run;
-
Specify a list of parameter pairs within parentheses:
proc fmm seed=12345;
model y = / k=2;
bayes mupriorparms( (.,.) (1.4,10.5));
run;
If you specify an invalid value (outside of the parameter space for the prior distribution), the FMM procedure chooses the
default value and writes a message to the SAS log. If you want to use the default values for a particular parameter, you can
also specify missing values in the pair-specification. For example, the preceding list specification assigns default values for the first component and uses the values 1.4 and
10.5 for the mean and variance of the normal prior distribution in the second component. The first example assigns a 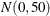 prior distribution to the means in both components.
prior distribution to the means in both components.
-
NBI=n
-
specifies the number of burn-in samples. During the burn-in phase, chains are not saved. The default is NBI=2000.
-
NMC=n
SAMPLE=n
-
specifies the number of Monte Carlo samples after the burn-in. Samples after the burn-in phase are saved unless they are thinned
with the THIN= option. The default is NMC=10000.
-
OUTPOST<(outpost-options)>=data-set
-
requests that the posterior sample be saved to a SAS data set. In addition to variables that contain log likelihood and log
posterior values, the OUTPOST data set contains variables for the parameters. The variable names for the parameters are generic
(Parm_1, Parm_2,  ,
, Parm_p). The labels of the parameters are descriptive and correspond to the “Parameter Mapping” table that is produced when the OUTPOST= option is in effect.
You can specify the following outpost-options in parentheses:
-
LOGPRIOR
-
adds the value of the log prior distribution to the data set.
-
NONSINGULAR | NONSING | COMPRESS
-
eliminates parameters that correspond to singular columns in the design matrix (and were not sampled) from the posterior data
set. This is the default.
-
SINGULAR | SING
-
adds columns of zeros to the data set in positions that correspond to singularities in the model or to parameters that were
not sampled for other reasons. By default, these columns of zeros are not written to the posterior data set.
-
PHIPRIORPARMS=pair-specification
PHIPRIORPARMS( pair-specification …pair-specification)
-
specifies the parameters for the inverse gamma prior distribution of the scale parameters (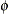 ’s) in the model. The pair-specification is of the form
’s) in the model. The pair-specification is of the form 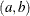 , and the values are chosen such that the prior distribution has mean
, and the values are chosen such that the prior distribution has mean 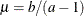 and variance
and variance 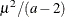 .
.
The form of the PHIPRIORPARMS with an equal sign and a single pair is used to specify one pair of prior parameters that applies
to all components in the mixture. For example:
proc fmm seed=12345;
model y = / k=2;
bayes phipriorparms=(2.001,1.001);
run;
The form with a list of pairs is used to specify different prior parameters for the scale parameters in different components.
For example:
proc fmm seed=12345;
model y = / k=2;
bayes phipriorparms( (.,1.001) (3.001,2.001) );
run;
If you specify an invalid value (outside of the parameter space for the prior distribution), the FMM procedure chooses the
default value and writes a message to the SAS log. If you want to use the default values for a particular parameter, you can
also specify missing values in the pair-specification. For example, the preceding list specification assigns default values for the first component a prior parameter and uses the value 1.001 for the b prior parameter. The second pair assigns 3.001 and 2.001 for the a and b prior parameters, respectively.
-
PRIOROPTIONS <=>(prior-options)
PRIOROPTS <=>(prior-options)
-
specifies options related to the construction of the prior distribution and the choice of their parameters. Some prior-options apply only in particular models. The BETAPRIORPARMS= and MUPRIORPARMS= options override this option.
You can specify the following prior-options:
-
CONDITIONAL | COND
-
chooses a conditional prior specification for the homogeneous normal and t distribution response components. The default prior specification in these models is an independence prior where the mean
of the hth component has prior 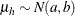 . The conditional prior is characterized by
. The conditional prior is characterized by 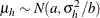 .
.
-
DEPENDENT | DEP
-
chooses a data-dependent prior for the homogeneous models without effects. The prior parameters a and b are chosen as follows, based on the distribution in the MODEL statement:
- Binary and binomial:
-
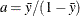 , b=1, and the prior distribution for the success probability is
, b=1, and the prior distribution for the success probability is 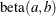 .
.
- Poisson:
-
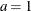 ,
, 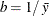 , and the prior distribution for
, and the prior distribution for 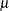 is
is 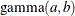 . See Frühwirth-Schnatter (2006, p. 280) and Viallefont, Richardson, and Greene (2002).
. See Frühwirth-Schnatter (2006, p. 280) and Viallefont, Richardson, and Greene (2002).
- Exponential:
-
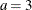 ,
, 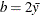 , and the prior distribution for
, and the prior distribution for 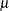 is inverse gamma with parameters a and b.
is inverse gamma with parameters a and b.
- Normal and t:
-
Under the default independence prior, the prior distribution for 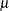 is
is 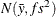 where f is the variance factor from the VAR= option and
where f is the variance factor from the VAR= option and
Under the default conditional prior specification, the prior for 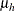 is
is 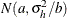 where
where 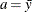 and
and 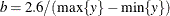 . The prior for the scale parameter is inverse gamma with parameters 1.28 and
. The prior for the scale parameter is inverse gamma with parameters 1.28 and 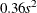 . For further details, see Raftery (1996) and Frühwirth-Schnatter (2006, p. 179).
. For further details, see Raftery (1996) and Frühwirth-Schnatter (2006, p. 179).
-
VAR=f
-
specifies the variance for normal prior distributions. The default is VAR=1000. This factor is used, for example, in determining
the prior variance of regression coefficients or in determining the prior variance of means in homogeneous mixtures of t or normal distributions (unless a data-dependent prior is used).
-
MLE<=r>
-
specifies that the prior distribution for regression variables be based on a multivariate normal distribution centered at
the MLEs and whose dispersion is a multiple r of the asymptotic MLE covariance matrix. The default is MLE=10. In other words, if you specify PRIOROPTIONS(MLE), the FMM
procedure chooses the prior distribution for the regression variables as ![$N(\widehat{\beta },10\mr {Var}[\widehat{\beta }])$](images/statug_fmm0106.png) where
where 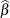 is the vector of maximum likelihood estimates. The prior for the scale parameter is inverse gamma with parameters 1.28 and
is the vector of maximum likelihood estimates. The prior for the scale parameter is inverse gamma with parameters 1.28 and
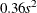 where
where
For further details, see Raftery (1996) and Frühwirth-Schnatter (2006, p. 179). If you specify PRIOROPTIONS(MLE) for the regression parameters, then the data-dependent prior is used for the scale
parameter; see the PRIOROPTIONS(DEPENDENT) option above.
The MLE option is not available for mixture models in which the parameters are estimated directly on the data scale, such
as homogeneous mixture models or mixtures of distributions without model effects for which a conjugate sampler is available.
By using the METROPOLIS option, you can always force the FMM procedure to abandon a conjugate sampler in favor of a Metropolis-Hastings sampling
algorithm to which the MLE option applies.
-
STATISTICS <(global-options)> = ALL | NONE | keyword | (keyword-list)
SUMMARIES <(global-options)> = ALL | NONE | keyword | (keyword-list)
-
controls the number of posterior statistics produced. Specifying STATISTICS=ALL is equivalent to specifying STATISTICS=(SUMMARY
INTERVAL). To suppress the computation of posterior statistics, specify STATISTICS=NONE. The default is STATISTICS=(SUMMARY
INTERVAL). See the section Summary Statistics in Chapter 7: Introduction to Bayesian Analysis Procedures, for more details.
The global-options include the following:
-
ALPHA=numeric-list
-
controls the coverage levels of the equal-tail credible intervals and the credible intervals of highest posterior density
(HPD) credible intervals. The ALPHA= values must be between 0 and 1. Each ALPHA= value produces a pair of 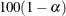 % equal-tail and HPD credible intervals for each sampled parameter. The default is ALPHA=0.05, which results in 95% credible
intervals for the parameters.
% equal-tail and HPD credible intervals for each sampled parameter. The default is ALPHA=0.05, which results in 95% credible
intervals for the parameters.
-
PERCENT=numeric-list
-
requests the percentile points of the posterior samples. The values in numeric-list must be between 0 and 100. The default is PERCENT=(25 50 75), which yields for each parameter the 25th, 50th, and 75th percentiles,
respectively.
The list of keywords includes the following:
-
SUMMARY
-
produces the means, standard deviations, and percentile points for the posterior samples. The default is to produce the 25th,
50th, and 75th percentiles; you can modify this list with the global PERCENT= option.
-
INTERVAL
-
produces equal-tail and HPD credible intervals. The default is to produce the 95% equal-tail credible intervals and 95% HPD
credible intervals, but you can use the ALPHA= global-option to request credible intervals for any probabilities.
-
THIN=n
THINNING=n
-
controls the thinning of the Markov chain after the burn-in. Only one in every k samples is used when THIN=k, and if NBI=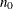 and NMC=n, the number of samples kept is
and NMC=n, the number of samples kept is
where [a] represents the integer part of the number a. The default is THIN=1—that is, all samples are kept after the burn-in phase.
-
TIMEINC=n
-
specifies a time interval in seconds to report progress during the burn-in and sampling phase. The time interval is approximate,
because the minimum time interval in which the FMM procedure can respond depends on the multithreading configuration.
