The CLUSTER Procedure
A dissimilarity measure ![]() is called an ultrametric if it satisfies the following conditions:
is called an ultrametric if it satisfies the following conditions:
-
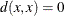 for all x
for all x
-
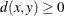 for all x, y
for all x, y
-
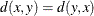 for all x, y
for all x, y
-
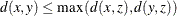 for all x, y, and z
for all x, y, and z
Any hierarchical clustering method induces a dissimilarity measure on the observations—say, ![]() . Let
. Let ![]() be the cluster with the fewest members that contains both
be the cluster with the fewest members that contains both ![]() and
and ![]() . Assume
. Assume ![]() was formed by joining
was formed by joining ![]() and
and ![]() . Then define
. Then define ![]() .
.
If the fusion of ![]() and
and ![]() reduces the number of clusters from g to
reduces the number of clusters from g to ![]() , then define
, then define ![]() . Johnson (1967) shows that if
. Johnson (1967) shows that if
then ![]() is an ultrametric. A method that always satisfies this condition is said to be a monotonic or ultrametric clustering method. All methods implemented in PROC CLUSTER except CENTROID, EML, and MEDIAN are ultrametric (Milligan, 1979; Batagelj, 1981).
is an ultrametric. A method that always satisfies this condition is said to be a monotonic or ultrametric clustering method. All methods implemented in PROC CLUSTER except CENTROID, EML, and MEDIAN are ultrametric (Milligan, 1979; Batagelj, 1981).
