The MULTTEST Procedure
An experiment was performed using Affymetrix® gene chips on the CD4 lymphocyte white blood cells of patients with and without a hereditary allergy (atopy) and possibly
with asthma. The Asthma-Atopy microarray data set and analysis are discussed in Gibson and Wolfinger (2004): a one-way ANOVA model of the log2mas5 variable (![]() summary statistics) is fit against a classification variable
summary statistics) is fit against a classification variable trt describing different asthma-atopy combinations in the patients, and the least squares means of the trt variable are computed.
For this example, a 1% random sample of least squares means having p-values exceeding 1E–6 is taken. The resulting data are recorded in the test data set, where the Probe_Set_ID variable identifies the probe and the Probt variable contains the p-values for the m = 121 tests, as follows:
data test; length Probe_Set_ID $9.; input Probe_Set_ID $ Probt @@; datalines; 200973_s_ .963316 201059_at .462754 201563_at .000409 201733_at .000819 201951_at .000252 202944_at .106550 203107_x_ .040396 203372_s_ .010911 203469_s_ .987234 203641_s_ .019296 203795_s_ .002276 204055_s_ .002328 205020_s_ .008628 205199_at .608129 205373_at .005209 205384_at .742381 205428_s_ .870533 205653_at .621671 205686_s_ .396440 205760_s_ .000002 206032_at .024661 206159_at .997627 206223_at .003702 206398_s_ .191682 206623_at .010030 206852_at .000004 207072_at .000214 207371_at .000013 207789_s_ .023623 207861_at .000002 207897_at .000007 208022_s_ .251999 208086_s_ .000361 208406_s_ .040182 208464_at .161468 209055_s_ .529824 209125_at .142276 209369_at .240079 209748_at .071750 209894_at .000042 209906_at .223282 210130_s_ .192187 210199_at .101623 210477_x_ .300038 210491_at .000078 210531_at .000784 210734_x_ .202931 210755_at .009644 210782_x_ .000011 211320_s_ .022896 211329_x_ .486869 211362_s_ .881798 211369_at .000030 211399_at .000008 211572_s_ .269788 211647_x_ .001301 213072_at .005019 213143_at .008711 213238_at .004824 213391_at .316133 213468_at .000172 213636_at .097133 213823_at .001678 213854_at .001921 213976_at .000299 214006_s_ .014616 214063_s_ .000361 214407_x_ .609880 214445_at .000009 214570_x_ .000002 214648_at .001255 214684_at .288156 214991_s_ .006695 215012_at .000499 215117_at .000136 215201_at .045235 215304_at .000816 215342_s_ .973786 215392_at .112937 215557_at .000007 215608_at .006204 215935_at .000027 215980_s_ .037382 216010_x_ .000354 216051_x_ .000003 216086_at .002310 216092_s_ .000056 216511_s_ .294776 216733_s_ .004823 216747_at .002902 216874_at .000117 216969_s_ .001614 217133_x_ .056851 217198_x_ .169196 217557_s_ .002966 217738_at .000005 218601_at .023817 218818_at .027554 219302_s_ .000039 219441_s_ .000172 219574_at .193737 219612_s_ .000075 219697_at .046476 219700_at .003049 219945_at .000066 219964_at .000684 220234_at .130064 220473_s_ .000017 220575_at .030223 220633_s_ .058460 220925_at .252465 221256_s_ .721731 221314_at .002307 221589_s_ .001810 221995_s_ .350859 222071_s_ .000062 222113_s_ .000023 222208_s_ .100961 222303_at .049265 37226_at .000749 60474_at .000423 run;
The following statements adjust the p-values in the test data set by using the adaptive adjustments (ADAPTIVEHOLM, ADAPTIVEHOCHBERG, ADAPTIVEFDR, and PFDR), which require an estimate of the number of true null hypotheses (![]() ) or proportion of true null hypotheses (
) or proportion of true null hypotheses (![]() ). This example illustrates some of the features and graphics for computing and evaluating these estimates. The NOPVALUE option is specified to suppress the display of the “p-Values” table.
). This example illustrates some of the features and graphics for computing and evaluating these estimates. The NOPVALUE option is specified to suppress the display of the “p-Values” table.
ods graphics on;
proc multtest inpvalues(Probt)=test plots=all seed=518498000
aholm ahoc afdr pfdr(positive) nopvalue;
id Probe_Set_ID;
run;
ods graphics off;
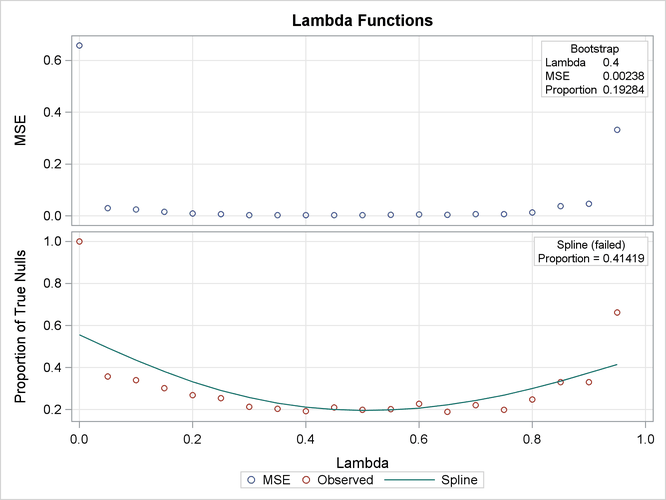
Output 61.6.1 lists the requested p-value adjustments, along with the selected value of the “Lambda” tuning parameter and the seed (specified with the SEED= option) used in the bootstrap method of estimating the number of true null hypotheses. The “Lambda Values” table lists the estimated number of true nulls for each value of ![]() , where you can see that the minimum MSE (0.002315) occurs at
, where you can see that the minimum MSE (0.002315) occurs at ![]() . Output 61.6.2 shows that the SPLINE method failed due to a large slope at
. Output 61.6.2 shows that the SPLINE method failed due to a large slope at ![]() , so the bootstrap method is used and the MSE plot is displayed.
, so the bootstrap method is used and the MSE plot is displayed.
Output 61.6.1: p and Lambda Values
| P-Value Adjustment Information | |
|---|---|
| P-Value Adjustment | Adaptive Holm |
| P-Value Adjustment | Adaptive Hochberg |
| P-Value Adjustment | Adaptive FDR |
| P-Value Adjustment | pFDR Q-Value |
| Lambda | 0.4 |
| Seed | 518498000 |
| Lambda Values | |||
|---|---|---|---|
| Lambda | MSE | NTrueNull Observed |
NTrueNull Spline |
| 0 | 0.657880 | 121.000000 | 67.318707 |
| 0.050000 | 0.030212 | 43.157895 | 59.812885 |
| 0.100000 | 0.024897 | 41.111111 | 52.636271 |
| 0.150000 | 0.014904 | 36.470588 | 46.033846 |
| 0.200000 | 0.008580 | 32.500000 | 40.172642 |
| 0.250000 | 0.006476 | 30.666667 | 35.157768 |
| 0.300000 | 0.002719 | 25.714286 | 31.046105 |
| 0.350000 | 0.002471 | 24.615385 | 27.861153 |
| 0.400000 | 0.002378 | 23.333333 | 25.595089 |
| 0.450000 | 0.003285 | 25.454545 | 24.217908 |
| 0.500000 | 0.003036 | 24.000000 | 23.687690 |
| 0.550000 | 0.003567 | 24.444444 | 23.965745 |
| 0.600000 | 0.005813 | 27.500000 | 25.016579 |
| 0.650000 | 0.004118 | 22.857143 | 26.809774 |
| 0.700000 | 0.006647 | 26.666667 | 29.321876 |
| 0.750000 | 0.006260 | 24.000000 | 32.512203 |
| 0.800000 | 0.013242 | 30.000000 | 36.315191 |
| 0.850000 | 0.037624 | 40.000000 | 40.618909 |
| 0.900000 | 0.046906 | 40.000000 | 45.274355 |
| 0.950000 | 0.332183 | 80.000000 | 50.117369 |
Output 61.6.3 also shows that the bootstrap estimate is used for the PFDR adjustment. The other adjustments have different default methods for estimating the number of true nulls.
Output 61.6.3: Adjustments and Their Default Estimation Method
| Estimated Number of True Null Hypotheses | |||
|---|---|---|---|
| P-Value Adjustment | Method | Estimate | Proportion |
| Adaptive Holm | Decreased Slope | 26 | 0.21488 |
| Adaptive Hochberg | Decreased Slope | 26 | 0.21488 |
| Adaptive FDR | Lowest Slope | 43 | 0.35537 |
| Positive FDR | Bootstrap | 23.3333 | 0.19284 |
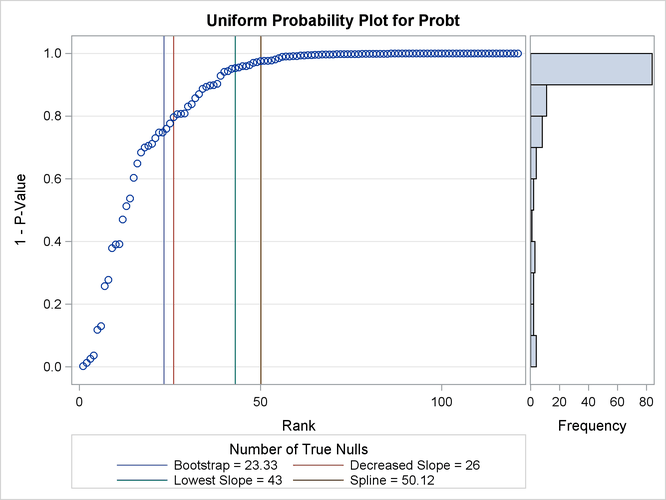
Output 61.6.4 displays the estimated number of true nulls ![]() against a uniform probability plot of the unadjusted p-values (if the p-values are distributed uniformly, the points on the plot will all lie on a straight line). According to Schweder and Spjøtvoll
(1982) and Hochberg and Benjamini (1990), the points on the left side of the plot should be approximately linear with slope
against a uniform probability plot of the unadjusted p-values (if the p-values are distributed uniformly, the points on the plot will all lie on a straight line). According to Schweder and Spjøtvoll
(1982) and Hochberg and Benjamini (1990), the points on the left side of the plot should be approximately linear with slope ![]() , so you can use this plot to evaluate whether your estimate of
, so you can use this plot to evaluate whether your estimate of ![]() seems reasonable.
seems reasonable.
The NTRUENULL= option provides several methods for estimating the number of true null hypotheses; the following table displays each method and its estimate for this example:
|
NTRUENULL= |
Estimate |
|---|---|
|
BOOTSTRAP |
23.3 |
|
DECREASESLOPE |
26 |
|
KSTEST |
35 |
|
LEASTSQUARES |
28 |
|
LOWESTSLOPE |
43 |
|
MEANDIFF |
42 |
|
SPLINE |
50.1 |
Another method of estimating the number of true null hypotheses fits a finite mixture model (mixing a uniform with a beta) to the distribution of the unadjusted p-values (Allison et al., 2002). Osborne (2006) provides the following PROC NLMIXED statements to fit this model:
proc nlmixed data=test;
parameters pi0=0.5 a=.1 b=.1;
pi1= 1-pi0;
bounds 0 <= pi0 <= 1;
loglikelihood= log(pi0+pi1*pdf('beta',Probt,a,b));
model Probt ~ general(loglikelihood);
run;
You might have to change the initial parameter values in the PARAMETERS statement to achieve convergence; see Chapter 64: The NLMIXED Procedure, for more information. This mixture model estimates ![]() , meaning that the distribution of p-values is completely specified by a single beta distribution. If the estimate were, say,
, meaning that the distribution of p-values is completely specified by a single beta distribution. If the estimate were, say, ![]() , you could then specify it as follows:
, you could then specify it as follows:
proc multtest inpvalues(Probt)=test ptruenull=0.10
aholm ahoc afdr pfdr(positive) nopvalue;
id Probe_Set_ID;
run;
A plot of the unadjusted and adjusted p-values for each test is also produced. Due to the large number of tests and adjustments, the plot is not very informative and is not displayed here.
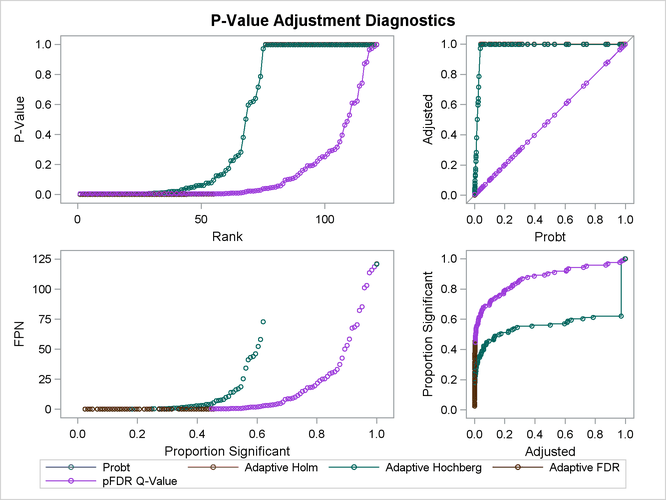
The top two plots in Output 61.6.5 show how the adjusted values compare with each other and the unadjusted p-values. The PFDR and AFDR adjustments are eventually smaller than the unadjusted p-values since they control the false discovery rate. The adaptive Holm and Hochberg adjustments are almost identical, so the adaptive Holm values are mostly obscured in all four plots. The plot of the Proportion Significant versus the Adjusted p-values tells you how many of the tests are significant for each cutoff, while the plot of the number of false positives (FPN) versus the Proportion Significant tells you how many false positives you can expect for that cutoff.
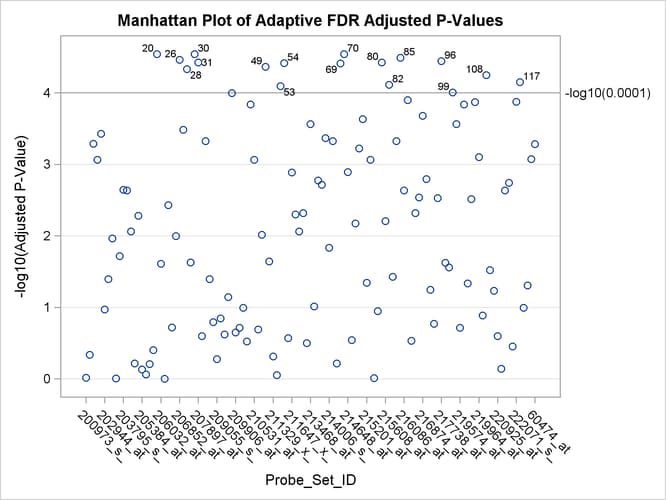
A Manhattan plot displays –log![]() of the adjusted p-values, so the most significant tests stand out at the top of the plot. The default plot is not displayed here. The following
statements create a Manhattan plot of the adaptive FDR p-values, with the most significant tests labeled with their observation number. The ID values are displayed on the X axis,
and the VREF= option specifies the significance level. This plot is typically created with many more p-values, and special ODS Graphics options such as the LABELMAX= option might be required to display the graph. If memory usage
is an issue, you might want to store your p-values and use the SGPLOT procedure to create a similar graph.
of the adjusted p-values, so the most significant tests stand out at the top of the plot. The default plot is not displayed here. The following
statements create a Manhattan plot of the adaptive FDR p-values, with the most significant tests labeled with their observation number. The ID values are displayed on the X axis,
and the VREF= option specifies the significance level. This plot is typically created with many more p-values, and special ODS Graphics options such as the LABELMAX= option might be required to display the graph. If memory usage
is an issue, you might want to store your p-values and use the SGPLOT procedure to create a similar graph.
ods graphics on / labelmax=1000; proc multtest inpvalues(Probt)=test afdr nopvalue plots=Manhattan(label=obs vref=0.0001); id Probe_Set_ID; run; ods graphics off;
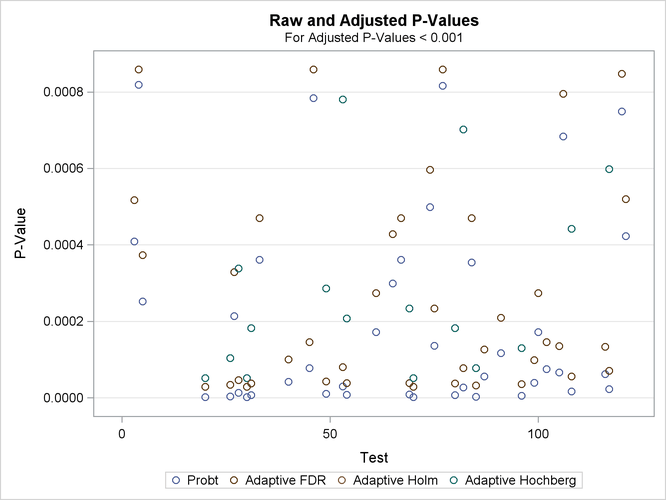
If you have a lot of tests, the “Raw and Adjusted p-Values” and “P-Value Adjustment Diagnostics” plots can be more informative if you suppress some of the tests. In the following statements, the SIGONLY=0.001 option selects tests with adjusted p-values < 0.001 for display. Output 61.6.7 displays tests with their “significant” adjusted p-values:
ods graphics on;
proc multtest inpvalues(Probt)=test plots(sigonly=0.001)=PByTest
aholm ahoc afdr pfdr(positive) nopvalue;
run;
ods graphics off;