The GLIMMIX Procedure

Automatic Variables

To specify your own link or variance function you can use SAS programming statements and draw on the following automatic variables:

_LINP_

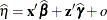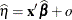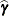is the current value of the linear predictor. It equals either $\widehat{\eta } = \mb {x}’\widehat{\bbeta } + \mb {z}’\widehat{\bgamma } + o$ or $\widehat{\eta } = \mb {x}’\widehat{\bbeta } + o$ , where o is the value of the offset variable, or 0 if no offset is specified. 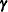The estimated random effects solutions $\widehat{\bgamma }$ are used in the calculation of the linear predictor during the model fitting phase, if a linearization expands about the current values of $\bgamma$ . During the computation of output statistics, the EBLUPs are used if statistics depend on them. For example, the following statements add the variable p to the output data set glimmixout:

proc glimmix;
   model y = x / dist=binary;
   random int / subject=b;
   p = 1/(1+exp(-_linp_);
   output out=glimmixout;
   id p;
run;

Because no output statistics are requested in the OUTPUT statement that depend on the random-effects solutions (BLUPs, EBEs), the value of _LINP_ in this example equals 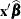$\mb {x}’\widehat{\bbeta }$ . On the contrary, the following statements also request conditional residuals on the logistic scale:

proc glimmix;
   model y = x / dist=binary;
   random int / subject=b;
   p = 1/(1+exp(-_linp_);
   output out=glimmixout resid(blup)=r;
   id p;
run;

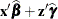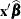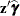The value of _LINP_ when computing the variable p is $\mb {x}’\widehat{\bbeta } + \mb {z}’\widehat{\bgamma }$ . To ensure that computed statistics are formed from $\mb {x}’\widehat{\bbeta }$ and $\mb {z}’\widehat{\bgamma }$ terms as needed, it is recommended that you use the automatic variables _XBETA_ and _ZGAMMA_ instead of _LINP_.

_MU_

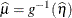expresses the mean of an observation as a function of the linear predictor, $\widehat{\mu } = g^{-1}(\widehat{\eta })$ .

_N_

is the observation number in the sequence of the data read.

_VARIANCE_

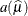is the estimate of the variance function, $a(\widehat{\mu })$ .

_XBETA_

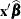equals $\mb {x}’\widehat{\bbeta }$ .

_ZGAMMA_

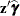equals $\mb {z}’\widehat{\bgamma }$ .

The automatic variable _N_ is incremented whenever the procedure reads an observation from the data set. Observations that are not used in the analysis—for example, because of missing values or invalid weights—are counted. The counter is reset to 1 at the start of every new BY group. Only in some circumstances will _N_ equal the actual observation number. The symbol should thus be used sparingly to avoid unexpected results.

You must observe the following syntax rules when you use the automatic variables. The _LINP_ symbol cannot appear on the left side of programming statements; you cannot make an assignment to the _LINP_ variable. The value of the linear predictor is controlled by the CLASS, MODEL, and RANDOM statements as well as the current parameter estimates and solutions. You can, however, use the _LINP_ variable on the right side of other operations. Suppose, for example, that you want to transform the linear predictor prior to applying the inverse log link. The following statements are not valid because the linear predictor appears in an assignment:

proc glimmix;
   _linp_ = sqrt(abs(_linp_));
   _mu_   = exp(_linp_);
   model count = logtstd / dist=poisson;
run;

The next statements achieve the desired result:

proc glimmix;
   _mu_ = exp(sqrt(abs(_linp_)));
   model count = logtstd / dist=poisson;
run;

If the value of the linear predictor is altered in any way through programming statements, you need to ensure that an assignment to _MU_ follows. The assignment to variable P in the next set of GLIMMIX statements is without effect:

proc glimmix;
   p = _linp_ + rannor(454);
   model count = logtstd / dist=poisson;
run;

A user-defined link function is implied by expressing _MU_ as a function of _LINP_. That is, if $\mu = g^{-1}(\eta )$ , you are providing an expression for the inverse link function with programming statements. It is neither necessary nor possible to give an expression for the inverse operation, $\eta = g(\mu )$ . The variance function is determined by expressing _VARIANCE_ as a function of _MU_. If the _MU_ variable appears in an assignment statement inside PROC GLIMMIX, the LINK= option of the MODEL statement is ignored. If the _VARIANCE_ function appears in an assignment statement, the DIST= option is ignored. Furthermore, the associated variance function per Table 41.20 is not honored. In short, user-defined expressions take precedence over built-in defaults.

If you specify your own link and variance function, the assignment to _MU_ must precede an assignment to the variable _VARIANCE_.

The following two sets of GLIMMIX statements yield the same parameter estimates, but the models differ statistically:

proc glimmix;
   class block entry;
   model y/n = block entry / dist=binomial link=logit;
run;

proc glimmix;
   class block entry;
   prob = 1 / (1+exp(- _linp_));
   _mu_ = n * prob ;
   _variance_ = n * prob *(1-prob);
   model y = block entry;
run;

The first GLIMMIX invocation models the proportion as a binomial proportion with a logit link. The DIST= and LINK= options are superfluous in this case, because the GLIMMIX procedure defaults to the binomial distribution in light of the events/trials syntax. The logit link is that distribution’s default link. The second set of GLIMMIX statements models the count variable y and takes the binomial sample size into account through assignments to the mean and variance function. In contrast to the first set of GLIMMIX statements, the distribution of y is unknown. Only its mean and variance are known. The model parameters are estimated by maximum likelihood in the first case and by quasi-likelihood in the second case.