The GLIMMIX Procedure
-
Overview

-
Getting Started

-
Syntax
 PROC GLIMMIX StatementBY StatementCLASS StatementCODE StatementCONTRAST StatementCOVTEST StatementEFFECT StatementESTIMATE StatementFREQ StatementID StatementLSMEANS StatementLSMESTIMATE StatementMODEL StatementNLOPTIONS StatementOUTPUT StatementPARMS StatementRANDOM StatementSLICE StatementSTORE StatementWEIGHT StatementProgramming StatementsUser-Defined Link or Variance Function
PROC GLIMMIX StatementBY StatementCLASS StatementCODE StatementCONTRAST StatementCOVTEST StatementEFFECT StatementESTIMATE StatementFREQ StatementID StatementLSMEANS StatementLSMESTIMATE StatementMODEL StatementNLOPTIONS StatementOUTPUT StatementPARMS StatementRANDOM StatementSLICE StatementSTORE StatementWEIGHT StatementProgramming StatementsUser-Defined Link or Variance Function -
Details
 Generalized Linear Models TheoryGeneralized Linear Mixed Models TheoryGLM Mode or GLMM ModeStatistical Inference for Covariance ParametersDegrees of Freedom MethodsEmpirical Covariance (Sandwich) EstimatorsExploring and Comparing Covariance MatricesProcessing by SubjectsRadial Smoothing Based on Mixed ModelsOdds and Odds Ratio EstimationParameterization of Generalized Linear Mixed ModelsResponse-Level Ordering and ReferencingComparing the GLIMMIX and MIXED ProceduresSingly or Doubly Iterative FittingDefault Estimation TechniquesDefault OutputNotes on Output StatisticsODS Table NamesODS Graphics
Generalized Linear Models TheoryGeneralized Linear Mixed Models TheoryGLM Mode or GLMM ModeStatistical Inference for Covariance ParametersDegrees of Freedom MethodsEmpirical Covariance (Sandwich) EstimatorsExploring and Comparing Covariance MatricesProcessing by SubjectsRadial Smoothing Based on Mixed ModelsOdds and Odds Ratio EstimationParameterization of Generalized Linear Mixed ModelsResponse-Level Ordering and ReferencingComparing the GLIMMIX and MIXED ProceduresSingly or Doubly Iterative FittingDefault Estimation TechniquesDefault OutputNotes on Output StatisticsODS Table NamesODS Graphics -
Examples
 Binomial Counts in Randomized BlocksMating Experiment with Crossed Random EffectsSmoothing Disease Rates; Standardized Mortality RatiosQuasi-likelihood Estimation for Proportions with Unknown DistributionJoint Modeling of Binary and Count DataRadial Smoothing of Repeated Measures DataIsotonic Contrasts for Ordered AlternativesAdjusted Covariance Matrices of Fixed EffectsTesting Equality of Covariance and Correlation MatricesMultiple Trends Correspond to Multiple Extrema in Profile LikelihoodsMaximum Likelihood in Proportional Odds Model with Random EffectsFitting a Marginal (GEE-Type) ModelResponse Surface Comparisons with Multiplicity AdjustmentsGeneralized Poisson Mixed Model for Overdispersed Count DataComparing Multiple B-SplinesDiallel Experiment with Multimember Random EffectsLinear Inference Based on Summary Data
Binomial Counts in Randomized BlocksMating Experiment with Crossed Random EffectsSmoothing Disease Rates; Standardized Mortality RatiosQuasi-likelihood Estimation for Proportions with Unknown DistributionJoint Modeling of Binary and Count DataRadial Smoothing of Repeated Measures DataIsotonic Contrasts for Ordered AlternativesAdjusted Covariance Matrices of Fixed EffectsTesting Equality of Covariance and Correlation MatricesMultiple Trends Correspond to Multiple Extrema in Profile LikelihoodsMaximum Likelihood in Proportional Odds Model with Random EffectsFitting a Marginal (GEE-Type) ModelResponse Surface Comparisons with Multiplicity AdjustmentsGeneralized Poisson Mixed Model for Overdispersed Count DataComparing Multiple B-SplinesDiallel Experiment with Multimember Random EffectsLinear Inference Based on Summary Data - References
This example of a repeated measures study is taken from Diggle, Liang, and Zeger (1994, p. 100). The data consist of body weights of 27 cows, measured at 23 unequally spaced time points over a period of approximately
22 months. Following Diggle, Liang, and Zeger (1994), one animal is removed from the analysis, one observation is removed according to their Figure 5.7, and the time is shifted
to start at 0 and is measured in 10-day increments. The design is a ![]() factorial, and the factors are the infection of an animal with M. paratuberculosis and whether the animal is receiving iron dosing.
factorial, and the factors are the infection of an animal with M. paratuberculosis and whether the animal is receiving iron dosing.
The following DATA steps create the data and arrange them in univariate format.
data times;
input time1-time23;
datalines;
122 150 166 179 219 247 276 296 324 354 380 445
478 508 536 569 599 627 655 668 723 751 781
;
data cows;
if _n_ = 1 then merge times;
array t{23} time1 - time23;
array w{23} weight1 - weight23;
input cow iron infection weight1-weight23 @@;
do i=1 to 23;
weight = w{i};
tpoint = (t{i}-t{1})/10;
output;
end;
keep cow iron infection tpoint weight;
datalines;
1 0 0 4.7 4.905 5.011 5.075 5.136 5.165 5.298 5.323
5.416 5.438 5.541 5.652 5.687 5.737 5.814 5.799
5.784 5.844 5.886 5.914 5.979 5.927 5.94
2 0 0 4.868 5.075 5.193 5.22 5.298 5.416 5.481 5.521
5.617 5.635 5.687 5.768 5.799 5.872 5.886 5.872
5.914 5.966 5.991 6.016 6.087 6.098 6.153
3 0 0 4.868 5.011 5.136 5.193 5.273 5.323 5.416 5.46
5.521 5.58 5.617 5.687 5.72 5.753 5.784 5.784
5.784 5.814 5.829 5.872 5.927 5.9 5.991
4 0 0 4.828 5.011 5.136 5.193 5.273 5.347 5.438 5.561
5.541 5.598 5.67 . 5.737 5.844 5.858 5.872
5.886 5.927 5.94 5.979 6.052 6.028 6.12
5 1 0 4.787 4.977 5.043 5.136 5.106 5.298 5.298 5.371
5.438 5.501 5.561 5.652 5.67 5.737 5.784 5.768
5.784 5.784 5.829 5.858 5.914 5.9 5.94
6 1 0 4.745 4.868 5.043 5.106 5.22 5.298 5.347 5.347
5.416 5.501 5.561 5.58 5.687 5.72 5.737 5.72
5.737 5.753 5.768 5.784 5.844 5.844 5.9
7 1 0 4.745 4.905 5.011 5.106 5.165 5.273 5.371 5.416
5.416 5.521 5.541 5.635 5.687 5.704 5.784 5.768
5.768 5.814 5.829 5.858 5.94 5.94 6.004
8 0 1 4.942 5.106 5.136 5.193 5.298 5.347 5.46 5.521
5.561 5.58 5.635 5.704 5.784 5.823 5.858 5.9
5.94 5.991 6.016 6.064 6.052 6.016 5.979
9 0 1 4.605 4.745 4.868 4.905 4.977 5.22 5.165 5.22
5.22 5.247 5.298 5.416 5.501 5.521 5.58 5.58
5.635 5.67 5.72 5.753 5.799 5.829 5.858
10 0 1 4.7 4.868 4.905 4.977 5.011 5.106 5.165 5.22
5.22 5.22 5.273 5.384 5.438 5.438 5.501 5.501
5.541 5.598 5.58 5.635 5.687 5.72 5.704
11 0 1 4.828 5.011 5.075 5.165 5.247 5.323 5.394 5.46
5.46 5.501 5.541 5.609 5.687 5.704 5.72 5.704
5.704 5.72 5.737 5.768 5.858 5.9 5.94
12 0 1 4.7 4.828 4.905 5.011 5.075 5.165 5.247 5.298
5.298 5.323 5.416 5.505 5.561 5.58 5.561 5.635
5.687 5.72 5.72 5.737 5.784 5.814 5.799
13 0 1 4.828 5.011 5.075 5.136 5.22 5.273 5.347 5.416
5.438 5.416 5.521 5.628 5.67 5.687 5.72 5.72
5.799 5.858 5.872 5.914 5.94 5.991 6.016
14 0 1 4.828 4.942 5.011 5.075 5.075 5.22 5.273 5.298
5.323 5.298 5.394 5.489 5.541 5.58 5.617 5.67
5.704 5.753 5.768 5.814 5.872 5.927 5.927
15 0 1 4.745 4.905 4.977 5.075 5.193 5.22 5.298 5.323
5.394 5.394 5.438 5.583 5.617 5.652 5.687 5.72
5.753 5.768 5.814 5.844 5.886 5.886 5.886
16 0 1 4.7 4.868 5.011 5.043 5.106 5.165 5.247 5.298
5.347 5.371 5.438 5.455 5.617 5.635 5.704 5.737
5.784 5.768 5.814 5.844 5.886 5.94 5.927
17 1 1 4.605 4.787 4.828 4.942 5.011 5.136 5.22 5.247
5.273 5.247 5.347 5.366 5.416 5.46 5.541 5.481
5.501 5.635 5.652 5.598 5.635 5.635 5.598
18 1 1 4.828 4.977 5.011 5.136 5.273 5.298 5.371 5.46
5.416 5.416 5.438 5.557 5.617 5.67 5.72 5.72
5.799 5.858 5.886 5.914 5.979 6.004 6.028
19 1 1 4.7 4.905 4.942 5.011 5.043 5.136 5.193 5.193
5.247 5.22 5.323 5.338 5.371 5.394 5.438 5.416
5.501 5.561 5.541 5.58 5.652 5.67 5.704
20 1 1 4.745 4.905 4.977 5.043 5.136 5.273 5.347 5.394
5.416 5.394 5.521 5.617 5.617 5.617 5.67 5.635
5.652 5.687 5.652 5.617 5.687 5.768 5.814
21 1 1 4.787 4.942 4.977 5.106 5.165 5.247 5.323 5.416
5.394 5.371 5.438 5.521 5.521 5.561 5.635 5.617
5.687 5.72 5.737 5.737 5.768 5.768 5.704
22 1 1 4.605 4.828 4.828 4.977 5.043 5.165 5.22 5.273
5.247 5.22 5.298 5.375 5.371 5.416 5.501 5.501
5.521 5.561 5.617 5.635 5.72 5.737 5.768
23 1 1 4.7 4.905 5.011 5.075 5.106 5.22 5.22 5.298
5.323 5.347 5.416 5.472 5.501 5.541 5.598 5.598
5.598 5.652 5.67 5.704 5.737 5.768 5.784
24 1 1 4.745 4.942 5.011 5.075 5.106 5.247 5.273 5.323
5.347 5.371 5.416 5.481 5.501 5.541 5.598 5.598
5.635 5.687 5.704 5.72 5.829 5.844 5.9
25 1 1 4.654 4.828 4.828 4.977 4.977 5.043 5.136 5.165
5.165 5.165 5.193 5.204 5.22 5.273 5.371 5.347
5.46 5.58 5.635 5.67 5.753 5.799 5.844
26 1 1 4.828 4.977 5.011 5.106 5.165 5.22 5.273 5.323
5.371 5.394 5.46 5.576 5.652 5.617 5.687 5.67
5.72 5.784 5.784 5.784 5.829 5.814 5.844
;
The mean response profiles of the cows are not of particular interest; what matters are inferences about the Iron effect, the Infection effect, and their interaction. Nevertheless, the body weight of the cows changes over the 22-month period, and you need to
account for these changes in the analysis. A reasonable approach is to apply the approximate low-rank smoother to capture
the trends over time. This approach frees you from having to stipulate a parametric model for the response trajectories over
time. In addition, you can test hypotheses about the smoothing parameter; for example, whether it should be varied by treatment.
The following statements fit a model with a ![]() factorial treatment structure and smooth trends over time, choosing the Newton-Raphson algorithm with ridging for the optimization:
factorial treatment structure and smooth trends over time, choosing the Newton-Raphson algorithm with ridging for the optimization:
proc glimmix data=cows;
t2 = tpoint / 100;
class cow iron infection;
model weight = iron infection iron*infection tpoint;
random t2 / type=rsmooth subject=cow
knotmethod=kdtree(bucket=100 knotinfo);
output out=gmxout pred(blup)=pred;
nloptions tech=newrap;
run;
The continuous time effect appears in both the MODEL statement (tpoint) and the RANDOM statement (t2). Because the variance of the radial smoothing component depends on the temporal metric, the time scale was rescaled for
the RANDOM effect to move the parameter estimate away from the boundary. The knots of the radial smoother are selected as the vertices
of a k-d tree. Specifying BUCKET=100 sets the bucket size of the tree to b = 100. Because measurements at each time point are available for 26 (or 25) cows, this groups approximately four time points
in a single bucket. The KNOTINFO keyword of the KNOTMETHOD= option requests a printout of the knot locations for the radial smoother. The OUTPUT statement saves the predictions of the mean of each observations to the data set gmxout. Finally, the TECH=NEWRAP option in the NLOPTIONS statement specifies the Newton-Raphson algorithm for the optimization technique.
The “Class Level Information” table lists the number of levels of the Cow, Iron, and Infection effects (Output 41.6.1).
Output 41.6.1: Model Information and Class Levels in Repeated Measures Analysis
| Model Information | |
|---|---|
| Data Set | WORK.COWS |
| Response Variable | weight |
| Response Distribution | Gaussian |
| Link Function | Identity |
| Variance Function | Default |
| Variance Matrix Blocked By | cow |
| Estimation Technique | Restricted Maximum Likelihood |
| Degrees of Freedom Method | Containment |
| Class Level Information | ||
|---|---|---|
| Class | Levels | Values |
| cow | 26 | 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 |
| iron | 2 | 0 1 |
| infection | 2 | 0 1 |
The “Radial Smoother Knots for RSmooth(t2)” table displays the knots computed from the vertices of the t2 k-d tree (Output 41.6.2). Notice that knots are spaced unequally and that the extreme time points are among the knot locations. The “Number of Observations” table shows that one observation was not used in the analysis. The 12th observation for cow 4 has a missing value.
Output 41.6.2: Knot Information and Number of Observations
| Radial Smoother Knots for RSmooth(t2) |
|
|---|---|
| Knot Number | t2 |
| 1 | 0 |
| 2 | 0.04400 |
| 3 | 0.1250 |
| 4 | 0.2020 |
| 5 | 0.3230 |
| 6 | 0.4140 |
| 7 | 0.5050 |
| 8 | 0.6010 |
| 9 | 0.6590 |
| Number of Observations Read | 598 |
|---|---|
| Number of Observations Used | 597 |
The “Dimensions” table shows that the model contains only two covariance parameters, the G-side variance of the spline coefficients (![]() ) and the R-side scale parameter (
) and the R-side scale parameter (![]() , Output 41.6.3). For each subject (cow), there are nine columns in the
, Output 41.6.3). For each subject (cow), there are nine columns in the ![]() matrix, one per knot location. The GLIMMIX procedure processes these data by subjects (cows).
matrix, one per knot location. The GLIMMIX procedure processes these data by subjects (cows).
Output 41.6.3: Dimensions Information in Repeated Measures Analysis
| Dimensions | |
|---|---|
| G-side Cov. Parameters | 1 |
| R-side Cov. Parameters | 1 |
| Columns in X | 10 |
| Columns in Z per Subject | 9 |
| Subjects (Blocks in V) | 26 |
| Max Obs per Subject | 23 |
The “Optimization Information” table displays information about the optimization process. Because fixed effects and the residual scale parameter can be profiled from the optimization, the iterative algorithm involves only a single covariance parameter, the variance of the spline coefficients (Output 41.6.4).
Output 41.6.4: Optimization Information in Repeated Measures Analysis
| Optimization Information | |
|---|---|
| Optimization Technique | Newton-Raphson |
| Parameters in Optimization | 1 |
| Lower Boundaries | 1 |
| Upper Boundaries | 0 |
| Fixed Effects | Profiled |
| Residual Variance | Profiled |
| Starting From | Data |
After 11 iterations, the optimization process terminates (Output 41.6.5). In this case, the absolute gradient convergence criterion was met.
Output 41.6.5: Iteration History and Convergence Status
| Iteration History | |||||
|---|---|---|---|---|---|
| Iteration | Restarts | Evaluations | Objective Function |
Change | Max Gradient |
| 0 | 0 | 4 | -1302.549272 | . | 20.33682 |
| 1 | 0 | 3 | -1451.587367 | 149.03809501 | 9.940495 |
| 2 | 0 | 3 | -1585.640946 | 134.05357887 | 4.71531 |
| 3 | 0 | 3 | -1694.516203 | 108.87525722 | 2.176741 |
| 4 | 0 | 3 | -1775.290458 | 80.77425512 | 0.978577 |
| 5 | 0 | 3 | -1829.966584 | 54.67612585 | 0.425724 |
| 6 | 0 | 3 | -1862.878184 | 32.91160012 | 0.175992 |
| 7 | 0 | 3 | -1879.329133 | 16.45094875 | 0.066061 |
| 8 | 0 | 3 | -1885.175082 | 5.84594887 | 0.020137 |
| 9 | 0 | 3 | -1886.238032 | 1.06295071 | 0.00372 |
| 10 | 0 | 3 | -1886.288519 | 0.05048659 | 0.000198 |
| 11 | 0 | 3 | -1886.288673 | 0.00015425 | 6.364E-7 |
| Convergence criterion (ABSGCONV=0.00001) satisfied. |
The generalized chi-square statistic in the “Fit Statistics” table is small for this model (Output 41.6.6). There is very little residual variation. The radial smoother is associated with 433.55 residual degrees of freedom, computed
as 597 minus the trace of the smoother matrix.
Output 41.6.6: Fit Statistics in Repeated Measures Analysis
| Fit Statistics | |
|---|---|
| -2 Res Log Likelihood | -1886.29 |
| AIC (smaller is better) | -1882.29 |
| AICC (smaller is better) | -1882.27 |
| BIC (smaller is better) | -1879.77 |
| CAIC (smaller is better) | -1877.77 |
| HQIC (smaller is better) | -1881.56 |
| Generalized Chi-Square | 0.47 |
| Gener. Chi-Square / DF | 0.00 |
| Radial Smoother df(res) | 433.55 |
The “Covariance Parameter Estimates” table in Output 41.6.7 displays the estimates of the covariance parameters. The variance of the random spline coefficients is estimated as ![]() , and the scale parameter (=residual variance) estimate is
, and the scale parameter (=residual variance) estimate is ![]() = 0.0008.
= 0.0008.
Output 41.6.7: Estimated Covariance Parameters
| Covariance Parameter Estimates | |||
|---|---|---|---|
| Cov Parm | Subject | Estimate | Standard Error |
| Var[RSmooth(t2)] | cow | 0.5961 | 0.08144 |
| Residual | 0.000800 | 0.000059 | |
The “Type III Tests of Fixed Effects” table displays F tests for the fixed effects in the MODEL statement (Output 41.6.8). There is a strong infection effect as well as the absence of an interaction between infection with M. paratuberculosis and iron dosing. It is important to note, however, that the interpretation of these tests rests on the assumption that the random effects in the mixed model have zero mean; in this case, the radial smoother coefficients.
Output 41.6.8: Tests of Fixed Effects
| Type III Tests of Fixed Effects | ||||
|---|---|---|---|---|
| Effect | Num DF | Den DF | F Value | Pr > F |
| iron | 1 | 358 | 3.59 | 0.0588 |
| infection | 1 | 358 | 21.16 | <.0001 |
| iron*infection | 1 | 358 | 0.09 | 0.7637 |
| tpoint | 1 | 358 | 53.88 | <.0001 |
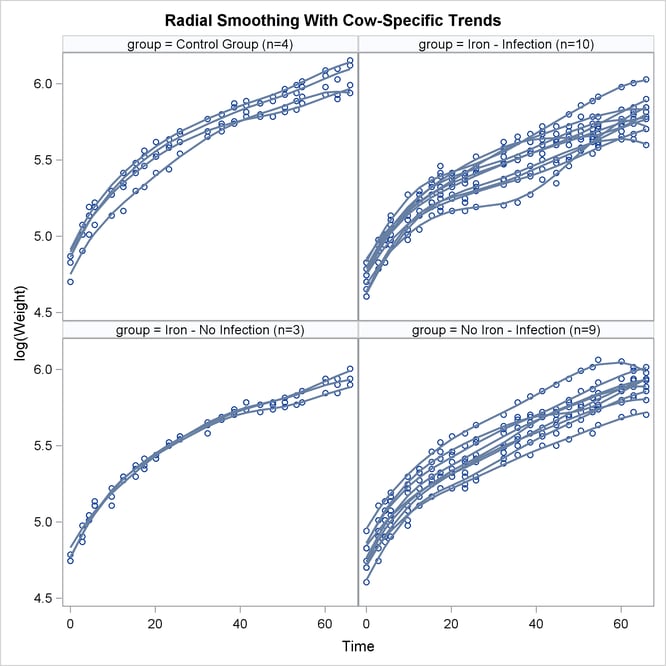
A graph of the observed data and fitted profiles in the four groups is produced with the following statements (Output 41.6.9):
data plot; set gmxout; length group $26; if (iron=0) and (infection=0) then group='Control Group (n=4)'; else if (iron=1) and (infection=0) then group='Iron - No Infection (n=3)'; else if (iron=0) and (infection=1) then group='No Iron - Infection (n=9)'; else group = 'Iron - Infection (n=10)'; run; proc sort data=plot; by group cow; run; proc sgpanel data=plot noautolegend; title 'Radial Smoothing With Cow-Specific Trends'; label tpoint='Time' weight='log(Weight)'; panelby group / columns=2 rows=2; scatter x=tpoint y=weight; series x=tpoint y=pred / group=cow lineattrs=GraphFit; run;
The trends are quite smooth, and you can see how the radial smoother adapts to the cow-specific profile. This is the reason
for the small scale parameter estimate, ![]() . Comparing the panels at the top to the panels at the bottom of Output 41.6.9 reveals the effect of
. Comparing the panels at the top to the panels at the bottom of Output 41.6.9 reveals the effect of Infection. A comparison of the panels on the left to those on the right indicates the weak Iron effect.
The smoothing parameter in this analysis is related to the covariance parameter estimates. Because there is only one radial
smoothing variance component, the amount of smoothing is the same in all four treatment groups. To test whether the smoothing
parameter should be varied by group, you can refine the analysis of the previous model. The following statements fit the same
general model, but they vary the covariance parameters by the levels of the Iron*Infection interaction. This is accomplished with the GROUP= option in the RANDOM statement.
ods select OptInfo FitStatistics CovParms;
proc glimmix data=cows;
t2 = tpoint / 100;
class cow iron infection;
model weight = iron infection iron*infection tpoint;
random t2 / type=rsmooth
subject=cow
group=iron*infection
knotmethod=kdtree(bucket=100);
nloptions tech=newrap;
run;
All observations that have the same value combination of the Iron and Infection effects share the same covariance parameter. As a consequence, you obtain different smoothing parameters result in the four
groups.
In Output 41.6.10, the “Optimization Information” table shows that there are now four covariance parameters in the optimization, one spline coefficient variance for each group.
Output 41.6.10: Analysis with Group-Specific Smoothing Parameter
| Optimization Information | |
|---|---|
| Optimization Technique | Newton-Raphson |
| Parameters in Optimization | 4 |
| Lower Boundaries | 4 |
| Upper Boundaries | 0 |
| Fixed Effects | Profiled |
| Residual Variance | Profiled |
| Starting From | Data |
| Fit Statistics | |
|---|---|
| -2 Res Log Likelihood | -1887.95 |
| AIC (smaller is better) | -1877.95 |
| AICC (smaller is better) | -1877.85 |
| BIC (smaller is better) | -1871.66 |
| CAIC (smaller is better) | -1866.66 |
| HQIC (smaller is better) | -1876.14 |
| Generalized Chi-Square | 0.48 |
| Gener. Chi-Square / DF | 0.00 |
| Radial Smoother df(res) | 434.72 |
| Covariance Parameter Estimates | ||||
|---|---|---|---|---|
| Cov Parm | Subject | Group | Estimate | Standard Error |
| Var[RSmooth(t2)] | cow | iron*infection 0 0 | 0.4788 | 0.1922 |
| Var[RSmooth(t2)] | cow | iron*infection 0 1 | 0.5152 | 0.1182 |
| Var[RSmooth(t2)] | cow | iron*infection 1 0 | 0.4904 | 0.2195 |
| Var[RSmooth(t2)] | cow | iron*infection 1 1 | 0.7105 | 0.1409 |
| Residual | 0.000807 | 0.000060 | ||
Varying this variance component by groups has changed the –2 Res Log Likelihood from –1886.29 to –1887.95 (Output 41.6.10). The difference, 1.66, can be viewed (asymptotically) as the realization of a chi-square random variable with three degrees of freedom. The difference is not significant (p = 0.64586). The “Covariance Parameter Estimates” table confirms that the estimates of the spline coefficient variance are quite similar in the four groups, ranging from 0.4788 to 0.7105.
Finally, you can apply a different technique for varying the temporal trends among the cows. From Output 41.6.9 it appears that an assumption of parallel trends within groups might be reasonable. In other words, you can fit a model in which the “overall” trend over time in each group is modeled nonparametrically, and this trend is shifted up or down to capture the behavior of the individual cow. You can accomplish this with the following statements:
ods select FitStatistics CovParms;
proc glimmix data=cows;
t2 = tpoint / 100;
class cow iron infection;
model weight = iron infection iron*infection tpoint;
random t2 / type=rsmooth
subject=iron*infection
knotmethod=kdtree(bucket=100);
random intercept / subject=cow;
output out=gmxout pred(blup)=pred;
nloptions tech=newrap;
run;
There are now two subject effects in this analysis. The first RANDOM statement applies the radial smoothing and identifies the experimental conditions as the subject. For each condition, a separate realization of the random spline coefficients is obtained. The second RANDOM statement adds a random intercept to the trend for each cow. This random intercept results in the parallel shift of the trends over time.
Results from this analysis are shown in Output 41.6.11.
Output 41.6.11: Analysis with Parallel Shifts
| Fit Statistics | |
|---|---|
| -2 Res Log Likelihood | -1788.52 |
| AIC (smaller is better) | -1782.52 |
| AICC (smaller is better) | -1782.48 |
| BIC (smaller is better) | -1788.52 |
| CAIC (smaller is better) | -1785.52 |
| HQIC (smaller is better) | -1788.52 |
| Generalized Chi-Square | 1.17 |
| Gener. Chi-Square / DF | 0.00 |
| Radial Smoother df(res) | 547.21 |
| Covariance Parameter Estimates | |||
|---|---|---|---|
| Cov Parm | Subject | Estimate | Standard Error |
| Var[RSmooth(t2)] | iron*infection | 0.5398 | 0.1940 |
| Intercept | cow | 0.007122 | 0.002173 |
| Residual | 0.001976 | 0.000121 | |
Because the parallel shift model is not nested within either one of the previous models, the models cannot be compared with a likelihood ratio test. However, you can draw on the other fit statistics.
All statistics indicate that this model does not fit the data as well as the initial model that varies the spline coefficients by cow. The Pearson chi-square statistic is more than twice as large as in the previous model, indicating much more residual variation in the fit. On the other hand, this model generates only four sets of spline coefficients, one for each treatment group, and thus retains more residual degrees of freedom.
The “Covariance Parameter Estimates” table in Output 41.6.11 displays the solutions for the covariance parameters. The estimate of the variance of the spline coefficients is not that different from the estimate obtained in the first model (0.5961). The residual variance, however, has more than doubled.
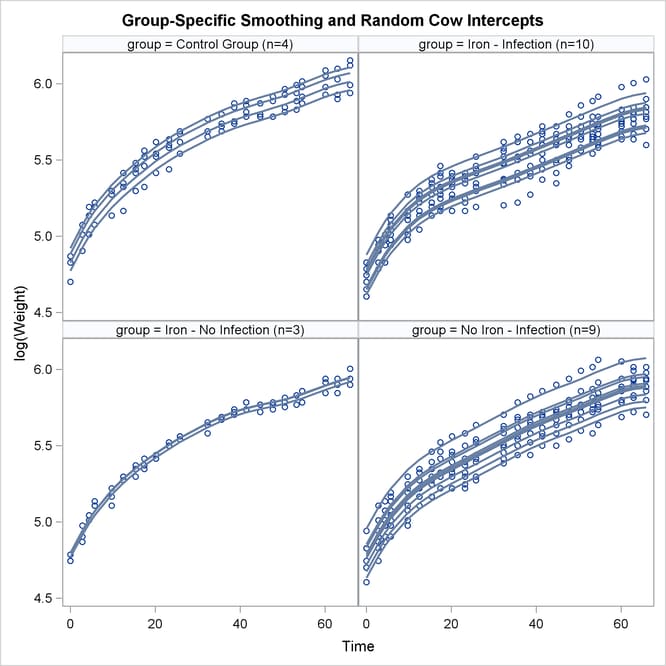
Using similar SAS statements as previously, you can produce a plot of the observed and predicted profiles (Output 41.6.12).
The parallel shifts of the nonparametric smooths are clearly visible in Output 41.6.12. In the groups receiving only iron or only an infection, the parallel lines assumption holds quite well. In the control group and the group receiving iron and the infection, the parallel shift assumption does not hold as well. Two of the profiles in the iron-only group are nearly indistinguishable.
This example demonstrates that mixed model smoothing techniques can be applied not only to achieve scatter plot smoothing, but also to longitudinal or repeated measures data. You can then use the SUBJECT= option in the RANDOM statement to obtain independent sets of spline coefficients for different subjects, and the GROUP= option in the RANDOM statement to vary the degree of smoothing across groups. Also, radial smoothers can be combined with other random effects. For the data considered here, the appropriate model is one with a single smoothing parameter for all treatment group and cow-specific spline coefficients.