The GLIMMIX Procedure

One- and Two-Sided Testing, Mixture Distributions

Consider testing the hypothesis $H_0\colon \theta _ i = 0$ . If $\Omega$ is the open interval $(0, \infty )$ , then only a one-sided alternative hypothesis is meaningful,

$H_0\colon \theta _ i = 0 \quad H_ a\colon \theta _ i > 0$

This is the appropriate set of hypotheses, for example, when $\theta _ i$ is the variance of a G-side random effect. The positivity constraint on $\Omega$ is required for valid conditional and marginal distributions of the data. Verbeke and Molenberghs (2003) refer to this situation as the constrained case.

However, if one focuses on the validity of the marginal distribution alone, then negative values for $\theta _ i$ might be permissible, provided that the marginal variance remains positive definite. In the vernacular or Verbeke and Molenberghs (2003), this is the unconstrained case. The appropriate alternative hypothesis is then two-sided,

$H_0\colon \theta _ i = 0 \quad H_ a\colon \theta _ i \not= 0$

Several important issues are connected to the choice of hypotheses. The GLIMMIX procedure by default imposes constraints on some covariance parameters. For example, variances and scale parameters have a lower bound of 0. This implies a constrained setting with one-sided alternatives. If you specify the NOBOUND option in the PROC GLIMMIX statement, or the NOBOUND option in the PARMS statement, the boundary restrictions are lifted from the covariance parameters and the GLIMMIX procedure takes an unconstrained stance in the sense of Verbeke and Molenberghs (2003). The alternative hypotheses for variance components are then two-sided.

When $H_0\colon \theta _ i = 0$ and $\Omega = (0,\infty )$ , the value of $\theta _ i$ under the null hypothesis is on the boundary of the parameter space. The distribution of the likelihood ratio test statistic $\lambda$ is then nonstandard. In general, it is a mixture of distributions, and in certain special cases, it is a mixture of central chi-square distributions. Important contributions to the understanding of the asymptotic behavior of the likelihood ratio and score test statistic in this situation have been made by, for example, Self and Liang (1987); Shapiro (1988); Silvapulle and Silvapulle (1995). Stram and Lee (1994, 1995) applied the results of Self and Liang (1987) to likelihood ratio testing in the mixed model with uncorrelated errors. Verbeke and Molenberghs (2003) compared the score and likelihood ratio tests in random effects models with unstructured $\bG$ matrix and provide further results on mixture distributions.

The GLIMMIX procedure recognizes the following special cases in the computation of p-values ( $\widehat{\lambda }$ denotes the realized value of the test statistic). Notice that the probabilities of general chi-square mixture distributions do not equal linear combination of central chi-square probabilities (Davis 1977; Johnson, Kotz, and Balakrishnan 1994, Section 18.8).

$\nu$ parameters are tested, and neither parameters specified under 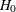nor nuisance parameters are on the boundary of the parameters space (Case 4 in Self and Liang 1987). The p-value is computed by the classical result:

$p = \mr {Pr} \left(\chi ^2_\nu \geq \widehat{\lambda } \right)$
One parameter is specified under 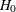and it falls on the boundary. No other parameters are on the boundary (Case 5 in Self and Liang 1987).

$p = \left\{ \begin{array}{ll} 1 & \widehat{\lambda } = 0 \\ 0.5 \, \mr {Pr} \left(\chi ^2_1 \geq \widehat{\lambda }\right) & \widehat{\lambda } > 0 \end{array} \right.$

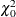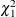Note that this implies a 50:50 mixture of a $\chi ^2_0$ and a $\chi ^2_1$ distribution. This is also Case 1 in Verbeke and Molenberghs (2000, p. 69).
Two parameters are specified under 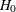, and one falls on the boundary. No nuisance parameters are on the boundary (Case 6 in Self and Liang 1987).

$p = 0.5 \, \mr {Pr} \left(\chi ^2_1 \geq \widehat{\lambda }\right) + 0.5 \, \mr {Pr} \left(\chi ^2_2 \geq \widehat{\lambda }\right)$

A special case of this scenario is the addition of a random effect to a model with a single random effect and unstructured covariance matrix (Case 2 in Verbeke and Molenberghs 2000, p. 70).
Removing j random effects from 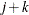uncorrelated random effects (Verbeke and Molenberghs, 2003).

$p = 2^{-j} \sum _{i=0}^ j \left(\begin{array}{c} j \\ i \end{array}\right) \mr {Pr} \left(\chi ^2_ i \geq \widehat{\lambda } \right)$

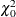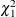Note that this case includes the case of testing a single random effects variance against zero, which leads to a 50:50 mixture of a $\chi ^2_0$ and a $\chi ^2_1$ as in 2.
Removing a random effect from an unstructured 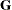$\bG$ matrix (Case 3 in Verbeke and Molenberghs 2000, p. 71).

$p = 0.5 \, \mr {Pr} \left( \chi ^2_ k \geq \widehat{\lambda } \right) + 0.5 \, \mr {Pr} \left( \chi ^2_{k-1} \geq \widehat{\lambda } \right)$

where k is the number of random effects (columns of 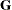$\bG$ ) in the full model. Case 5 in Self and Liang (1987) describes a special case.

When the GLIMMIX procedure determines that estimates of nuisance parameters (parameters not specified under ) fall on the boundary, no mixture results are computed.

You can request that the procedure not use mixtures with the CLASSICAL option in the COVTEST statement. If mixtures are used, the Note column of the “Likelihood Ratio Tests of Covariance Parameters” table contains the “MI” entry. The “DF” entry is used when PROC GLIMMIX determines that the standard computation of p-values is appropriate. The “–” entry is used when the classical computation was used because the testing and model scenario does not match one of the special cases described previously.