The SURVEYMEANS Procedure
Fay’s BRR Method
Fay’s method is a modification of the BRR method, and it requires a stratified sample design with two primary sampling units (PSUs) per stratum. The total number of replicates R is the smallest multiple of 4 that is greater than the total number of strata H. However, if you prefer a larger number of replicates, you can specify the REPS= method-option.
For each replicate, Fay’s method uses a Fay coefficient ![]() to impose a perturbation of the original weights in the full sample that is gentler than using only half-samples, as in the
traditional BRR method. The Fay coefficient
to impose a perturbation of the original weights in the full sample that is gentler than using only half-samples, as in the
traditional BRR method. The Fay coefficient ![]() can be set by specifying the FAY =
can be set by specifying the FAY = ![]() method-option. By default,
method-option. By default, ![]() if the FAY method-option is specified without providing a value for
if the FAY method-option is specified without providing a value for ![]() (Judkins, 1990; Rao and Shao, 1999). When
(Judkins, 1990; Rao and Shao, 1999). When ![]() , Fay’s method becomes the traditional BRR method. For more details, see Dippo, Fay, and Morganstein (1984); Fay (1984, 1989); Judkins (1990).
, Fay’s method becomes the traditional BRR method. For more details, see Dippo, Fay, and Morganstein (1984); Fay (1984, 1989); Judkins (1990).
Let H be the number of strata. Replicates are constructed by using the first H columns of the ![]() Hadamard matrix, where R is the number of replicates,
Hadamard matrix, where R is the number of replicates, ![]() . The rth (
. The rth (![]() ) replicate is created from the full sample according to the rth row of the Hadamard matrix as follows:
) replicate is created from the full sample according to the rth row of the Hadamard matrix as follows:
-
If the
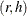 element of the Hadamard matrix is 1, then the full sample weight of the first PSU in stratum h is multiplied by
element of the Hadamard matrix is 1, then the full sample weight of the first PSU in stratum h is multiplied by  and the full sample weight of the second PSU is multiplied by
and the full sample weight of the second PSU is multiplied by 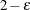 to obtain the rth replicate weights.
to obtain the rth replicate weights.
-
If the
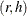 element of the Hadamard matrix is –1, then the full sample weight of the first PSU in stratum h is multiplied by
element of the Hadamard matrix is –1, then the full sample weight of the first PSU in stratum h is multiplied by 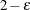 and the full sample weight of the second PSU is multiplied by
and the full sample weight of the second PSU is multiplied by  to obtain the rth replicate weights.
to obtain the rth replicate weights.
You can use the VARMETHOD=BRR(OUTWEIGHTS=) method-option to save the replicate weights into a SAS data set.
By default, an appropriate Hadamard matrix is generated automatically to create the replicates. You can request that the Hadamard matrix be displayed by specifying the VARMETHOD=BRR(PRINTH) method-option. If you provide a Hadamard matrix by specifying the VARMETHOD=BRR(HADAMARD=) method-option, then the replicates are generated according to the provided Hadamard matrix.
Suppose that ![]() is a population parameter of interest. Let
is a population parameter of interest. Let ![]() be the estimate from the full sample for
be the estimate from the full sample for ![]() . Let
. Let ![]() be the estimate from the rth replicate subsample by using replicate weights. PROC SURVEYMEANS estimates the variance of
be the estimate from the rth replicate subsample by using replicate weights. PROC SURVEYMEANS estimates the variance of ![]() by
by
|
|
with H degrees of freedom, where H is the number of strata.
