The ROBUSTREG Procedure
High-Breakdown-Value Estimation
The breakdown value of an estimator is defined as the smallest fraction of contamination that can cause the estimator to take on values that are arbitrarily far from its value on the uncontaminated data. The breakdown value of an estimator can be used as a measure of the robustness of the estimator. Rousseeuw and Leroy (1987) and others introduced the following high-breakdown-value estimators for linear regression.
LTS Estimate
The least trimmed squares (LTS) estimate proposed by Rousseeuw (1984) is defined as the p-vector
|
|
where ![]() are the ordered squared residuals
are the ordered squared residuals ![]() ,
, ![]() , and h is defined in the range
, and h is defined in the range ![]() .
.
You can specify the parameter h with the H= option in the PROC ROBUSTREG statement. By default, ![]() . The breakdown value is
. The breakdown value is ![]() for the LTS estimate.
for the LTS estimate.
The ROBUSTREG procedure computes LTS estimates by using the FAST-LTS algorithm of Rousseeuw and Van Driessen (2000). The estimates are often used to detect outliers in the data, which are then downweighted in the resulting weighted LS regression.
Algorithm
Least trimmed squares (LTS) regression is based on the subset of h observations (out of a total of n observations) whose least squares fit possesses the smallest sum of squared residuals. The coverage h can be set between ![]() and n. The LTS method was proposed by Rousseeuw (1984, p. 876) as a highly robust regression estimator with breakdown value
and n. The LTS method was proposed by Rousseeuw (1984, p. 876) as a highly robust regression estimator with breakdown value ![]() . The ROBUSTREG procedure uses the FAST-LTS algorithm given by Rousseeuw and Van Driessen (2000). The intercept adjustment technique is also used in this implementation. However, because this adjustment is expensive to
compute, it is optional. You can use the IADJUST= option in the PROC ROBUSTREG statement to request or suppress the intercept
adjustment. By default, PROC ROBUSTREG does intercept adjustment for data sets with fewer than 10,000 observations. The steps
of the algorithm are described briefly as follows. See Rousseeuw and Van Driessen (2000) for details.
. The ROBUSTREG procedure uses the FAST-LTS algorithm given by Rousseeuw and Van Driessen (2000). The intercept adjustment technique is also used in this implementation. However, because this adjustment is expensive to
compute, it is optional. You can use the IADJUST= option in the PROC ROBUSTREG statement to request or suppress the intercept
adjustment. By default, PROC ROBUSTREG does intercept adjustment for data sets with fewer than 10,000 observations. The steps
of the algorithm are described briefly as follows. See Rousseeuw and Van Driessen (2000) for details.
-
The default h is
![$[{3n+p+1 \over 4}]$](images/statug_rreg0123.png) , where p is the number of independent variables. You can specify any integer h with
, where p is the number of independent variables. You can specify any integer h with ![$[{n \over 2}] + 1 \leq h \leq [{3n+p+1 \over 4}]$](images/statug_rreg0124.png) with the H= option in the MODEL statement. The breakdown value for LTS,
with the H= option in the MODEL statement. The breakdown value for LTS, 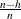 , is reported. The default h is a good compromise between breakdown value and statistical efficiency.
, is reported. The default h is a good compromise between breakdown value and statistical efficiency.
-
If p = 1 (single regressor), the procedure uses the exact algorithm of Rousseeuw and Leroy (1987, p. 172).
-
If
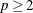 , PROC ROBUSTREG uses the following algorithm. If n < 2 ssubs, where ssubs is the size of the subgroups (you can specify ssubs by using the SUBGROUPSIZE= option in the PROC ROBUSTREG statement; by default, ssubs = 300), PROC ROBUSTREG draws a random p-subset and computes the regression coefficients by using these p points (if the regression is degenerate, another p-subset is drawn). The absolute residuals for all observations in the data set are computed, and the first h points with smallest absolute residuals are selected. From this selected h-subset, PROC ROBUSTREG carries out nsteps C-steps (concentration steps; see Rousseeuw and Van Driessen (2000) for details). You can specify nsteps with the CSTEP= option in the PROC ROBUSTREG statement; by default, nsteps = 2. PROC ROBUSTREG redraws p-subsets and repeats the preceding computation nrep times, and then finds the nbsol (at most) solutions with the lowest sums of h squared residuals. You can specify nrep with the NREP= option in the PROC ROBUSTREG statement; by default, NREP=
, PROC ROBUSTREG uses the following algorithm. If n < 2 ssubs, where ssubs is the size of the subgroups (you can specify ssubs by using the SUBGROUPSIZE= option in the PROC ROBUSTREG statement; by default, ssubs = 300), PROC ROBUSTREG draws a random p-subset and computes the regression coefficients by using these p points (if the regression is degenerate, another p-subset is drawn). The absolute residuals for all observations in the data set are computed, and the first h points with smallest absolute residuals are selected. From this selected h-subset, PROC ROBUSTREG carries out nsteps C-steps (concentration steps; see Rousseeuw and Van Driessen (2000) for details). You can specify nsteps with the CSTEP= option in the PROC ROBUSTREG statement; by default, nsteps = 2. PROC ROBUSTREG redraws p-subsets and repeats the preceding computation nrep times, and then finds the nbsol (at most) solutions with the lowest sums of h squared residuals. You can specify nrep with the NREP= option in the PROC ROBUSTREG statement; by default, NREP=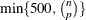 . For small n and p, all
. For small n and p, all 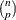 subsets are used and the NREP= option is ignored (Rousseeuw and Hubert, 1996). You can specify nbsol with the NBEST= option in the PROC ROBUSTREG statement; by default, NBEST=10. For each of these nbsol best solutions, C-steps are taken until convergence and the best final solution is found.
subsets are used and the NREP= option is ignored (Rousseeuw and Hubert, 1996). You can specify nbsol with the NBEST= option in the PROC ROBUSTREG statement; by default, NBEST=10. For each of these nbsol best solutions, C-steps are taken until convergence and the best final solution is found.
-
If
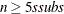 , construct five disjoint random subgroups with size ssubs. If
, construct five disjoint random subgroups with size ssubs. If 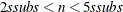 , the data are split into at most four subgroups with ssubs or more observations in each subgroup, so that each observation belongs to a subgroup and the subgroups have roughly the
same size. Let nsubs denote the number of subgroups. Inside each subgroup, PROC ROBUSTREG repeats the step 3 algorithm nrep / nsubs times, keeps the nbsol best solutions, and pools the subgroups, yielding the merged set of size
, the data are split into at most four subgroups with ssubs or more observations in each subgroup, so that each observation belongs to a subgroup and the subgroups have roughly the
same size. Let nsubs denote the number of subgroups. Inside each subgroup, PROC ROBUSTREG repeats the step 3 algorithm nrep / nsubs times, keeps the nbsol best solutions, and pools the subgroups, yielding the merged set of size 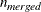 . In the merged set, for each of the
. In the merged set, for each of the 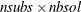 best solutions, nsteps C-steps are carried out by using
best solutions, nsteps C-steps are carried out by using 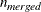 and
and ![$h_{\mathit{merged}} = [n_{\mathit{merged}}{h \over n}]$](images/statug_rreg0132.png) and the nbsol best solutions are kept. In the full data set, for each of these nbsol best solutions, C-steps are taken by using n and h until convergence and the best final solution is found.
and the nbsol best solutions are kept. In the full data set, for each of these nbsol best solutions, C-steps are taken by using n and h until convergence and the best final solution is found.
Note: At step 3 in the algorithm, a randomly selected p-subset might be degenerate (that is, its design matrix might be singular). If the total number of p-subsets from any subgroup is more than 4,000 and the ratio of degenerate p-subsets is more than the threshold specified in FAILRATIO= option, the algorithm is terminated with an error message.
R-Square
The robust version of R-square for the LTS estimate is defined as
|
|
for models with the intercept term and as
|
|
for models without the intercept term, where
![\[ s_{\mathit{LTS}}(\bX ,\mb {y}) = d_{h,n} \sqrt { {1\over h} \sum _{i=1}^ h r^2_{(i)} } \]](images/statug_rreg0135.png) |
Note that ![]() is a preliminary estimate of the parameter
is a preliminary estimate of the parameter ![]() in the distribution function
in the distribution function ![]() .
.
Here ![]() is chosen to make
is chosen to make ![]() consistent, assuming a Gaussian model. Specifically,
consistent, assuming a Gaussian model. Specifically,
|
|
|
|
|
|
|
|
with ![]() and
and ![]() being the distribution function and the density function of the standard normal distribution, respectively.
being the distribution function and the density function of the standard normal distribution, respectively.
Final Weighted Scale Estimator
The ROBUSTREG procedure displays two scale estimators, ![]() and Wscale. The estimator Wscale is a more efficient scale estimator based on the preliminary estimate
and Wscale. The estimator Wscale is a more efficient scale estimator based on the preliminary estimate ![]() ; it is defined as
; it is defined as
|
|
where
|
|
You can specify k with the CUTOFF= option in the MODEL statement. By default, k = 3.
S Estimate
The S estimate proposed by Rousseeuw and Yohai (1984) is defined as the p-vector
|
|
where the dispersion ![]() is the solution of
is the solution of
|
|
Here ![]() is set to
is set to ![]() such that
such that ![]() and
and ![]() are asymptotically consistent estimates of
are asymptotically consistent estimates of ![]() and
and ![]() for the Gaussian regression model. The breakdown value of the S estimate is
for the Gaussian regression model. The breakdown value of the S estimate is
|
|
The ROBUSTREG procedure provides two choices for ![]() : Tukey’s bisquare function and Yohai’s optimal function.
: Tukey’s bisquare function and Yohai’s optimal function.
Tukey’s bisquare function, which you can specify with the option CHIF=TUKEY, is
|
|
The constant ![]() controls the breakdown value and efficiency of the S estimate. If you specify the efficiency by using the EFF= option, you
can determine the corresponding
controls the breakdown value and efficiency of the S estimate. If you specify the efficiency by using the EFF= option, you
can determine the corresponding ![]() . The default
. The default ![]() is 2.9366 such that the breakdown value of the S estimate is 0.25 with a corresponding asymptotic efficiency for the Gaussian
model of 75.9%.
is 2.9366 such that the breakdown value of the S estimate is 0.25 with a corresponding asymptotic efficiency for the Gaussian
model of 75.9%.
The Yohai function, which you can specify with the option CHIF=YOHAI, is
![\[ \chi _{k_0}(s) = \left\{ \begin{array}{lll} {s^2 \over 2} & {\mbox{if }} |s| \leq 2 k_0 \\ k_0^2 [ b_0 + b_1({s\over k_0})^2 + b_2({s\over k_0})^4 & \\ + b_3({s\over k_0})^6 + b_4({s\over k_0})^8] & {\mbox{if }} 2 k_0 < |s| \leq 3 k_0\\ 3.25 k_0^2 & {\mbox{if }} |s| >3 k_0 \end{array} \right. \]](images/statug_rreg0156.png) |
where ![]() ,
, ![]() ,
, ![]() ,
, ![]() , and
, and ![]() . If you specify the efficiency by using the EFF= option, you can determine the corresponding
. If you specify the efficiency by using the EFF= option, you can determine the corresponding ![]() . By default,
. By default, ![]() is set to 0.7405 such that the breakdown value of the S estimate is 0.25 with a corresponding asymptotic efficiency for the
Gaussian model of 72.7%.
is set to 0.7405 such that the breakdown value of the S estimate is 0.25 with a corresponding asymptotic efficiency for the
Gaussian model of 72.7%.
Algorithm
The ROBUSTREG procedure implements the algorithm by Marazzi (1993) for the S estimate, which is a refined version of the algorithm proposed by Ruppert (1992). The refined algorithm is briefly described as follows.
Initialize iter = 1.
-
Draw a random q-subset of the total n observations and compute the regression coefficients by using these q observations (if the regression is degenerate, draw another q-subset), where
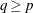 can be specified with the SUBSIZE= option. By default,
can be specified with the SUBSIZE= option. By default, 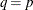 .
.
-
Compute the residuals:
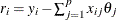 for
for 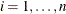 . If iter = 1, set
. If iter = 1, set 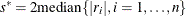 ; if
; if 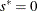 , set
, set 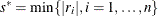 ; else while
; else while 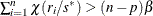 , set
, set 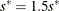 ; go to step 3. If iter > 1 and
; go to step 3. If iter > 1 and 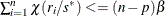 , go to step 3; otherwise, go to step 5.
, go to step 3; otherwise, go to step 5.
-
Solve for s the equation
![\[ {1\over n-p} \sum _{i=1}^ n \chi (r_ i / s)= \beta \]](images/statug_rreg0171.png)
using an iterative algorithm.
-
If iter > 1 and
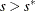 , go to step 5. Otherwise, set
, go to step 5. Otherwise, set 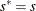 and
and 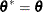 . If
. If 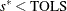 , return
, return 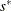 and
and 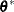 ; otherwise, go to step 5.
; otherwise, go to step 5.
-
If iter < NREP, set
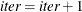 and return to step 1; otherwise, return
and return to step 1; otherwise, return 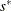 and
and 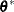 .
.
The ROBUSTREG procedure does the following refinement step by default. You can request that this refinement not be done by using the NOREFINE option in the PROC ROBUSTREG statement.
-
Let
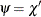 . Using the values
. Using the values 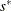 and
and 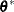 from the previous steps, compute M estimates
from the previous steps, compute M estimates 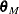 and
and 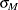 of
of 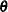 and
and  with the setup for M estimation that is described in the section M Estimation. If
with the setup for M estimation that is described in the section M Estimation. If 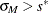 , give a warning and return
, give a warning and return 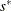 and
and 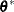 ; otherwise, return
; otherwise, return 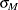 and
and 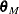 .
.
You can specify TOLS with the TOLERANCE= option; by default, TOLERANCE=0.001. Alternately, you can specify NREP with the NREP= option. You can also use the options NREP=NREP0 or NREP=NREP1 to determine NREP according to the following table. NREP=NREP0 is set as the default.
Table 80.10: Default NREP
|
P |
NREP0 |
NREP1 |
|---|---|---|
|
1 |
150 |
500 |
|
2 |
300 |
1000 |
|
3 |
400 |
1500 |
|
4 |
500 |
2000 |
|
5 |
600 |
2500 |
|
6 |
700 |
3000 |
|
7 |
850 |
3000 |
|
8 |
1250 |
3000 |
|
9 |
1500 |
3000 |
|
>9 |
1500 |
3000 |
Note: At step 1 in the algorithm, a randomly selected q-subset might be degenerate. If the total number of q-subsets from any subgroup is more than 4,000 and the ratio of degenerate q-subsets is more than the threshold specified in FAILRATIO= option, the algorithm is terminated with an error message.
R-Square and Deviance
The robust version of R-square for the S estimate is defined as
|
|
for the model with the intercept term and
|
|
for the model without the intercept term, where ![]() is the S estimate of the scale in the full model,
is the S estimate of the scale in the full model, ![]() is the S estimate of the scale in the regression model with only the intercept term, and
is the S estimate of the scale in the regression model with only the intercept term, and ![]() is the S estimate of the scale without any regressor. The deviance D is defined as the optimal value of the objective function on the
is the S estimate of the scale without any regressor. The deviance D is defined as the optimal value of the objective function on the ![]() scale:
scale:
|
|
Asymptotic Covariance and Confidence Intervals
Since the S estimate satisfies the first-order necessary conditions as the M estimate, it has the same asymptotic covariance as that of the M estimate. All three estimators of the asymptotic covariance for the M estimate in the section Asymptotic Covariance and Confidence Intervals can be used for the S estimate. Besides, the weighted covariance estimator H4 described in the section Asymptotic Covariance and Confidence Intervals is also available and is set as the default. Confidence intervals for estimated parameters are computed from the diagonal elements of the estimated asymptotic covariance matrix.
