The QUANTREG Procedure
ODS Graphics
Statistical procedures use ODS Graphics to create graphs as part of their output. ODS Graphics is described in detail in Chapter 21: Statistical Graphics Using ODS.
Before you create graphs, ODS Graphics must be enabled (for example, by specifying the ODS GRAPHICS ON statement). For more information about enabling and disabling ODS Graphics, see the section Enabling and Disabling ODS Graphics in Chapter 21: Statistical Graphics Using ODS.
The overall appearance of graphs is controlled by ODS styles. Styles and other aspects of using ODS Graphics are discussed in the section A Primer on ODS Statistical Graphics in Chapter 21: Statistical Graphics Using ODS.
For a single quantile, two plots are particularly useful in revealing outliers and leverage points. The first is a scatter plot of the standardized residuals for the specified quantile against the robust distances. The second is a scatter plot of the robust distances against the classical Mahalanobis distances. You can request these two plots by using the PLOT=RDPLOT and PLOT=DDPLOT options.
You can also request a normal quantile-quantile plot and a histogram of the standardized residuals for the specified quantile with the PLOT=QQPLOT and PLOT=HISTOGRAM options, respectively.
You can request a plot of fitted conditional quantiles by the single continuous variable specified in the model with the PLOT=FITPLOT option.
All these plots can be requested by specifying corresponding plot options in either the PROC QUANTREG statement or the MODEL statement. If you specify same plot options in both statements, options in the PROC QUANTREG statement override options in the MODEL statement.
You can specify the PLOT=QUANTPLOT option in only the MODEL statement to request a quantile process plot with confidence bands.
The plot options in the PROC QUANTREG statement and the MODEL statement are summarized in Table 77.10. See the PLOT= option in the PROC QUANTREG statement and the PLOT= option in the MODEL statement for details.
Table 77.10: Options for Plots
|
Keyword |
Plot |
|
|---|---|---|
|
ALL |
All appropriate plots |
|
|
DDPLOT |
Robust distance vs. Mahalanobis distance |
|
|
FITPLOT |
Conditional quantile fit vs. independent variable |
|
|
HISTOGRAM |
Histogram of standardized robust residuals |
|
|
NONE |
No plot |
|
|
QUANTPLOT |
Scatter plot of regression quantile |
|
|
QQPLOT |
Q-Q plot of standardized robust residuals |
|
|
RDPLOT |
Standardized robust residual vs. robust distance |
The following subsections provide information about these graphs.
ODS Graph Names
The QUANTREG procedure assigns a name to each graph it creates. You can use these names to reference the graphs when using ODS. The names along with the required statements and options are listed in Table 77.11.
Table 77.11: Graphs Produced by PROC QUANTREG
|
ODS Graph Name |
Plot Description |
Statement |
Option |
|---|---|---|---|
|
DDPlot |
Robust distance versus Mahalanobis distance |
PROC MODEL |
DDPLOT |
|
FitPlot |
Quantile fit versus independent variable |
PROC MODEL |
FITPLOT |
|
Histogram |
Histogram of standardized robust residuals |
PROC MODEL |
HISTOGRAM |
|
QQPlot |
Q-Q plot of standardized robust residuals |
PROC MODEL |
QQPLOT |
|
QuantPanel |
Panel of quantile plots with confidence limits |
MODEL |
QUANTPLOT |
|
QuantPlot |
Scatter plot for regression quantiles with confidence limits |
MODEL |
QUANTPLOT UNPACK |
|
RDPlot |
Standardized robust residual versus robust distance |
PROC MODEL |
RDPLOT |
Fit Plot
When the model has a single independent continuous variable (with or without the intercept), the QUANTREG procedure automatically creates a plot of fitted conditional quantiles against this independent variable for one or more quantiles specified in the MODEL statement.
The following example reuses the trout data set in the section Analysis of Fish-Habitat Relationships to show the fit plot for one or several quantiles.
ods graphics on; proc quantreg data=trout ci=resampling; model LnDensity = WDRatio / quantile=0.9 seed=1268; run;
proc quantreg data=trout ci=resampling; model LnDensity = WDRatio / quantile=0.5 0.75 0.9 seed=1268; run;
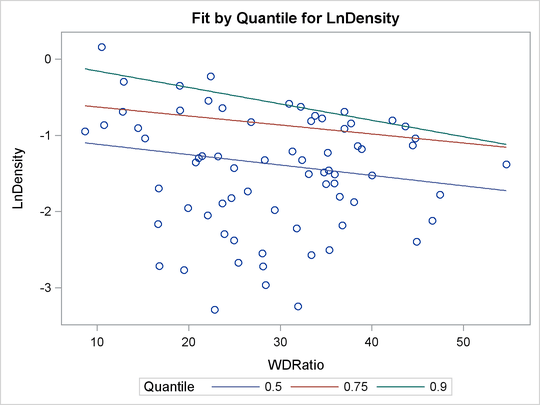
For a single quantile, the confidence limits for the fitted conditional quantiles are also plotted if you specify the CI=RESAMPLING or CI=SPARSITY option. (See Figure 77.14.) For multiple quantiles, confidence limits are not plotted by default. (See Figure 77.15.) You can add the confidence limits on the plot by specifying the option PLOT=FITPLOT(SHOWLIMITS).
The QUANTREG procedure also provides fit plots for quantile regression splines and polynomials if they are based on a single continuous variable. See Example 77.4 and Example 77.5 for some examples.
Figure 77.14: Fit Plot with Confidence Limits
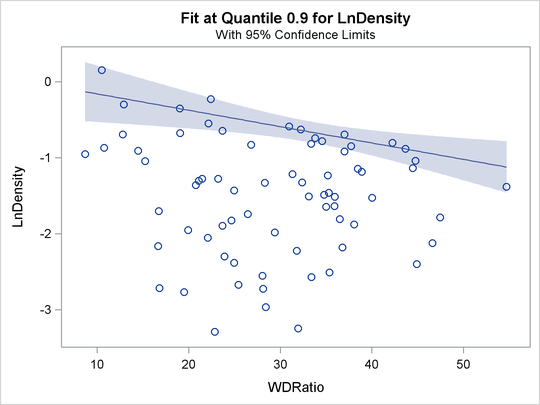
Figure 77.15: Fit Plot for Multiple Quantiles
Quantile Process Plot
A quantile process plot is a scatter plot of an estimated regression parameter against quantile. You can request this plot with the PLOT=QUANTPLOT option in the MODEL statement when multiple regression quantiles or the entire quantile process is computed. Quantile process plots are often used to check model variations at different quantiles, which is usually called model heterogeneity.
By default, panels are used to hold multiple process plots (up to four in each panel). You can use the UNPACK option to request individual process plots. Figure 77.10 in the section Analysis of Fish-Habitat Relationships shows a panel with two quantile process plots. Output 77.2.9 in Example 77.2 shows a single quantile process plot. Example 77.3 demonstrates more quantile process plots and their usage.
Distance-Distance Plot
The distance-distance plot (DDPLOT) is mainly used for leverage-point diagnostics. It is a scatter plot of the robust distances against the classical Mahalanobis distances for the continuous independent variables. See the section Leverage Point and Outlier Detection for details about the robust distance. If there is a classification variable specified in the model, this plot is not created.
You can use the PLOT=DDPLOT option to request this plot. The following statements use the growth data set in Example 77.2 to create a single plot, shown in Output 77.2.4 in Example 77.2:
ods graphics on;
proc quantreg data=growth ci=resampling plot=ddplot;
model GDP = lgdp2 mse2 fse2 fhe2 mhe2 lexp2
lintr2 gedy2 Iy2 gcony2 lblakp2 pol2 ttrad2
/ quantile=.5 diagnostics leverage(cutoff=8) seed=1268;
id Country;
run;
The reference lines represent the cutoff values. The diagonal line is also drawn to show the distribution of the distances. By default, all outliers and leverage points are labeled with observation numbers. To change the default, you can use the LABEL= option as described in Table 77.5.
Residual-Distance Plot
The residual-distance plot (RDPLOT) is used for both outlier and leverage-point diagnostics. It is a scatter plot of the standardized residuals against the robust distances. See the section Leverage Point and Outlier Detection for details about the robust distance. If a classification variable is specified in the model, this plot is not created.
You can use the PLOT=RDPLOT option to request this plot. The following statements use the growth data set in Example 77.2 to create a single plot, shown in Output 77.2.3 in Example 77.2:
ods graphics on;
proc quantreg data=growth ci=resampling plot=rdplot;
model GDP = lgdp2 mse2 fse2 fhe2 mhe2 lexp2
lintr2 gedy2 Iy2 gcony2 lblakp2 pol2 ttrad2
/ quantile=.5 diagnostics leverage(cutoff=8) seed=1268;
id Country;
run;
The reference lines represent the cutoff values. By default, all outliers and leverage points are labeled with observation numbers. To change the default, you can use the LABEL= option as described in Table 77.5.
If you specify ID variables in the ID statement, instead of observation numbers, the values of the first ID variable are used as labels.
Histogram and Q-Q Plot
PROC QUANTREG produces a histogram and a Q-Q plot for the standardized residuals. The histogram is superimposed with a normal
density curve and a kernel density curve. Using the growth data set in Example 77.2, the following statements create the plot shown in Output 77.2.5 in Example 77.2:
ods graphics on;
proc quantreg data=growth ci=resampling plot=histogram;
model GDP = lgdp2 mse2 fse2 fhe2 mhe2 lexp2
lintr2 gedy2 Iy2 gcony2 lblakp2 pol2 ttrad2
/ quantile=.5 diagnostics leverage(cutoff=8) seed=1268;
id Country;
run;
