The PRINQUAL Procedure
- Overview
- Getting Started
-
Syntax

-
Details
 The Three Methods of Variable TransformationUnderstanding How PROC PRINQUAL WorksSplinesMissing ValuesControlling the Number of IterationsPerforming a Principal Component Analysis of Transformed DataUsing the MAC MethodOutput Data SetAvoiding Constant TransformationsConstant VariablesCharacter OPSCORE VariablesREITERATE Option UsagePassive ObservationsComputational ResourcesDisplayed OutputODS Table NamesODS Graphics
The Three Methods of Variable TransformationUnderstanding How PROC PRINQUAL WorksSplinesMissing ValuesControlling the Number of IterationsPerforming a Principal Component Analysis of Transformed DataUsing the MAC MethodOutput Data SetAvoiding Constant TransformationsConstant VariablesCharacter OPSCORE VariablesREITERATE Option UsagePassive ObservationsComputational ResourcesDisplayed OutputODS Table NamesODS Graphics -
Examples

- References
Computational Resources
This section provides information about the computational resources required to run PROC PRINQUAL.
Let
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
-
For the MTV algorithm, more than
![\[ 56m + 8Nm + 8 \left( 6N + (p + k + 2)(p + k + 11) \right) \]](images/statug_prinqual0052.png)
bytes of array space are required.
-
For the MGV and MAC algorithms, more than
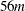 plus the maximum of the data matrix size and the optimal scaling work space bytes of array space are required. The data matrix
size is
plus the maximum of the data matrix size and the optimal scaling work space bytes of array space are required. The data matrix
size is 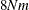 bytes. The optimal scaling work space requires less than
bytes. The optimal scaling work space requires less than 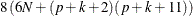 bytes.
bytes.
-
For the MTV and MGV algorithms, more than
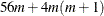 bytes of array space are required.
bytes of array space are required.
-
PROC PRINQUAL tries to store the original and transformed data in memory. If there is not enough memory, a utility data set is used, potentially resulting in a large increase in execution time. The amount of memory for the preceding data formulas is an underestimate of the amount of memory needed to handle most problems. These formulas give an absolute minimum amount of memory required. If a utility data set is used, and if memory could be used with perfect efficiency, then roughly the amount of memory stated previously would be needed. In reality, most problems require at least two or three times the minimum.
-
PROC PRINQUAL sorts the data once. The sort time is roughly proportional to
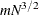 .
.
-
For the MTV algorithm, the time required to compute the variable approximations is roughly proportional to
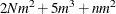 .
.
-
For the MGV algorithm, one regression analysis per iteration is required to compute model parameter estimates. The time required to accumulate the crossproduct matrix is roughly proportional to
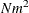 . The time required to compute the regression coefficients is roughly proportional to
. The time required to compute the regression coefficients is roughly proportional to 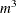 . For each variable for each iteration, the swept crossproduct matrix is updated with time roughly proportional to m(N+m).
The swept crossproduct matrix is updated for each variable with time roughly proportional to
. For each variable for each iteration, the swept crossproduct matrix is updated with time roughly proportional to m(N+m).
The swept crossproduct matrix is updated for each variable with time roughly proportional to 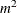 , until computations are refreshed, requiring all sweeps to be performed again.
, until computations are refreshed, requiring all sweeps to be performed again.
-
The only computationally intensive part of the MAC algorithm is the optimal scaling, since variable approximations are simple averages.
-
Each optimal scaling is a multiple regression problem, although some transformations are handled with faster special-case algorithms. The number of regressors for the optimal scaling problems depends on the original values of the variable and the type of transformation. For each monotone spline transformation, an unknown number of multiple regressions is required to find a set of coefficients that satisfies the constraints. The B-spline basis is generated twice for each SPLINE and MSPLINE transformation for each iteration. The time required to generate the B-spline basis is roughly proportional to
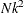 .
.