The PHREG Procedure
- Overview
-
Getting Started

-
Syntax
 PROC PHREG StatementASSESS StatementBASELINE StatementBAYES StatementBY StatementCLASS StatementCONTRAST StatementEFFECT StatementESTIMATE StatementFREQ StatementHAZARDRATIO StatementID StatementLSMEANS StatementLSMESTIMATE StatementMODEL StatementOUTPUT StatementProgramming StatementsRANDOM StatementSTRATA StatementSLICE StatementSTORE StatementTEST StatementWEIGHT Statement
PROC PHREG StatementASSESS StatementBASELINE StatementBAYES StatementBY StatementCLASS StatementCONTRAST StatementEFFECT StatementESTIMATE StatementFREQ StatementHAZARDRATIO StatementID StatementLSMEANS StatementLSMESTIMATE StatementMODEL StatementOUTPUT StatementProgramming StatementsRANDOM StatementSTRATA StatementSLICE StatementSTORE StatementTEST StatementWEIGHT Statement -
Details
 Failure Time DistributionTime and CLASS Variables UsagePartial Likelihood Function for the Cox ModelCounting Process Style of InputLeft-Truncation of Failure TimesThe Multiplicative Hazards ModelThe Frailty ModelHazard RatiosProportional Rates/Means Models for Recurrent EventsNewton-Raphson MethodFirth’s Modification for Maximum Likelihood EstimationRobust Sandwich Variance EstimateTesting the Global Null HypothesisType 3 TestsConfidence Limits for a Hazard RatioUsing the TEST Statement to Test Linear HypothesesAnalysis of Multivariate Failure Time DataModel Fit StatisticsResidualsDiagnostics Based on Weighted ResidualsInfluence of Observations on Overall Fit of the ModelSurvivor Function EstimatorsEffect Selection MethodsAssessment of the Proportional Hazards ModelThe Penalized Partial Likelihood Approach for Fitting Frailty ModelsSpecifics for Bayesian AnalysisComputational ResourcesInput and Output Data SetsDisplayed OutputODS Table NamesODS Graphics
Failure Time DistributionTime and CLASS Variables UsagePartial Likelihood Function for the Cox ModelCounting Process Style of InputLeft-Truncation of Failure TimesThe Multiplicative Hazards ModelThe Frailty ModelHazard RatiosProportional Rates/Means Models for Recurrent EventsNewton-Raphson MethodFirth’s Modification for Maximum Likelihood EstimationRobust Sandwich Variance EstimateTesting the Global Null HypothesisType 3 TestsConfidence Limits for a Hazard RatioUsing the TEST Statement to Test Linear HypothesesAnalysis of Multivariate Failure Time DataModel Fit StatisticsResidualsDiagnostics Based on Weighted ResidualsInfluence of Observations on Overall Fit of the ModelSurvivor Function EstimatorsEffect Selection MethodsAssessment of the Proportional Hazards ModelThe Penalized Partial Likelihood Approach for Fitting Frailty ModelsSpecifics for Bayesian AnalysisComputational ResourcesInput and Output Data SetsDisplayed OutputODS Table NamesODS Graphics -
Examples
 Stepwise RegressionBest Subset SelectionModeling with Categorical PredictorsFirth’s Correction for Monotone LikelihoodConditional Logistic Regression for m:n MatchingModel Using Time-Dependent Explanatory VariablesTime-Dependent Repeated Measurements of a CovariateSurvival CurvesAnalysis of ResidualsAnalysis of Recurrent Events DataAnalysis of Clustered DataModel Assessment Using Cumulative Sums of Martingale ResidualsBayesian Analysis of the Cox ModelBayesian Analysis of Piecewise Exponential Model
Stepwise RegressionBest Subset SelectionModeling with Categorical PredictorsFirth’s Correction for Monotone LikelihoodConditional Logistic Regression for m:n MatchingModel Using Time-Dependent Explanatory VariablesTime-Dependent Repeated Measurements of a CovariateSurvival CurvesAnalysis of ResidualsAnalysis of Recurrent Events DataAnalysis of Clustered DataModel Assessment Using Cumulative Sums of Martingale ResidualsBayesian Analysis of the Cox ModelBayesian Analysis of Piecewise Exponential Model - References
The Penalized Partial Likelihood Approach for Fitting Frailty Models
Let ![]() be the vector of random components for the s clusters.
be the vector of random components for the s clusters.
Gamma Frailty Model
Assume each ![]() has an independent and identically distributed gamma distribution with mean 1 and a common unknown variance
has an independent and identically distributed gamma distribution with mean 1 and a common unknown variance ![]() ; that is,
; that is, ![]() is iid
is iid ![]() . The penalty function is
. The penalty function is
|
|
plus a function of ![]() . The penalized partial log likelihood is given by
. The penalized partial log likelihood is given by
|
|
where ![]() is the log of any of the partial likelihoods in the sections Partial Likelihood Function for the Cox Model and The Multiplicative Hazards Model.
is the log of any of the partial likelihoods in the sections Partial Likelihood Function for the Cox Model and The Multiplicative Hazards Model.
The profile marginal log-likelihood of this shared frailty model (Therneau and Grambsch, 2000, pp. 257–258) is
|
|
where ![]() is the number of events in the ith cluster.
is the number of events in the ith cluster.
The maximization of this approximate likelihood is a doubly iterative process that alternates between the following two steps:
-
For a provisional value of
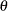 , the best linear unbiased predictors (BLUP) of
, the best linear unbiased predictors (BLUP) of 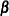 and
and  are computed by maximizing the penalized partial log-likelihood
are computed by maximizing the penalized partial log-likelihood  . The marginal likelihood is evaluated. This constitutes the inner loop.
. The marginal likelihood is evaluated. This constitutes the inner loop.
-
A new value of
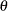 is obtained by the golden section search based on the marginal likelihood of all the previous iterations. This constitutes
the outer loop.
is obtained by the golden section search based on the marginal likelihood of all the previous iterations. This constitutes
the outer loop.
The outer loop is iterated until the bracketing interval of ![]() is small.
is small.
Lognormal Frailty Model
With each ![]() having a zero-mean normal distribution and a common variance
having a zero-mean normal distribution and a common variance ![]() , the penalty function is
, the penalty function is
|
|
plus a function of ![]() . The penalized partial log likelihood is given by
. The penalized partial log likelihood is given by
|
|
where ![]() is the log of any of the partial likelihoods in the sections Partial Likelihood Function for the Cox Model and The Multiplicative Hazards Model.
is the log of any of the partial likelihoods in the sections Partial Likelihood Function for the Cox Model and The Multiplicative Hazards Model.
For a given ![]() , let
, let ![]() be the negative Hessian of the penalized partial log likelihood
be the negative Hessian of the penalized partial log likelihood ![]() ; that is,
; that is,
|
|
where ![]() , and
, and ![]() .
.
The marginal log likelihood of this shared frailty model is
|
|
Using a Laplace approximation to the integral as in Breslow and Clayton (1993), an approximate marginal log likelihood (Ripatti and Palmgren, 2000; Therneau and Grambsch, 2000) is given by
|
|
The maximization of this approximate likelihood is a doubly iterative process that alternates between the following two steps:
-
For a provisional value of
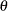 , PROC PHREG computes the best linear unbiased predictors (BLUP) of
, PROC PHREG computes the best linear unbiased predictors (BLUP) of 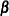 and
and  by maximizing the penalized partial log likelihood
by maximizing the penalized partial log likelihood  . This constitutes the inner loop.
. This constitutes the inner loop.
-
For
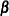 and
and  fixed at the BLUP values, PROC PHREG estimates
fixed at the BLUP values, PROC PHREG estimates 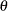 by maximizing the approximate marginal likelihood
by maximizing the approximate marginal likelihood  . This constitutes the outer loop.
. This constitutes the outer loop.
The outer loop is iterated until the difference between two successive estimates of ![]() is small.
is small.
The ML estimate of ![]() is
is
|
|
The variance for ![]() is
is
|
|
The REML estimation of ![]() is obtained by replacing
is obtained by replacing ![]() by
by ![]() .
.
The inverse of the final ![]() matrix is used as the variance estimate of
matrix is used as the variance estimate of ![]() .
.
The final BLUP estimates of the random components ![]() can be displayed by using the SOLUTION option in the RANDOM statement. Also displayed are estimates of the lognormal frailties,
which are the exponentiated estimates of the BLUP estimates.
can be displayed by using the SOLUTION option in the RANDOM statement. Also displayed are estimates of the lognormal frailties,
which are the exponentiated estimates of the BLUP estimates.
Wald-Type Tests for Penalized Models
Let ![]() be the negative Hessian of the partial log likelihood
be the negative Hessian of the partial log likelihood ![]() :
:
|
|
where ![]()
![]() , and
, and ![]() . Write
. Write ![]() . The Wald-type chi-square statistic for testing
. The Wald-type chi-square statistic for testing ![]() is
is
|
|
Let ![]() be the negative Hessian of the penalized partial log likelihood
be the negative Hessian of the penalized partial log likelihood ![]() at the ML estimate
at the ML estimate ![]() ; that is,
; that is, ![]() . Let
. Let ![]() . Gray (1992) recommends the following generalized degrees of freedom for the Wald test:
. Gray (1992) recommends the following generalized degrees of freedom for the Wald test:
|
|
See Therneau and Grambsch (2000, Section 5.8) for a discussion of this Wald-type test.
PROC PHREG uses the label "Adjusted DF" to represent this generalized degrees of freedom in the output.