The NLMIXED Procedure
-
Overview

-
Getting Started

-
Syntax

-
Details
 Modeling Assumptions and NotationIntegral ApproximationsBuilt-in Log-Likelihood FunctionsOptimization AlgorithmsFinite-Difference Approximations of DerivativesHessian ScalingActive Set MethodsLine-Search MethodsRestricting the Step LengthComputational ProblemsCovariance MatrixPredictionComputational ResourcesDisplayed OutputODS Table Names
Modeling Assumptions and NotationIntegral ApproximationsBuilt-in Log-Likelihood FunctionsOptimization AlgorithmsFinite-Difference Approximations of DerivativesHessian ScalingActive Set MethodsLine-Search MethodsRestricting the Step LengthComputational ProblemsCovariance MatrixPredictionComputational ResourcesDisplayed OutputODS Table Names -
Examples

- References
Displayed Output
This section describes the displayed output from PROC NLMIXED. See the section ODS Table Names for details about how this output interfaces with the Output Delivery System.
Specifications
The NLMIXED procedure first displays the “Specifications” table, listing basic information about the nonlinear mixed model that you have specified. It includes the principal variables and estimation methods.
Dimensions
The “Dimensions” table lists counts of important quantities in your nonlinear mixed model, including the number of observations, subjects, parameters, and quadrature points.
Parameters
The “Parameters” table displays the information you provided with the PARMS statement and the value of the negative log-likelihood function evaluated at the starting values.
Starting Gradient and Hessian
The START option in the PROC NLMIXED statement displays the gradient of the negative log-likelihood function at the starting values of the parameters. If you also specify the HESS option, then the starting Hessian is displayed as well.
Iterations
The iteration history consists of one line of output for each iteration in the optimization process. The iteration history is displayed by default because it is important that you check for possible convergence problems. The default iteration history includes the following variables:
-
Iter, the iteration number
-
Calls, the number of function calls
-
NegLogLike, the value of the objective function
-
Diff, the difference between adjacent function values
-
MaxGrad, the maximum of the absolute (projected) gradient components (except NMSIMP)
-
Slope, the slope
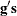 of the search direction
of the search direction  at the current parameter iterate
at the current parameter iterate 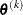 (QUANEW only)
(QUANEW only)
-
Rho, the ratio between the achieved and predicted values of Diff (NRRIDG only)
-
Radius, the radius of the trust region (TRUREG only)
-
StdDev, the standard deviation of the simplex values (NMSIMP only)
-
Delta, the vertex length of the simplex (NMSIMP only)
-
Size, the size of the simplex (NMSIMP only)
For the QUANEW method, the value of Slope should be significantly negative. Otherwise, the line-search algorithm has difficulty
reducing the function value sufficiently. If this difficulty is encountered, an asterisk (*) appears after the iteration number.
If there is a tilde ~after the iteration number, the BFGS update is skipped, and very high values of the Lagrange function are produced. A backslash
(![]() ) after the iteration number indicates that Powell’s correction for the BFGS update is used.
) after the iteration number indicates that Powell’s correction for the BFGS update is used.
For methods using second derivatives, an asterisk (*) after the iteration number means that the computed Hessian approximation was singular and had to be ridged with a positive value.
For the NMSIMP method, only one line is displayed for several internal iterations. This technique skips the output for some iterations because some of the termination tests (StdDev and Size) are rather time-consuming compared to the simplex operations, and they are performed only every five simplex operations.
The ITDETAILS option in the PROC NLMIXED statement provides a more detailed iteration history. Besides listing the current values of the parameters and their gradients, the ITDETAILS option provides the following values in addition to the default output:
-
Restart, the number of iteration restarts
-
Active, the number of active constraints
-
Lambda, the value of the Lagrange multiplier (TRUREG and DBLDOG only)
-
Ridge, the ridge value (NRRIDG only)
-
Alpha, the line-search step size (QUANEW only)
An apostrophe (’) trailing the number of active constraints indicates that at least one of the active constraints was released from the active set due to a significant Lagrange multiplier.
Convergence Status
The “Convergence Status” table contains a status message describing the reason for termination of the optimization. The ODS name of this table is
ConvergenceStatus, and you can query the nonprinting numeric variable Status to check for a successful optimization. This is useful in batch processing, or when processing BY groups, for example, in
simulations. Successful convergence is indicated by Status=0.
Fitting Information
The “Fitting Information” table lists the final minimized value of –2 times the log likelihood as well as the information criteria of Akaike (AIC) and Schwarz (BIC), as well as a finite-sample corrected version of AIC (AICC). The criteria are computed as follows:
|
|
|
|
|
|
|
|
|
where ![]() is the negative of the marginal log-likelihood function,
is the negative of the marginal log-likelihood function, ![]() is the vector of parameter estimates, p is the number of parameters, n is the number of observations, and s is the number of subjects. See Hurvich and Tsai (1989) and Burnham and Anderson (1998) for additional details.
is the vector of parameter estimates, p is the number of parameters, n is the number of observations, and s is the number of subjects. See Hurvich and Tsai (1989) and Burnham and Anderson (1998) for additional details.
Parameter Estimates
The “Parameter Estimates” table lists the estimates of the parameter values after successful convergence of the optimization problem or the final values of the parameters under nonconvergence. If the problem did converge, standard errors are computed from the final Hessian matrix. The ratio of the estimate with its standard error produces a t value, with approximate degrees of freedom computed as the number of subjects minus the number of random effects. A p-value and confidence limits based on this t distribution are also provided. Finally, the gradient of the negative log-likelihood function is displayed for each parameter, and you should verify that they each are sufficiently small for nonconstrained parameters.
Covariance and Correlation Matrices
Following standard maximum likelihood theory (for example, Serfling 1980), the asymptotic variance-covariance matrix of the parameter estimates equals the inverse of the Hessian matrix. You can display this matrix with the COV option in the PROC NLMIXED statement. The corresponding correlation form is available with the CORR option.
Additional Estimates
The “Additional Estimates” table displays the results of all ESTIMATE statements that you specify, with the same columns as the “Parameter Estimates” table. The ECOV and ECORR options in the PROC NLMIXED statement produce tables displaying the approximate covariance and correlation matrices of the additional estimates. They are computed using the delta method (Billingsley, 1986; Cox, 1998). The EDER option in the PROC NLMIXED statement produces a table that displays the derivatives of the additional estimates with respect to the model parameters evaluated at their final estimated values.