The MIXED Procedure
Computational Issues
Computational Method
In addition to numerous matrix-multiplication routines, PROC MIXED frequently uses the sweep operator (Goodnight, 1979) and the Cholesky root (Golub and Van Loan, 1989). The routines perform a modified W transformation (Goodnight and Hemmerle, 1979) for ![]() -side likelihood calculations and a direct method for
-side likelihood calculations and a direct method for ![]() -side likelihood calculations. For the Type 3 F tests, PROC MIXED uses the algorithm described in Chapter 42: The GLM Procedure.
-side likelihood calculations. For the Type 3 F tests, PROC MIXED uses the algorithm described in Chapter 42: The GLM Procedure.
PROC MIXED uses a ridge-stabilized Newton-Raphson algorithm to optimize either a full (ML) or residual (REML) likelihood function. The Newton-Raphson algorithm is preferred to the EM algorithm (Lindstrom and Bates, 1988). PROC MIXED profiles the likelihood with respect to the fixed effects and also with respect to the residual variance whenever it appears reasonable to do so. The residual profiling can be avoided by using the NOPROFILE option of the PROC MIXED statement. PROC MIXED uses the MIVQUE0 method (Rao, 1972; Giesbrecht, 1989) to compute initial values.
The likelihoods that PROC MIXED optimizes are usually well-defined continuous functions with a single optimum. The Newton-Raphson algorithm typically performs well and finds the optimum in a few iterations. It is a quadratically converging algorithm, meaning that the error of the approximation near the optimum is squared at each iteration. The quadratic convergence property is evident when the convergence criterion drops to zero by factors of 10 or more.
Table 59.29: Notation for Order Calculations
|
Symbol |
Number |
|---|---|
|
p |
Columns of |
|
g |
Columns of |
|
N |
Observations |
|
q |
Covariance parameters |
|
t |
Maximum observations per subject |
|
S |
Subjects |
Using the notation from Table 59.29, the following are estimates of the computational speed of the algorithms used in PROC MIXED. For likelihood calculations,
the crossproducts matrix construction is of order ![]() and the sweep operations are of order
and the sweep operations are of order ![]() . The first derivative calculations for parameters in
. The first derivative calculations for parameters in ![]() are of order
are of order ![]() for ML and
for ML and ![]() for REML. If you specify a subject effect in the RANDOM statement and if you are not using the REPEATED statement, then replace g with
for REML. If you specify a subject effect in the RANDOM statement and if you are not using the REPEATED statement, then replace g with ![]() and q with
and q with ![]() in these calculations. The first derivative calculations for parameters in
in these calculations. The first derivative calculations for parameters in ![]() are of order
are of order ![]() for ML and
for ML and ![]() for REML. For the second derivatives, replace q with
for REML. For the second derivatives, replace q with ![]() in the first derivative expressions. When you specify both
in the first derivative expressions. When you specify both ![]() - and
- and ![]() -side parameters (that is, when you use both the RANDOM and REPEATED statements), then additional calculations are required of an order equal to the sum of the orders for
-side parameters (that is, when you use both the RANDOM and REPEATED statements), then additional calculations are required of an order equal to the sum of the orders for ![]() and
and ![]() . Considerable execution times can result in this case.
. Considerable execution times can result in this case.
For further details about the computational techniques used in PROC MIXED, see Wolfinger, Tobias, and Sall (1994).
Parameter Constraints
By default, some covariance parameters are assumed to satisfy certain boundary constraints during the Newton-Raphson algorithm. For example, variance components are constrained to be nonnegative, and autoregressive parameters are constrained to be between –1 and 1. You can remove these constraints with the NOBOUND option in the PARMS statement (or with the NOBOUND option in the PROC MIXED statement), but this can lead to estimates that produce an infinite likelihood. You can also introduce or change boundary constraints with the LOWERB= and UPPERB= options in the PARMS statement.
During the Newton-Raphson algorithm, a parameter might be set equal to one of its boundary constraints for a few iterations and then it might move away from the boundary. You see a missing value in the Criterion column of the “Iteration History” table whenever a boundary constraint is dropped.
For some data sets the final estimate of a parameter might equal one of its boundary constraints. This is usually not a cause for concern, but it might lead you to consider a different model. For instance, a variance component estimate can equal zero; in this case, you might want to drop the corresponding random effect from the model. However, be aware that changing the model in this fashion can affect degrees-of-freedom calculations.
Convergence Problems
For some data sets, the Newton-Raphson algorithm can fail to converge. Nonconvergence can result from a number of causes, including flat or ridged likelihood surfaces and ill-conditioned data.
It is also possible for PROC MIXED to converge to a point that is not the global optimum of the likelihood, although this usually occurs only with the spatial covariance structures.
If you experience convergence problems, the following points might be helpful:
-
One useful tool is the PARMS statement, which lets you input initial values for the covariance parameters and performs a grid search over the likelihood surface.
-
Sometimes the Newton-Raphson algorithm does not perform well when two of the covariance parameters are on a different scale—that is, when they are several orders of magnitude apart. This is because the Hessian matrix is processed jointly for the two parameters, and elements of it corresponding to one of the parameters can become close to internal tolerances in PROC MIXED. In this case, you can improve stability by rescaling the effects in the model so that the covariance parameters are on the same scale.
-
Data that are extremely large or extremely small can adversely affect results because of the internal tolerances in PROC MIXED. Rescaling it can improve stability.
-
For stubborn problems, you might want to specify ODS OUTPUT COVPARMS=data-set-name to output the “Covariance Parameter Estimates” table as a precautionary measure. That way, if the problem does not converge, you can read the final parameter values back into a new run with the PARMSDATA= option in the PARMS statement.
-
Fisher scoring can be more robust than Newton-Raphson with poor MIVQUE(0) starting values. Specifying a SCORING= value of 5 or so might help to recover from poor starting values.
-
Tuning the singularity options SINGULAR=, SINGCHOL=, and SINGRES= in the MODEL statement can improve the stability of the optimization process.
-
Tuning the MAXITER= and MAXFUNC= options in the PROC MIXED statement can save resources. Also, the ITDETAILS option displays the values of all the parameters at each iteration.
-
Using the NOPROFILE and NOBOUND options in the PROC MIXED statement might help convergence, although they can produce unusual results.
-
Although the CONVH convergence criterion usually gives the best results, you might want to try CONVF or CONVG, possibly along with the ABSOLUTE option.
-
If the convergence criterion reaches a relatively small value such as 1E–7 but never gets lower than 1E–8, you might want to specify CONVH=1E–6 in the PROC MIXED statement to get results; however, interpret the results with caution.
-
An infinite likelihood during the iteration process means that the Newton-Raphson algorithm has stepped into a region where either the
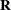 or
or 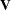 matrix is nonpositive definite. This is usually no cause for concern as long as iterations continue. If PROC MIXED stops
because of an infinite likelihood, recheck your model to make sure that no observations from the same subject are producing
identical rows in
matrix is nonpositive definite. This is usually no cause for concern as long as iterations continue. If PROC MIXED stops
because of an infinite likelihood, recheck your model to make sure that no observations from the same subject are producing
identical rows in 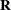 or
or 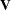 and that you have enough data to estimate the particular covariance structure you have selected. Any time that the final
estimated likelihood is infinite, subsequent results should be interpreted with caution.
and that you have enough data to estimate the particular covariance structure you have selected. Any time that the final
estimated likelihood is infinite, subsequent results should be interpreted with caution.
-
A nonpositive definite Hessian matrix can indicate a surface saddlepoint or linear dependencies among the parameters.
-
A warning message about the singularities of
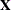 changing indicates that there is some linear dependency in the estimate of
changing indicates that there is some linear dependency in the estimate of 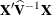 that is not found in
that is not found in 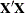 . This can adversely affect the likelihood calculations and optimization process. If you encounter this problem, make sure
that your model specification is reasonable and that you have enough data to estimate the particular covariance structure
you have selected. Rearranging effects in the MODEL statement so that the most significant ones are first can help, because PROC MIXED sweeps the estimate of
. This can adversely affect the likelihood calculations and optimization process. If you encounter this problem, make sure
that your model specification is reasonable and that you have enough data to estimate the particular covariance structure
you have selected. Rearranging effects in the MODEL statement so that the most significant ones are first can help, because PROC MIXED sweeps the estimate of 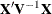 in the order of the MODEL effects and the sweep is more stable if larger pivots are dealt with first. If this does not help,
specifying starting values with the PARMS statement can place the optimization on a different and possibly more stable path.
in the order of the MODEL effects and the sweep is more stable if larger pivots are dealt with first. If this does not help,
specifying starting values with the PARMS statement can place the optimization on a different and possibly more stable path.
-
Lack of convergence can indicate model misspecification or a violation of the normality assumption.
Memory
Let p be the number of columns in ![]() , and let g be the number of columns in
, and let g be the number of columns in ![]() . For large models, most of the memory resources are required for holding symmetric matrices of order p, g, and
. For large models, most of the memory resources are required for holding symmetric matrices of order p, g, and ![]() . The approximate memory requirement in bytes is
. The approximate memory requirement in bytes is
|
|
If you have a large model that exceeds the memory capacity of your computer, see the suggestions listed under “Computing Time.”
Computing Time
PROC MIXED is computationally intensive, and execution times can be long. In addition to the CPU time used in collecting sums and crossproducts and in solving the mixed model equations (as in PROC GLM), considerable CPU time is often required to compute the likelihood function and its derivatives. These latter computations are performed for every Newton-Raphson iteration.
If you have a model that takes too long to run, the following suggestions can be helpful:
-
Examine the “Model Information” table to find out the number of columns in the
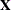 and
and 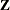 matrices. A large number of columns in either matrix can greatly increase computing time. You might want to eliminate some
higher-order effects if they are too large.
matrices. A large number of columns in either matrix can greatly increase computing time. You might want to eliminate some
higher-order effects if they are too large.
-
If you have a
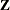 matrix with a lot of columns, use the DDFM=BW option in the MODEL statement to eliminate the time required for the containment method.
matrix with a lot of columns, use the DDFM=BW option in the MODEL statement to eliminate the time required for the containment method.
-
If possible, “factor out” a common effect from the effects in the RANDOM statement and make it the SUBJECT= effect. This creates a block-diagonal
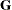 matrix and can often speed calculations.
matrix and can often speed calculations.
-
If possible, use the same or nested SUBJECT= effects in all RANDOM and REPEATED statements.
-
If your data set is very large, you might want to analyze it in pieces. The BY statement can help implement this strategy.
-
In general, specify random effects with a lot of levels in the REPEATED statement and those with a few levels in the RANDOM statement.
-
The METHOD=MIVQUE0 option runs faster than either the METHOD=REML or METHOD=ML option because it is noniterative.
-
You can specify known values for the covariance parameters by using the HOLD= or NOITER option in the PARMS statement or the GDATA= option in the RANDOM statement. This eliminates the need for iteration.
-
The LOGNOTE option in the PROC MIXED statement writes periodic messages to the SAS log concerning the status of the calculations. It can help you diagnose where the slowdown is occurring.
