Bayesian Inference
Bayesian inference about ![]() is primarily based on the posterior distribution of
is primarily based on the posterior distribution of ![]() . There are various ways in which you can summarize this distribution. For example, you can report your findings through point
estimates. You can also use the posterior distribution to construct hypothesis tests or probability statements.
. There are various ways in which you can summarize this distribution. For example, you can report your findings through point
estimates. You can also use the posterior distribution to construct hypothesis tests or probability statements.
Point Estimation and Estimation Error
Classical methods often report the maximum likelihood estimator (MLE) or the method of moments estimator (MOME) of a parameter. In contrast, Bayesian approaches often use the posterior mean. The definition of the posterior mean is given by
|
|
Other commonly used posterior estimators include the posterior median, defined as
|
|
and the posterior mode, defined as the value of ![]() that maximizes
that maximizes ![]() .
.
The variance of the posterior density (simply referred to as the posterior variance) describes the uncertainty in the parameter, which is a random variable in the Bayesian paradigm. A Bayesian analysis typically uses the posterior variance, or the posterior standard deviation, to characterize the dispersion of the parameter. In multidimensional models, covariance or correlation matrices are used.
If you know the distributional form of the posterior density of interest, you can report the exact posterior point estimates. When models become too difficult to analyze analytically, you have to use simulation algorithms, such as the Markov chain Monte Carlo (MCMC) method to obtain posterior estimates (see the section Markov Chain Monte Carlo Method). All of the Bayesian procedures rely on MCMC to obtain all posterior estimates. Using only a finite number of samples, simulations introduce an additional level of uncertainty to the accuracy of the estimates. Monte Carlo standard error (MCSE), which is the standard error of the posterior mean estimate, measures the simulation accuracy. See the section Standard Error of the Mean Estimate for more information.
The posterior standard deviation and the MCSE are two completely different concepts: the posterior standard deviation describes the uncertainty in the parameter, while the MCSE describes only the uncertainty in the parameter estimate as a result of MCMC simulation. The posterior standard deviation is a function of the sample size in the data set, and the MCSE is a function of the number of iterations in the simulation.
Hypothesis Testing
Suppose you have the following null and alternative hypotheses: ![]() is
is ![]() and
and ![]() is
is ![]() , where
, where ![]() is a subset of the parameter space and
is a subset of the parameter space and ![]() is its complement. Using the posterior distribution
is its complement. Using the posterior distribution ![]() , you can compute the posterior probabilities
, you can compute the posterior probabilities ![]() and
and ![]() , or the probabilities that
, or the probabilities that ![]() and
and ![]() are true, respectively. One way to perform a Bayesian hypothesis test is to accept the null hypothesis if
are true, respectively. One way to perform a Bayesian hypothesis test is to accept the null hypothesis if ![]() and vice versa, or to accept the null hypothesis if
and vice versa, or to accept the null hypothesis if ![]() is greater than a predefined threshold, such as 0.75, to guard against falsely accepted null distribution.
is greater than a predefined threshold, such as 0.75, to guard against falsely accepted null distribution.
It is more difficult to carry out a point null hypothesis test in a Bayesian analysis. A point null hypothesis is a test of
![]() versus
versus ![]() . If the prior distribution
. If the prior distribution ![]() is a continuous density, then the posterior probability of the null hypothesis being true is 0, and there is no point in
carrying out the test. One alternative is to restate the null to be a small interval hypothesis:
is a continuous density, then the posterior probability of the null hypothesis being true is 0, and there is no point in
carrying out the test. One alternative is to restate the null to be a small interval hypothesis: ![]() , where a is a very small constant. The Bayesian paradigm can deal with an interval hypothesis more easily. Another approach is to
give a mixture prior distribution to
, where a is a very small constant. The Bayesian paradigm can deal with an interval hypothesis more easily. Another approach is to
give a mixture prior distribution to ![]() with a positive probability of
with a positive probability of ![]() on
on ![]() and the density
and the density ![]() on
on ![]() . This prior ensures a nonzero posterior probability on
. This prior ensures a nonzero posterior probability on ![]() , and you can then make realistic probabilistic comparisons. For more detailed treatment of Bayesian hypothesis testing, see
Berger (1985).
, and you can then make realistic probabilistic comparisons. For more detailed treatment of Bayesian hypothesis testing, see
Berger (1985).
Interval Estimation
The Bayesian set estimates are called credible sets, which is also known as credible intervals. This is analogous to the concept of confidence intervals used in classical statistics. Given a posterior distribution ![]() , A is a credible set for
, A is a credible set for ![]() if
if
|
|
For example, you can construct a 95% credible set for ![]() by finding an interval, A, over which
by finding an interval, A, over which ![]() .
.
You can construct credible sets that have equal tails. A ![]() equal-tail interval corresponds to the
equal-tail interval corresponds to the ![]() and
and ![]() percentiles of the posterior distribution. Some statisticians prefer this interval because it is invariant under transformations. Another frequently used Bayesian credible
set is called the highest posterior density (HPD) interval.
percentiles of the posterior distribution. Some statisticians prefer this interval because it is invariant under transformations. Another frequently used Bayesian credible
set is called the highest posterior density (HPD) interval.
A ![]() HPD interval is a region that satisfies the following two conditions:
HPD interval is a region that satisfies the following two conditions:
-
The posterior probability of that region is
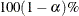 .
.
-
The minimum density of any point within that region is equal to or larger than the density of any point outside that region.
The HPD is an interval in which most of the distribution lies. Some statisticians prefer this interval because it is the smallest interval.
One major distinction between Bayesian and classical sets is their interpretation. The Bayesian probability reflects a person’s
subjective beliefs. Following this approach, a statistician can make the claim that ![]() is inside a credible interval with measurable probability. This property is appealing because it enables you to make a direct
probability statement about parameters. Many people find this concept to be a more natural way of understanding a probability
interval, which is also easier to explain to nonstatisticians. A confidence interval, on the other hand, enables you to make
a claim that the interval covers the true parameter. The interpretation reflects the uncertainty in the sampling procedure;
a confidence interval of
is inside a credible interval with measurable probability. This property is appealing because it enables you to make a direct
probability statement about parameters. Many people find this concept to be a more natural way of understanding a probability
interval, which is also easier to explain to nonstatisticians. A confidence interval, on the other hand, enables you to make
a claim that the interval covers the true parameter. The interpretation reflects the uncertainty in the sampling procedure;
a confidence interval of ![]() asserts that, in the long run,
asserts that, in the long run, ![]() of the realized confidence intervals cover the true parameter.
of the realized confidence intervals cover the true parameter.