The GLM Procedure
-
Overview

-
Getting Started

-
Syntax

-
Details
 Statistical Assumptions for Using PROC GLMSpecification of EffectsUsing PROC GLM InteractivelyParameterization of PROC GLM ModelsHypothesis Testing in PROC GLMEffect Size Measures for F Tests in GLMAbsorptionSpecification of ESTIMATE ExpressionsComparing GroupsMultivariate Analysis of VarianceRepeated Measures Analysis of VarianceRandom-Effects AnalysisMissing ValuesComputational ResourcesComputational MethodOutput Data SetsDisplayed OutputODS Table NamesODS Graphics
Statistical Assumptions for Using PROC GLMSpecification of EffectsUsing PROC GLM InteractivelyParameterization of PROC GLM ModelsHypothesis Testing in PROC GLMEffect Size Measures for F Tests in GLMAbsorptionSpecification of ESTIMATE ExpressionsComparing GroupsMultivariate Analysis of VarianceRepeated Measures Analysis of VarianceRandom-Effects AnalysisMissing ValuesComputational ResourcesComputational MethodOutput Data SetsDisplayed OutputODS Table NamesODS Graphics -
Examples
 Randomized Complete Blocks with Means Comparisons and ContrastsRegression with Mileage DataUnbalanced ANOVA for Two-Way Design with InteractionAnalysis of CovarianceThree-Way Analysis of Variance with ContrastsMultivariate Analysis of VarianceRepeated Measures Analysis of VarianceMixed Model Analysis of Variance with the RANDOM StatementAnalyzing a Doubly Multivariate Repeated Measures DesignTesting for Equal Group VariancesAnalysis of a Screening Design
Randomized Complete Blocks with Means Comparisons and ContrastsRegression with Mileage DataUnbalanced ANOVA for Two-Way Design with InteractionAnalysis of CovarianceThree-Way Analysis of Variance with ContrastsMultivariate Analysis of VarianceRepeated Measures Analysis of VarianceMixed Model Analysis of Variance with the RANDOM StatementAnalyzing a Doubly Multivariate Repeated Measures DesignTesting for Equal Group VariancesAnalysis of a Screening Design - References
Repeated Measures Analysis of Variance
When several measurements are taken on the same experimental unit (person, plant, machine, and so on), the measurements tend to be correlated with each other. When the measurements represent qualitatively different things, such as weight, length, and width, this correlation is best taken into account by use of multivariate methods, such as multivariate analysis of variance. When the measurements can be thought of as responses to levels of an experimental factor of interest, such as time, treatment, or dose, the correlation can be taken into account by performing a repeated measures analysis of variance.
PROC GLM provides both univariate and multivariate tests for repeated measures for one response. For an overall reference on univariate repeated measures, see Winer (1971). The multivariate approach is covered in Cole and Grizzle (1966). For a discussion of the relative merits of the two approaches, see LaTour and Miniard (1983).
Another approach to analysis of repeated measures is via general mixed models. This approach can handle balanced as well as unbalanced or missing within-subject data, and it offers more options for modeling the within-subject covariance. The main drawback of the mixed models approach is that it generally requires iteration and, thus, might be less computationally efficient. For further details on this approach, see Chapter 59: The MIXED Procedure, and Wolfinger and Chang (1995).
Organization of Data for Repeated Measure Analysis
In order to deal efficiently with the correlation of repeated measures, the GLM procedure uses the multivariate method of
specifying the model, even if only a univariate analysis is desired. In some cases, data might already be entered in the univariate
mode, with each repeated measure listed as a separate observation along with a variable that represents the experimental unit
(subject) on which measurement is taken. Consider the following data set Old:
data Old; input Subject Group Time y; datalines; 1 1 1 15 1 1 2 19 1 1 3 25 2 1 1 21 2 1 2 18 2 1 3 17 1 2 1 14 1 2 2 12 1 2 3 16 2 2 1 11 2 2 2 20 2 2 3 21 ... more lines ... 10 3 1 14 10 3 2 18 10 3 3 16 ;
There are three observations for each subject, corresponding to measurements taken at times 1, 2, and 3. These data could be analyzed using the following statements:
proc glm data=Old; class Group Subject Time; model y=Group Subject(Group) Time Group*Time; test h=Group e=Subject(Group); run;
However, this analysis assumes subjects’ measurements are uncorrelated across time. A repeated measures analysis does not
make this assumption. It uses the following data set New:
data New; input Group y1 y2 y3; datalines; 1 15 19 25 1 21 18 17 2 14 12 16 2 11 20 21 2 24 15 12 ... more lines ... 3 14 18 16 ;
In the data set New, the three measurements for a subject are all in one observation. For example, the measurements for subject 1 for times 1,
2, and 3 are 15, 19, and 25, respectively. For these data, the statements for a repeated measures analysis (assuming default
options) are
proc glm data=New; class Group; model y1-y3 = Group / nouni; repeated Time; run;
To convert the univariate form of repeated measures data to the multivariate form, you can use a program like the following:
proc sort data=Old;
by Group Subject;
run;
data New(keep=y1-y3 Group);
array yy(3) y1-y3;
do Time = 1 to 3;
set Old;
by Group Subject;
yy(Time) = y;
if last.Subject then return;
end;
run;
Alternatively, you could use PROC TRANSPOSE to achieve the same results with a program like this one:
proc sort data=Old; by Group Subject; run; proc transpose out=New(rename=(_1=y1 _2=y2 _3=y3)); by Group Subject; id Time; run;
See the discussions in SAS Language Reference: Concepts for more information about rearrangement of data sets.
Hypothesis Testing in Repeated Measures Analysis
In repeated measures analysis of variance, the effects of interest are as follows:
-
between-subject effects (such as GROUP in the previous example)
-
within-subject effects (such as TIME in the previous example)
-
interactions between the two types of effects (such as GROUP*TIME in the previous example)
Repeated measures analyses are distinguished from MANOVA because of interest in testing hypotheses about the within-subject effects and the within-subject-by-between-subject interactions.
For tests that involve only between-subjects effects, both the multivariate and univariate approaches give rise to the same tests. These tests are provided for all effects in the MODEL statement, as well as for any CONTRASTs specified. The ANOVA table for these tests is labeled “Tests of Hypotheses for Between Subjects Effects” in the PROC GLM results. These tests are constructed by first adding together the dependent variables in the model. Then an analysis of variance is performed on the sum divided by the square root of the number of dependent variables. For example, the statements
model y1-y3=group; repeated time;
give a one-way analysis of variance that uses ![]() as the dependent variable for performing tests of hypothesis on the between-subject effect GROUP. Tests for between-subject
effects are equivalent to tests of the hypothesis
as the dependent variable for performing tests of hypothesis on the between-subject effect GROUP. Tests for between-subject
effects are equivalent to tests of the hypothesis ![]() , where
, where ![]() is simply a vector of 1s.
is simply a vector of 1s.
For within-subject effects and for within-subject-by-between-subject interaction effects, the univariate and multivariate approaches yield different tests. These tests are provided for the within-subject effects and for the interactions between these effects and the other effects in the MODEL statement, as well as for any CONTRASTs specified. The univariate tests are displayed in a table labeled “Univariate Tests of Hypotheses for Within Subject Effects.” Results for multivariate tests are displayed in a table labeled “Repeated Measures Analysis of Variance.”
The multivariate tests provided for within-subjects effects and interactions involving these effects are Wilks’ lambda, Pillai’s trace, Hotelling-Lawley trace, and Roy’s greatest root. For further details on these four statistics, see the “Multivariate Tests” section in Chapter 4: Introduction to Regression Procedures. As an example, the statements
model y1-y3=group; repeated time;
produce multivariate tests for the within-subject effect TIME and the interaction TIME*GROUP.
The multivariate tests for within-subject effects are produced by testing the hypothesis ![]() , where the
, where the ![]() matrix is the usual matrix corresponding to the Type I, Type II, Type III, or Type IV hypotheses test, and the
matrix is the usual matrix corresponding to the Type I, Type II, Type III, or Type IV hypotheses test, and the ![]() matrix is one of several matrices depending on the transformation that you specify in the REPEATED statement. These multivariate tests require that the column rank of
matrix is one of several matrices depending on the transformation that you specify in the REPEATED statement. These multivariate tests require that the column rank of ![]() be less than or equal to the number of error degrees of freedom. Besides that, the only assumption required for valid tests
is that the dependent variables in the model have a multivariate normal distribution with a common covariance matrix across
the between-subject effects.
be less than or equal to the number of error degrees of freedom. Besides that, the only assumption required for valid tests
is that the dependent variables in the model have a multivariate normal distribution with a common covariance matrix across
the between-subject effects.
The univariate tests for within-subject effects and interactions involving these effects require some assumptions for the probabilities provided by the ordinary F tests to be correct. Specifically, these tests require certain patterns of covariance matrices, known as Type H covariances (Huynh and Feldt, 1970). Data with these patterns in the covariance matrices are said to satisfy the Huynh-Feldt condition. You can test this assumption (and the Huynh-Feldt condition) by applying a sphericity test (Anderson, 1958) to any set of variables defined by an orthogonal contrast transformation. Such a set of variables is known as a set of orthogonal components. When you use the PRINTE option in the REPEATED statement, this sphericity test is applied both to the transformed variables defined by the REPEATED statement and to a set of orthogonal components if the specified transformation is not orthogonal. It is the test applied to the orthogonal components that is important in determining whether your data have a Type H covariance structure. When there are only two levels of the within-subject effect, there is only one transformed variable, and a sphericity test is not needed. The sphericity test is labeled “Test for Sphericity” in the output.
If your data satisfy the preceding assumptions, use the usual F tests to test univariate hypotheses for the within-subject effects and associated interactions.
If your data do not satisfy the assumption of Type H covariance, an adjustment to numerator and denominator degrees of freedom
can be used. Several such adjustments, based on a degrees-of-freedom adjustment factor known as ![]() (epsilon) (Box, 1954), are provided in PROC GLM. All these adjustments estimate
(epsilon) (Box, 1954), are provided in PROC GLM. All these adjustments estimate ![]() and then multiply the numerator and denominator degrees of freedom by this estimate before determining significance levels
for the F tests. Significance levels associated with the adjusted tests are labeled “Adj Pr > F” in the output. Two such adjustments are displayed. One is the maximum likelihood estimate of Box’s
and then multiply the numerator and denominator degrees of freedom by this estimate before determining significance levels
for the F tests. Significance levels associated with the adjusted tests are labeled “Adj Pr > F” in the output. Two such adjustments are displayed. One is the maximum likelihood estimate of Box’s ![]() factor, which is known to be conservative, possibly very much so. The other adjustment is intended to be unbiased although possibly
at the cost of being liberal. The first adjustment is labeled as the “Greenhouse-Geisser Epsilon.” It has the form
factor, which is known to be conservative, possibly very much so. The other adjustment is intended to be unbiased although possibly
at the cost of being liberal. The first adjustment is labeled as the “Greenhouse-Geisser Epsilon.” It has the form
|
|
|
|
where ![]() is the error matrix for the corresponding multivariate test and b is the degrees of freedom for the hypothesis being tested.
is the error matrix for the corresponding multivariate test and b is the degrees of freedom for the hypothesis being tested. ![]() was initially proposed for use in data analysis by Greenhouse and Geisser (1959). Significance levels associated with F tests thus adjusted are labeled “G-G” in the output.
was initially proposed for use in data analysis by Greenhouse and Geisser (1959). Significance levels associated with F tests thus adjusted are labeled “G-G” in the output.
Huynh and Feldt (1976) showed that ![]() tends to be biased downward (that is, conservative), especially for small samples. Alternative estimates have been proposed
to overcome this conservative bias, and there are several options for which estimate to display along with
tends to be biased downward (that is, conservative), especially for small samples. Alternative estimates have been proposed
to overcome this conservative bias, and there are several options for which estimate to display along with ![]() .
.
-
Huynh and Feldt (1976) proposed an estimate of Box’s epsilon, constructed using estimators of its numerator and denominator that are intended to be unbiased. The Huynh-Feldt epsilon has the form of a modification of the Greenhouse-Geisser epsilon,

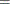

where n is the number of subjects and DFE is the degrees of freedom for error. The numerator of this estimate is precisely unbiased only when there are no between-subject effects, but
 is still often employed even with nontrivial between-subject models; it was the only unbiased epsilon alternative in SAS/STAT
releases before SAS/STAT 9.22. The Huynh-Feldt epsilon is no longer the default, but you can request it and its corresponding
F test by using the UEPSDEF=HF option in the REPEATED statement. The estimate is labeled “Huynh-Feldt Epsilon” in the PROC GLM output, and the significance levels associated with adjusted F tests are labeled “H-F.”
is still often employed even with nontrivial between-subject models; it was the only unbiased epsilon alternative in SAS/STAT
releases before SAS/STAT 9.22. The Huynh-Feldt epsilon is no longer the default, but you can request it and its corresponding
F test by using the UEPSDEF=HF option in the REPEATED statement. The estimate is labeled “Huynh-Feldt Epsilon” in the PROC GLM output, and the significance levels associated with adjusted F tests are labeled “H-F.” -
Lecoutre (1991) gave the unbiased form of the numerator of Box’s epsilon when there is one between-subject effect. The correct form of Huynh and Feldt’s idea in this case is

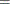

More recently, Gribbin (2007) showed that
 applies to general between-subject models, and Chi et al. (2012) showed that it extends even to situations where the number of error degrees of freedom is less than the column rank of the
within-subject contrast matrix. Thus, the Lecoutre correction of the Huynh-Feldt epsilon is displayed by default along with
the Greenhouse-Geisser epsilon; you can also explicitly request it by using the UEPSDEF=HFL option in the REPEATED statement. The estimate is labeled “Huynh-Feldt-Lecoutre Epsilon” in the PROC GLM output, and the significance levels associated with adjusted F tests are labeled “H-F-L.”
applies to general between-subject models, and Chi et al. (2012) showed that it extends even to situations where the number of error degrees of freedom is less than the column rank of the
within-subject contrast matrix. Thus, the Lecoutre correction of the Huynh-Feldt epsilon is displayed by default along with
the Greenhouse-Geisser epsilon; you can also explicitly request it by using the UEPSDEF=HFL option in the REPEATED statement. The estimate is labeled “Huynh-Feldt-Lecoutre Epsilon” in the PROC GLM output, and the significance levels associated with adjusted F tests are labeled “H-F-L.”
-
Finally, Chi et al. (2012) suggest that Box’s epsilon might be better estimated by replacing the reciprocal of an unbiased form of the denominator with an approximately unbiased form of the reciprocal itself. The resulting estimator can be written as a multiple of the corrected Huynh-Feldt epsilon
 ,
,

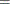

where
 . Simulations indicate that
. Simulations indicate that  does a good job of providing accurate p-values without being either too conservative or too liberal. Over a wide range of cases, it is never much worse than any
other alternative epsilon and often much better. You can request that the Chi-Muller epsilon estimate and its corresponding
F test be displayed by using the UEPSDEF=CM option in the REPEATED statement. The estimate is labeled “Chi-Muller Epsilon” in the PROC GLM output, and the significance levels associated with adjusted F tests are labeled “C-M.”
does a good job of providing accurate p-values without being either too conservative or too liberal. Over a wide range of cases, it is never much worse than any
other alternative epsilon and often much better. You can request that the Chi-Muller epsilon estimate and its corresponding
F test be displayed by using the UEPSDEF=CM option in the REPEATED statement. The estimate is labeled “Chi-Muller Epsilon” in the PROC GLM output, and the significance levels associated with adjusted F tests are labeled “C-M.”
Although ![]() must be in the range of 0 to 1, the three approximately unbiased estimators can be outside this range. When any of these
estimators is greater than 1, a value of 1 is used in all calculations for probabilities—in other words, the probabilities
are not adjusted. Additionally, if
must be in the range of 0 to 1, the three approximately unbiased estimators can be outside this range. When any of these
estimators is greater than 1, a value of 1 is used in all calculations for probabilities—in other words, the probabilities
are not adjusted. Additionally, if ![]() , then the degrees of freedom are adjusted by
, then the degrees of freedom are adjusted by ![]() instead of
instead of ![]() .
.
In summary, if your data do not meet the assumptions, use adjusted F tests. However, when you strongly suspect that your data might not have Type H covariance, all these univariate tests should be interpreted cautiously. In such cases, you should consider using the multivariate tests instead.
The univariate sums of squares for hypotheses involving within-subject effects can be easily calculated from the ![]() and
and ![]() matrices corresponding to the multivariate tests described in the section Multivariate Analysis of Variance. If the
matrices corresponding to the multivariate tests described in the section Multivariate Analysis of Variance. If the ![]() matrix is orthogonal, the univariate sums of squares is calculated as the trace (sum of diagonal elements) of the appropriate
matrix is orthogonal, the univariate sums of squares is calculated as the trace (sum of diagonal elements) of the appropriate
![]() matrix; if it is not orthogonal, PROC GLM calculates the trace of the
matrix; if it is not orthogonal, PROC GLM calculates the trace of the ![]() matrix that results from an orthogonal
matrix that results from an orthogonal ![]() matrix transformation. The appropriate error term for the univariate F tests is constructed in a similar way from the error SSCP matrix and is labeled Error(factorname), where factorname indicates the
matrix transformation. The appropriate error term for the univariate F tests is constructed in a similar way from the error SSCP matrix and is labeled Error(factorname), where factorname indicates the ![]() matrix that is used in the transformation.
matrix that is used in the transformation.
When the design specifies more than one repeated measures factor, PROC GLM computes the ![]() matrix for a given effect as the direct (Kronecker) product of the
matrix for a given effect as the direct (Kronecker) product of the ![]() matrices defined by the REPEATED statement if the factor is involved in the effect or as a vector of 1s if the factor is not involved. The test for the main
effect of a repeated measures factor is constructed using an
matrices defined by the REPEATED statement if the factor is involved in the effect or as a vector of 1s if the factor is not involved. The test for the main
effect of a repeated measures factor is constructed using an ![]() matrix that corresponds to a test that the mean of the observation is zero. Thus, the main effect test for repeated measures
is a test that the means of the variables defined by the
matrix that corresponds to a test that the mean of the observation is zero. Thus, the main effect test for repeated measures
is a test that the means of the variables defined by the ![]() matrix are all equal to zero, while interactions involving repeated measures effects are tests that the between-subjects
factors involved in the interaction have no effect on the means of the transformed variables defined by the
matrix are all equal to zero, while interactions involving repeated measures effects are tests that the between-subjects
factors involved in the interaction have no effect on the means of the transformed variables defined by the ![]() matrix. In addition, you can specify other
matrix. In addition, you can specify other ![]() matrices to test hypotheses of interest by using the CONTRAST statement, since hypotheses defined by CONTRAST statements are also tested in the REPEATED analysis. To see which combinations of the original variables the transformed variables represent, you can specify the PRINTM option in the REPEATED statement. This option displays the transpose of
matrices to test hypotheses of interest by using the CONTRAST statement, since hypotheses defined by CONTRAST statements are also tested in the REPEATED analysis. To see which combinations of the original variables the transformed variables represent, you can specify the PRINTM option in the REPEATED statement. This option displays the transpose of ![]() , which is labeled as M in the PROC GLM results. The tests produced are the same for any choice of transformation
, which is labeled as M in the PROC GLM results. The tests produced are the same for any choice of transformation ![]() matrix specified in the REPEATED statement; however, depending on the nature of the repeated measurements being studied, a particular choice of transformation
matrix, coupled with the CANONICAL or SUMMARY option, can provide additional insight into the data being studied.
matrix specified in the REPEATED statement; however, depending on the nature of the repeated measurements being studied, a particular choice of transformation
matrix, coupled with the CANONICAL or SUMMARY option, can provide additional insight into the data being studied.
Transformations Used in Repeated Measures Analysis of Variance
As mentioned in the specifications of the REPEATED statement, several different ![]() matrices can be generated automatically, based on the transformation that you specify in the REPEATED statement. Remember that both the univariate and multivariate tests that PROC GLM performs are unaffected by the choice of
transformation; the choice of transformation is important only when you are trying to study the nature of a repeated measures
effect, particularly with the CANONICAL and SUMMARY options. If one of these matrices does not meet your needs for a particular analysis, you might want to use the M= option in the MANOVA statement to perform the tests of interest.
matrices can be generated automatically, based on the transformation that you specify in the REPEATED statement. Remember that both the univariate and multivariate tests that PROC GLM performs are unaffected by the choice of
transformation; the choice of transformation is important only when you are trying to study the nature of a repeated measures
effect, particularly with the CANONICAL and SUMMARY options. If one of these matrices does not meet your needs for a particular analysis, you might want to use the M= option in the MANOVA statement to perform the tests of interest.
The following sections describe the transformations available in the REPEATED statement, provide an example of the ![]() matrix that is produced, and give guidelines for the use of the transformation. As in the PROC GLM output, the displayed
matrix is labeled M. This is the
matrix that is produced, and give guidelines for the use of the transformation. As in the PROC GLM output, the displayed
matrix is labeled M. This is the ![]() matrix.
matrix.
CONTRAST Transformation
This is the default transformation used by the REPEATED statement. It is useful when one level of the repeated measures effect can be thought of as a control level against which the others are compared. For example, if five drugs are administered to each of several animals and the first drug is a control or placebo, the statements
proc glm; model d1-d5= / nouni; repeated drug 5 contrast(1) / summary printm; run;
produce the following ![]() matrix:
matrix:
![\[ \mb {M} = \left[ \begin{array}{rrrrr} -1 & 1 & 0 & 0 & 0 \\ -1 & 0 & 1 & 0 & 0 \\ -1 & 0 & 0 & 1 & 0 \\ -1 & 0 & 0 & 0 & 1 \\ \end{array} \right] \]](images/statug_glm0414.png) |
When you examine the analysis of variance tables produced by the SUMMARY option, you can tell which of the drugs differed significantly from the placebo.
POLYNOMIAL Transformation
This transformation is useful when the levels of the repeated measure represent quantitative values of a treatment, such as
dose or time. If the levels are unequally spaced, level values can be specified in parentheses after the number of levels in the REPEATED statement. For example, if five levels of a drug corresponding to 1, 2, 5, 10, and 20 milligrams are administered to different
treatment groups, represented by the variable group, the statements
proc glm; class group; model r1-r5=group / nouni; repeated dose 5 (1 2 5 10 20) polynomial / summary printm; run;
produce the following ![]() matrix:
matrix:
![\[ \mb {M} = \left[ \begin{array}{rrrrr} -0.4250 & -0.3606 & -0.1674 & 0.1545 & 0.7984 \\ 0.4349 & 0.2073 & -0.3252 & -0.7116 & 0.3946 \\ -0.4331 & 0.1366 & 0.7253 & -0.5108 & 0.0821 \\ 0.4926 & -0.7800 & 0.3743 & -0.0936 & 0.0066 \\ \end{array} \right] \]](images/statug_glm0415.png) |
The SUMMARY option in this example provides univariate ANOVAs for the variables defined by the rows of this ![]() matrix. In this case, they represent the linear, quadratic, cubic, and quartic trends for dose and are labeled dose_1, dose_2,
dose_3, and dose_4, respectively.
matrix. In this case, they represent the linear, quadratic, cubic, and quartic trends for dose and are labeled dose_1, dose_2,
dose_3, and dose_4, respectively.
HELMERT Transformation
Since the Helmert transformation compares a level of a repeated measure to the mean of subsequent levels, it is useful when interest lies in the point at which responses cease to change. For example, if four levels of a repeated measures factor represent responses to treatments administered over time to males and females, the statements
proc glm; class sex; model resp1-resp4=sex / nouni; repeated trtmnt 4 helmert / canon printm; run;
produce the following ![]() matrix:
matrix:
![\[ \mb {M} = \left[ \begin{array}{rccc} 1 & -0.33333 & -0.33333 & -0.33333 \\ 0 & 1 & -0.50000 & -0.50000 \\ 0 & 0 & 1 & -1 \\ \end{array} \right] \]](images/statug_glm0416.png) |
MEAN Transformation
This transformation can be useful in the same types of situations in which the CONTRAST transformation is useful. If you substitute the following statement for the REPEATED statement shown in the CONTRAST Transformation section,
repeated drug 5 mean / printm;
the following ![]() matrix is produced:
matrix is produced:
![\[ \mb {M} = \left[ \begin{array}{ccccc} 1 & -0.25 & -0.25 & -0.25 & -0.25 \\ -0.25 & 1 & -0.25 & -0.25 & -0.25 \\ -0.25 & -0.25 & 1 & -0.25 & -0.25 \\ -0.25 & -0.25 & -0.25 & 1 & -0.25 \\ \end{array} \right] \]](images/statug_glm0417.png) |
As with the CONTRAST transformation, if you want to omit a level other than the last, you can specify it in parentheses after the keyword MEAN in the REPEATED statement.
PROFILE Transformation
When a repeated measure represents a series of factors administered over time, but a polynomial response is unreasonable, a profile transformation might prove useful. As an example, consider a training program in which four different methods are employed to teach students at several different schools. The repeated measure is the score on tests administered after each of the methods is completed. The statements
proc glm; class school; model t1-t4=school / nouni; repeated method 4 profile / summary nom printm; run;
produce the following ![]() matrix:
matrix:
![\[ \mb {M} = \left[ \begin{array}{rrrr} 1 & -1 & 0 & 0 \\ 0 & 1 & -1 & 0 \\ 0 & 0 & 1 & -1 \\ \end{array} \right] \]](images/statug_glm0418.png) |
To determine the point at which an improvement in test scores takes place, you can examine the analyses of variance for the transformed variables representing the differences between adjacent tests. These analyses are requested by the SUMMARY option in the REPEATED statement, and the variables are labeled METHOD.1, METHOD.2, and METHOD.3.