The CANDISC Procedure
Example 29.1 Analysis of Iris Data With PROC CANDISC
The iris data published by Fisher (1936) have been widely used for examples in discriminant analysis and cluster analysis. The sepal length, sepal width, petal length,
and petal width are measured in millimeters on 50 iris specimens from each of three species: Iris setosa, I. versicolor, and I. virginica. The iris data set is available from the Sashelp library.
This example is a canonical discriminant analysis that creates an output data set containing scores on the canonical variables and plots the canonical variables.
The following statements produce Output 29.1.1 through Output 29.1.6:
title 'Fisher (1936) Iris Data'; proc candisc data=sashelp.iris out=outcan distance anova; class Species; var SepalLength SepalWidth PetalLength PetalWidth; run;
PROC CANDISC first displays information about the observations and the classes in the data set in Output 29.1.1.
Output 29.1.1: Iris Data: Summary Information
| Fisher (1936) Iris Data |
| Total Sample Size | 150 | DF Total | 149 |
|---|---|---|---|
| Variables | 4 | DF Within Classes | 147 |
| Classes | 3 | DF Between Classes | 2 |
| Number of Observations Read | 150 |
|---|---|
| Number of Observations Used | 150 |
| Class Level Information | ||||
|---|---|---|---|---|
| Species | Variable Name |
Frequency | Weight | Proportion |
| Setosa | Setosa | 50 | 50.0000 | 0.333333 |
| Versicolor | Versicolor | 50 | 50.0000 | 0.333333 |
| Virginica | Virginica | 50 | 50.0000 | 0.333333 |
The DISTANCE option in the PROC CANDISC statement displays squared Mahalanobis distances between class means. Results from the DISTANCE option are shown in Output 29.1.2.
Output 29.1.2: Iris Data: Squared Mahalanobis Distances and Distance Statistics
| Fisher (1936) Iris Data |
| Squared Distance to Species | |||
|---|---|---|---|
| From Species | Setosa | Versicolor | Virginica |
| Setosa | 0 | 89.86419 | 179.38471 |
| Versicolor | 89.86419 | 0 | 17.20107 |
| Virginica | 179.38471 | 17.20107 | 0 |
| F Statistics, NDF=4, DDF=144 for Squared Distance to Species |
|||
|---|---|---|---|
| From Species | Setosa | Versicolor | Virginica |
| Setosa | 0 | 550.18889 | 1098 |
| Versicolor | 550.18889 | 0 | 105.31265 |
| Virginica | 1098 | 105.31265 | 0 |
| Prob > Mahalanobis Distance for Squared Distance to Species |
|||
|---|---|---|---|
| From Species | Setosa | Versicolor | Virginica |
| Setosa | 1.0000 | <.0001 | <.0001 |
| Versicolor | <.0001 | 1.0000 | <.0001 |
| Virginica | <.0001 | <.0001 | 1.0000 |
The ANOVA option uses univariate statistics to test the hypothesis that the class means are equal. The resulting R-square
values (see Output 29.1.3) range from 0.4008 for SepalWidth to 0.9414 for PetalLength, and each variable is significant at the 0.0001 level. The multivariate test for differences between the classes (which is
displayed by default) is also significant at the 0.0001 level; you would expect this from the highly significant univariate
test results.
Output 29.1.3: Iris Data: Univariate and Multivariate Statistics
| Fisher (1936) Iris Data |
| Univariate Test Statistics | ||||||||
|---|---|---|---|---|---|---|---|---|
| F Statistics, Num DF=2, Den DF=147 | ||||||||
| Variable | Label | Total Standard Deviation |
Pooled Standard Deviation |
Between Standard Deviation |
R-Square | R-Square / (1-RSq) |
F Value | Pr > F |
| SepalLength | Sepal Length (mm) | 8.2807 | 5.1479 | 7.9506 | 0.6187 | 1.6226 | 119.26 | <.0001 |
| SepalWidth | Sepal Width (mm) | 4.3587 | 3.3969 | 3.3682 | 0.4008 | 0.6688 | 49.16 | <.0001 |
| PetalLength | Petal Length (mm) | 17.6530 | 4.3033 | 20.9070 | 0.9414 | 16.0566 | 1180.16 | <.0001 |
| PetalWidth | Petal Width (mm) | 7.6224 | 2.0465 | 8.9673 | 0.9289 | 13.0613 | 960.01 | <.0001 |
| Average R-Square | |
|---|---|
| Unweighted | 0.7224358 |
| Weighted by Variance | 0.8689444 |
| Multivariate Statistics and F Approximations | |||||
|---|---|---|---|---|---|
| S=2 M=0.5 N=71 | |||||
| Statistic | Value | F Value | Num DF | Den DF | Pr > F |
| Wilks' Lambda | 0.02343863 | 199.15 | 8 | 288 | <.0001 |
| Pillai's Trace | 1.19189883 | 53.47 | 8 | 290 | <.0001 |
| Hotelling-Lawley Trace | 32.47732024 | 582.20 | 8 | 203.4 | <.0001 |
| Roy's Greatest Root | 32.19192920 | 1166.96 | 4 | 145 | <.0001 |
| NOTE: F Statistic for Roy's Greatest Root is an upper bound. | |||||
| NOTE: F Statistic for Wilks' Lambda is exact. | |||||
The R square between Can1 and the class variable, 0.969872, is much larger than the corresponding R square for Can2, 0.222027. This is displayed in Output 29.1.4.
Output 29.1.4: Iris Data: Canonical Correlations and Eigenvalues
| Fisher (1936) Iris Data |
| Canonical Correlation |
Adjusted Canonical Correlation |
Approximate Standard Error |
Squared Canonical Correlation |
Eigenvalues of Inv(E)*H = CanRsq/(1-CanRsq) |
Test of H0: The canonical correlations in the current row and all that follow are zero | ||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Eigenvalue | Difference | Proportion | Cumulative | Likelihood Ratio |
Approximate F Value |
Num DF | Den DF | Pr > F | |||||
| 1 | 0.984821 | 0.984508 | 0.002468 | 0.969872 | 32.1919 | 31.9065 | 0.9912 | 0.9912 | 0.02343863 | 199.15 | 8 | 288 | <.0001 |
| 2 | 0.471197 | 0.461445 | 0.063734 | 0.222027 | 0.2854 | 0.0088 | 1.0000 | 0.77797337 | 13.79 | 3 | 145 | <.0001 | |
Output 29.1.5: Iris Data: Correlations between Canonical and Original Variables
| Fisher (1936) Iris Data |
| Total Canonical Structure | |||
|---|---|---|---|
| Variable | Label | Can1 | Can2 |
| SepalLength | Sepal Length (mm) | 0.791888 | 0.217593 |
| SepalWidth | Sepal Width (mm) | -0.530759 | 0.757989 |
| PetalLength | Petal Length (mm) | 0.984951 | 0.046037 |
| PetalWidth | Petal Width (mm) | 0.972812 | 0.222902 |
| Between Canonical Structure | |||
|---|---|---|---|
| Variable | Label | Can1 | Can2 |
| SepalLength | Sepal Length (mm) | 0.991468 | 0.130348 |
| SepalWidth | Sepal Width (mm) | -0.825658 | 0.564171 |
| PetalLength | Petal Length (mm) | 0.999750 | 0.022358 |
| PetalWidth | Petal Width (mm) | 0.994044 | 0.108977 |
| Pooled Within Canonical Structure | |||
|---|---|---|---|
| Variable | Label | Can1 | Can2 |
| SepalLength | Sepal Length (mm) | 0.222596 | 0.310812 |
| SepalWidth | Sepal Width (mm) | -0.119012 | 0.863681 |
| PetalLength | Petal Length (mm) | 0.706065 | 0.167701 |
| PetalWidth | Petal Width (mm) | 0.633178 | 0.737242 |
The raw canonical coefficients (shown in Output 29.1.6) for the first canonical variable, Can1, show that the classes differ most widely on the linear combination of the centered variables: ![]() .
.
Output 29.1.6: Iris Data: Canonical Coefficients
| Fisher (1936) Iris Data |
| Total-Sample Standardized Canonical Coefficients | |||
|---|---|---|---|
| Variable | Label | Can1 | Can2 |
| SepalLength | Sepal Length (mm) | -0.686779533 | 0.019958173 |
| SepalWidth | Sepal Width (mm) | -0.668825075 | 0.943441829 |
| PetalLength | Petal Length (mm) | 3.885795047 | -1.645118866 |
| PetalWidth | Petal Width (mm) | 2.142238715 | 2.164135931 |
| Pooled Within-Class Standardized Canonical Coefficients | |||
|---|---|---|---|
| Variable | Label | Can1 | Can2 |
| SepalLength | Sepal Length (mm) | -.4269548486 | 0.0124075316 |
| SepalWidth | Sepal Width (mm) | -.5212416758 | 0.7352613085 |
| PetalLength | Petal Length (mm) | 0.9472572487 | -.4010378190 |
| PetalWidth | Petal Width (mm) | 0.5751607719 | 0.5810398645 |
| Raw Canonical Coefficients | |||
|---|---|---|---|
| Variable | Label | Can1 | Can2 |
| SepalLength | Sepal Length (mm) | -.0829377642 | 0.0024102149 |
| SepalWidth | Sepal Width (mm) | -.1534473068 | 0.2164521235 |
| PetalLength | Petal Length (mm) | 0.2201211656 | -.0931921210 |
| PetalWidth | Petal Width (mm) | 0.2810460309 | 0.2839187853 |
Output 29.1.7: Iris Data: Canonical Means
| Class Means on Canonical Variables | ||
|---|---|---|
| Species | Can1 | Can2 |
| Setosa | -7.607599927 | 0.215133017 |
| Versicolor | 1.825049490 | -0.727899622 |
| Virginica | 5.782550437 | 0.512766605 |
The TEMPLATE and SGRENDER procedures are used to create a plot of the first two canonical variables. The following statements produce Output 29.1.8:
proc template;
define statgraph scatter;
begingraph;
entrytitle 'Fisher (1936) Iris Data';
layout overlayequated / equatetype=fit
xaxisopts=(label='Canonical Variable 1')
yaxisopts=(label='Canonical Variable 2');
scatterplot x=Can1 y=Can2 / group=species name='iris';
layout gridded / autoalign=(topleft);
discretelegend 'iris' / border=false opaque=false;
endlayout;
endlayout;
endgraph;
end;
run;
proc sgrender data=outcan template=scatter;
run;
Output 29.1.8: Iris Data: Plot of First Two Canonical Variables
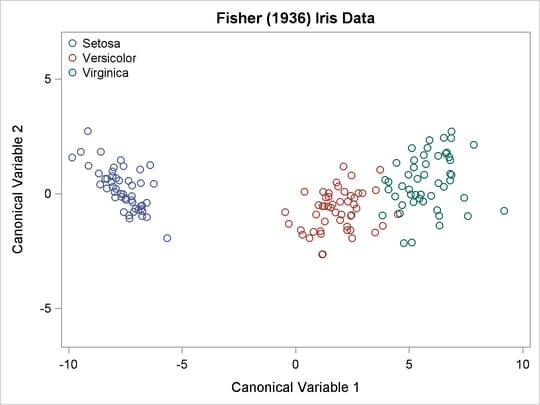
The plot of canonical variables in Output 29.1.8 shows that of the two canonical variables, Can1 has more discriminatory power.
