The STDIZE Procedure
| Computing Quantiles |
PROC STDIZE offers two methods for computing quantiles: the one-pass approach and the order-statistics approach (like that used in the UNIVARIATE procedure).
The one-pass approach used in PROC STDIZE modifies the  algorithm for histograms proposed by Jain and Chlamtac (1985). The primary difference comes from the movement of markers. The one-pass method allows a marker to move to the right (or left) by more than one position (to the largest possible integer) as long as it does not result in two markers being in the same position. The modification is necessary in order to incorporate the FREQ variable.
algorithm for histograms proposed by Jain and Chlamtac (1985). The primary difference comes from the movement of markers. The one-pass method allows a marker to move to the right (or left) by more than one position (to the largest possible integer) as long as it does not result in two markers being in the same position. The modification is necessary in order to incorporate the FREQ variable.
You might obtain inaccurate results if you use the one-pass approach to estimate quantiles beyond the quartiles (that is, when you estimate quantiles < P25 or quantiles > P75). A large sample size (10,000 or more) is often required if the tail quantiles (quantiles 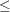 P10 or quantiles
P10 or quantiles  P90) are requested. Note that, for variables with highly skewed or heavy-tailed distributions, tail quantile estimates might be inaccurate.
P90) are requested. Note that, for variables with highly skewed or heavy-tailed distributions, tail quantile estimates might be inaccurate.
The order-statistics approach for estimating quantiles is faster than the one-pass method but requires that the entire data set be stored in memory. The accuracy in estimating the quantiles is comparable for both methods when the requested percentiles are between the lower and upper quartiles. The default is PCTLMTD=ORD_STAT if enough memory is available; otherwise, PCTLMTD=ONEPASS.
Computational Methods for the PCTLDEF= Option
You can specify one of five methods for computing quantile statistics when you use the order-statistics approach (PCTLMTD=ORD_STAT); otherwise, the PCTLDEF=5 method is used when you use the one-pass approach (PCTLMTD=ONEPASS).
Percentile Definitions
Let n be the number of nonmissing values for a variable, and let 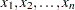 represent the ordered values of the variable. For the tth percentile, let
represent the ordered values of the variable. For the tth percentile, let 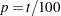 . In the following definitions numbered 1, 2, 3, and 5, let
. In the following definitions numbered 1, 2, 3, and 5, let
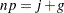 |
where j is the integer part and g is the fractional part of 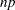 . For definition 4, let
. For definition 4, let
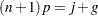 |
Given the preceding definitions, the tth percentile, y, is defined as follows:
- PCTLDEF=1
-
weighted average at
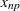

where
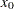 is taken to be
is taken to be 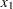
- PCTLDEF=2
-
observation numbered closest to
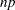

where i is the integer part of
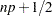 if
if 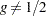 . If
. If  , then
, then 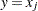 if j is even, or
if j is even, or 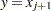 if j is odd
if j is odd - PCTLDEF=3
-
empirical distribution function
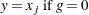
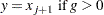
- PCTLDEF=4
-
weighted average aimed at
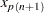
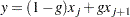
where
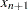 is taken to be
is taken to be 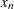
- PCTLDEF=5
-
empirical distribution function with averaging
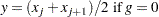
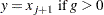
Weighted Percentiles
When you specify a WEIGHT statement, or specify the NOTRUNCATE option in a FREQ statement, the percentiles are computed differently. The 100pth weighted percentile y is computed from the empirical distribution function with averaging
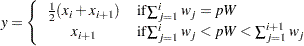 |
where 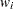 is the weight associated with
is the weight associated with 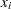 , and where
, and where 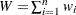 is the sum of the weights.
is the sum of the weights.
For PCTLMTD= ORD_STAT, the PCTLDEF= option is not applicable when a WEIGHT statement is used, or when a NOTRUNCATE option is specified in a FREQ statement. However, in this case, if all the weights are identical, the weighted percentiles are the same as the percentiles that would be computed without a WEIGHT statement and with PCTLDEF=5.
For PCTLMTD= ONEPASS, the quantile computation currently does not use any weights.
