The SIM2D Procedure
Example 82.3 Risk Analysis with Simulation
This example is in the field of environmental risk assessment. A square region of size 500 km  500 km has been sampled for arsenic in drinking water. The logAsData data set consists of 138 simulated arsenic logarithm concentration observations represented by the logAs variable. Section Aspects of Semivariogram Model Fitting in the VARIOGRAM procedure treats these observations as actual data in order to determine the spatial continuity structure for illustration in the examples.
500 km has been sampled for arsenic in drinking water. The logAsData data set consists of 138 simulated arsenic logarithm concentration observations represented by the logAs variable. Section Aspects of Semivariogram Model Fitting in the VARIOGRAM procedure treats these observations as actual data in order to determine the spatial continuity structure for illustration in the examples.
A preliminary analysis indicates that the population exposure to the pollutant is currently at a relatively low level, as shown in the section Spatial Prediction of Pollutant Concentration in the KRIGE2D procedure. In particular, spatial prediction with kriging suggests that less than 1% of the region is affected by arsenic concentration in water that exceeds the World Health Organization (WHO) standard of 10  g/lt.
g/lt.
You want to simulate the random field of the arsenic logarithm concentration so that you can gain insight into the characteristics of this field. Your objective is to assess whether the occurrence of above-threshold arsenic concentrations is a localized phenomenon, and whether you might expect more such occurrences across the region. For the simulation you need the outcome of the spatial continuity analysis in section Aspects of Semivariogram Model Fitting in the VARIOGRAM procedure. These results are the fitted semivariance models that are stored in the SemivAsStore item store by PROC VARIOGRAM.
Based on the discussion in the section Simulation and Economic Feasibility, you simulate the arsenic logarithm concentration on the premise of the ergodicity assumption. In brief, this assumption relates the mean and covariances of each individual realization to the corresponding values of the random field; see also the section Ergodicity in the VARIOGRAM procedure. In the present case you are interested in the average of a large size of realizations, rather than individual ones. A single realization could suggest possible locations where the WHO regulatory standard might be violated. The average of multiple realizations has a smoothing effect on individual excessive-concentration episodes in single realizations. The smoothing enables you to see general characteristics of the arsenic concentration field behavior on the basis of its spatial correlation description.
For illustration, assume a rectangular grid of nodes with an equal spacing of 10 km between neighboring nodes in the north and east directions. Then, simulated values are produced at a total of  locations.
locations.
You begin by reading the logAsData data set with the following DATA step:
title 'Risk Assessment with Simulation';
data logAsData;
input East North logAs @@;
label logAs='log(As) Concentration';
datalines;
193.0 296.6 -0.68153 232.6 479.1 0.96279 268.7 312.5 -1.02908
43.6 4.9 0.65010 152.6 54.9 1.87076 449.1 395.8 0.95932
310.9 493.6 -1.66208 287.8 164.9 -0.01779 330.0 8.0 2.06837
225.7 241.7 0.15899 452.3 83.4 -1.21217 156.5 462.5 -0.89031
11.5 84.4 -0.24496 144.4 335.7 0.11950 149.0 431.8 -0.57251
234.3 123.2 -1.33642 37.8 197.8 -0.27624 183.1 173.9 -2.14558
149.3 426.7 -1.06506 434.4 67.5 -1.04657 439.6 237.0 -0.09074
36.4 175.2 -1.21211 370.6 244.0 3.28091 452.0 96.5 -0.77081
247.0 86.8 0.04720 413.6 373.2 1.78235 253.5 291.7 0.56132
129.7 111.9 1.34000 352.7 42.1 0.23621 279.3 82.7 2.12350
382.6 290.7 0.86756 188.2 222.8 -1.23308 382.8 154.5 -0.94094
304.4 309.2 -1.95158 337.5 387.2 -1.31294 490.7 189.8 0.40206
159.0 100.1 -0.22272 245.5 329.2 -0.26082 372.1 379.5 -1.89078
417.8 84.1 -1.25176 173.9 407.6 -0.24240 121.5 107.7 1.54509
453.5 313.6 0.65895 143.5 346.7 -0.87196 157.4 125.5 -1.96165
371.8 353.2 -0.59464 358.9 338.2 -1.07133 8.6 437.8 1.44203
395.9 394.2 -0.24144 149.5 58.9 1.17459 453.5 420.6 -0.63951
182.3 85.0 1.00005 21.0 290.1 0.31016 11.1 352.2 -0.88418
131.2 238.4 -0.57184 104.9 6.3 1.12054 247.3 256.0 0.14019
428.4 383.7 0.92448 327.8 481.1 -2.72543 199.2 92.8 -0.05717
453.9 230.1 0.16571 205.0 250.6 0.07581 459.5 271.6 0.93700
229.5 262.8 1.83590 370.4 228.6 2.96611 330.2 281.9 1.79723
354.8 388.3 -3.18262 406.2 222.7 2.41594 254.4 393.1 2.03221
96.7 85.2 -0.47156 407.2 256.8 0.66747 498.5 273.8 1.03041
417.2 471.4 -1.42766 368.8 424.3 -0.70506 303.0 59.1 1.43070
403.1 264.1 1.64554 21.2 360.8 0.67094 148.2 78.1 2.15323
305.5 310.7 -1.47985 228.5 180.3 -0.68386 161.1 143.3 1.07901
70.5 155.1 0.54652 363.1 282.6 -0.43051 86.0 472.5 -1.18855
175.9 105.3 -2.08112 96.8 426.3 1.56592 475.1 453.1 -1.53776
125.7 485.4 1.40054 277.9 201.6 -0.54565 406.2 125.0 -1.38657
60.0 275.5 -0.59966 431.3 494.6 -0.36860 399.9 399.0 -0.77265
28.8 311.1 0.91693 166.1 348.2 -0.49056 266.6 83.5 0.67277
54.7 356.3 0.49596 433.5 460.3 -1.61309 201.7 167.6 -1.40678
158.1 203.6 -1.32499 67.6 230.4 1.14672 81.9 250.0 0.63378
372.0 50.7 0.72445 26.4 264.6 1.00862 300.1 91.7 -0.74089
303.0 447.4 1.74589 108.4 386.2 1.12847 55.6 191.7 0.95175
36.3 273.2 1.78880 94.5 298.3 -2.43320 366.1 187.3 -0.80526
130.7 389.2 -0.31513 37.2 324.2 0.24489 295.5 211.8 0.41899
58.6 206.2 0.18495 346.3 142.8 -0.92038 484.2 215.9 0.08012
451.4 415.7 0.02773 58.9 86.5 0.17652 212.6 363.9 0.17215
378.7 407.6 0.51516 265.9 305.0 -0.30718 123.2 314.8 -0.90591
26.9 471.7 1.70285 16.5 7.1 0.51736 255.1 472.6 2.02381
111.5 148.4 -0.09658 440.4 375.0 1.23285 406.4 19.5 1.01181
321.2 65.8 -0.02095 466.4 357.1 -0.49272 2.0 484.6 0.50994
200.9 205.1 0.43543 30.3 337.0 1.60882 297.0 12.7 1.79824
158.2 450.7 0.05295 122.8 105.3 1.53936 417.8 329.7 -2.08124
;
For this simulation you use the spatial correlation information that is saved in the SemivAsStore item store in the section Aspects of Semivariogram Model Fitting in the VARIOGRAM procedure with the following statements:
ods graphics on;
proc variogram data=logAsData plots=none; store out=SemivAsStore / label='LogAs Concentration Models'; compute lagd=5 maxlag=40; coord xc=East yc=North; model form=auto(mlist=(exp,gau,mat) nest=1 to 2); var logAs; run;
In PROC SIM2D you specify the container item store with the IN= option of the RESTORE statement. You request correlation input from an item store by specifying the STORESELECT option in the SIMULATE statement. You request 5,000 realizations for this simulation by specifying the number in the NUMREAL= option of the SIMULATE statement.
Assume that you first want to review the saved models in the item store. Use the INFO option of the RESTORE statement to produce a table with information about the top-ranking fitted model in the item store. Use the DET and ONLY suboptions of the INFO option to request details about all fitted models included in the item store. The ONLY suboption suppresses the simulation tasks and produces only the tables about the item store. You specify the following statements:
proc sim2d data=logAsData outsim=Outsim plots=none; restore in=SemivAsStore / info(det only); coordinates xc=East yc=North; simulate var=logAs numreal=5000 storeselect seed=39841; grid x=0 to 500 by 10 y=0 to 500 by 10; run;
PROC SIM2D produces a table with general information about the input item store identity, as shown in Output 82.3.1.
| Risk Assessment with Simulation |
| Correlation Model Item Store Information | |
|---|---|
| Input Item Store | WORK.SEMIVASSTORE |
| Item Store Label | LogAs Concentration Models |
| Data Set Created From | WORK.LOGASDATA |
| By-group Information | No By-groups Present |
| Created By | PROC VARIOGRAM |
| Date Created | 12JAN11:12:16:01 |
Output 82.3.2 displays the item store variables, in addition to the mean and standard deviation of their data set of origin. In this case, the logAs values come from the logAsData data set. By default, the SIM2D procedure uses the variable mean in the item store for the simulation, unless you explicitly specify the MEAN statement.
| Item Store Variables | ||
|---|---|---|
| Variable | Mean | Std Deviation |
| logAs | 0.084309 | 1.527707 |
The models in the SemivAsStore item store that have been fitted to the arsenic logarithm logAs empirical semivariance are shown in Output 82.3.3. The default item store model selection is the model on top of the list in Output 82.3.3.
| Item Store Models For logAs |
|
|---|---|
| Class | Model |
| 1 | Gau-Gau |
| Gau-Mat | |
| 2 | Exp-Gau |
| 3 | Exp-Mat |
| 4 | Mat |
| 5 | Gau |
| 6 | Exp |
| Exp-Exp | |
| Mat-Exp | |
| Gau-Exp | |
You run again the SIM2D procedure without the INFO option in the RESTORE statement. This action prompts PROC SIM2D to run the simulation tasks that you specify with the SIMULATE statement. You specify the STORESELECT option in the SIMULATE statement without any suboptions, so that the simulation uses the default model selection in the SemivAsStore item store. You save the simulation output in the Outsim output data set. You also specify the SIM and the SEMIVAR suboptions in the PLOTS option of the PROC SIM2D statement to obtain output plots. You use the following statements:
proc sim2d data=logAsData outsim=Outsim plots=(sim semivar); restore in=SemivAsStore; coordinates xc=East yc=North; simulate var=logAs numreal=5000 storeselect seed=89702; grid x=0 to 500 by 10 y=0 to 500 by 10; run;
Note: This step can take several minutes to run, and it produces a data set with over 10 million observations. When you run these statements, PROC SIM2D again produces a table about the input item store identity. This output is followed by a number of observations table and information about the simulation task, as shown in Output 82.3.4.
| Risk Assessment with Simulation |
| Number of Observations Read | 138 |
|---|---|
| Number of Observations Used | 138 |
| Simulation Information | |
|---|---|
| Simulation Grid Points | 2601 |
| Type | Conditional |
| Number of Realizations | 5000 |
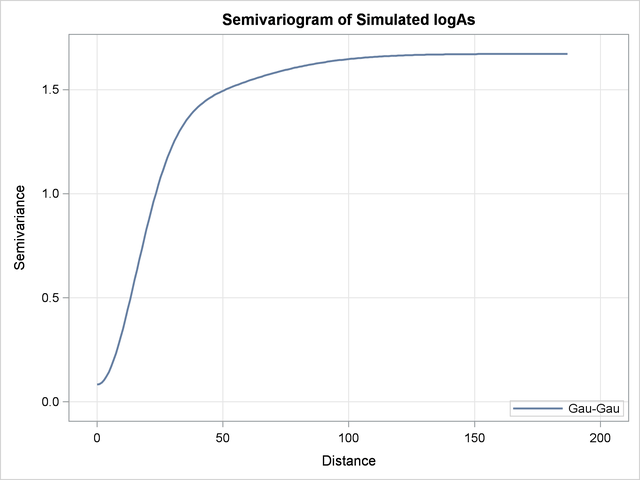
The SIM2D procedure uses the selected fitted Gaussian-Gaussian model in the SemivAsStore item store. Output 82.3.5 shows the saved parameter values of the model that are used in the simulation.
| Covariance Model Information | |
|---|---|
| Nested Structure 1 Type | Gaussian |
| Nested Structure 1 Sill | 0.3276646 |
| Nested Structure 1 Range | 62.312728 |
| Nested Structure 1 Effective Range | 107.92881 |
| Nested Structure 2 Type | Gaussian |
| Nested Structure 2 Sill | 1.261545 |
| Nested Structure 2 Range | 21.459563 |
| Nested Structure 2 Effective Range | 37.169053 |
| Nugget Effect | 0.0830758 |
Output 82.3.6 shows a plot of the correlation model used in the simulation. Its parameters come from the stored information in the SemivAsStore item store.
The PLOTS=SIM option produces contours of the mean value of the 5,000 realizations for each one of the output grid locations, and a surface of the associated standard deviation. The resulting plot is shown in Output 82.3.7. The mean value contours exhibit reduced variation compared to a SIM plot of one single realization. In fact, Output 82.3.7 is very similar to the prediction plot of the same Gaussian model in the section Spatial Prediction of Pollutant Concentration in the KRIGE2D procedure.
Clearly, there appears to be a small area of increased arsenic concentration values, which is located in the central-eastern part of the domain. The WHO threshold of 10  g/lt for the maximum allowed arsenic concentration in water translates into about 2.3 in the log scale. The indicated area is the only one within the region where the simulated means exceed the value 3. In addition, there appear to be two smaller areas of simulated means values at or above 2 in the southern part of the region.
g/lt for the maximum allowed arsenic concentration in water translates into about 2.3 in the log scale. The indicated area is the only one within the region where the simulated means exceed the value 3. In addition, there appear to be two smaller areas of simulated means values at or above 2 in the southern part of the region.
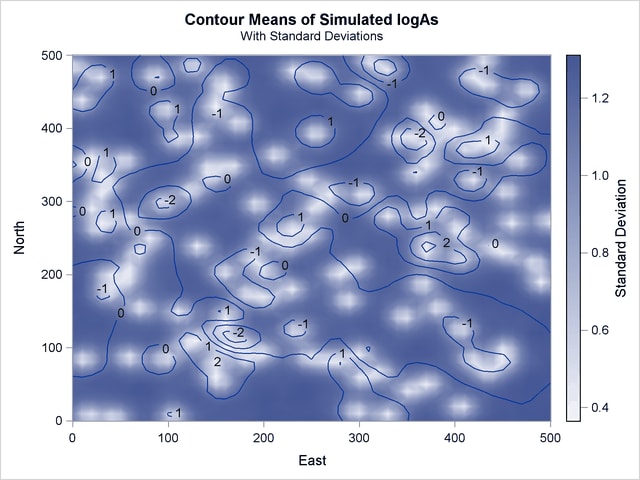
The simulation plot indicates that arsenic concentration values in excess of the WHO health standard is a rather localized phenomenon. If it were not so, then the plot would suggest that increased arsenic concentrations extend across larger areas. In turn, this means that individual realizations would tend to produce systematically higher arsenic concentrations at different neighboring locations, and their average would appear as higher logAs values in the SIM plot. Instead, you conclude that the Gaussian-Gaussian correlation that describes the spatial continuity for the arsenic logarithm observations leads to only localized occurrence of the WHO standard violation.
Now you want to find out whether additional localized occurrences might take place on the basis of the Gaussian-Gaussian spatial continuity behavior. The distribution of the simulation standard deviation values in Output 82.3.7 offers important feedback about this issue. Observe the areas in the plot where the means gradient indicates increasing values. The means contours create several pools where the values increase to simulated means higher than 1.
With the clear exceptions of the isolated area in the central-eastern part of the domain and the pool in the south-west that exhibit logAs values above 2, the simulation standard deviation seems to be around 1 or less in almost all other pools with logAs values above 1. Due to those relatively low standard deviations, this visual inspection suggests that even in individual realizations you might rarely expect the arsenic logarithm to exceed the threshold value of around 2.3.
However, in the few pools of logAs values above 1, there can be patches of increased standard deviation. In these cases, you suspect that arsenic concentration could exceed occasionally the WHO regulatory standard, even if the plot of the simulated means does not explicitly portray so.
Based on these remarks, you want to quantify the percentage of the region that could be affected by excessive arsenic concentration. You begin with a DATA step that takes as input the simulation Outsim output data set. The DATA step marks the simulated arsenic logarithm means values that are in excess of the WHO concentration threshold of 10  g/lt, and saves the outcome into an indicator variable OverLimit. At the same time, the arsenic logarithm values are transformed back into arsenic concentration values so that they can be compared to the threshold value. The simulated means in the Outsim data set are stored in the svalue variable. You use the following statements:
g/lt, and saves the outcome into an indicator variable OverLimit. At the same time, the arsenic logarithm values are transformed back into arsenic concentration values so that they can be compared to the threshold value. The simulated means in the Outsim data set are stored in the svalue variable. You use the following statements:
data AsOverLimit; set Outsim; OverLimit = (exp(svalue) > 10) * 100; run;
Then, you use the MEANS procedure to express the selected nodes population (where the WHO standard violation occurs) as a percentage of the entire domain area. You invoke PROC MEANS twice. The first time, you average over each realization in the PROC SIM2D output. For that purpose, you use the variable _ITER_ in the simulation sim1 output data set as a BY variable in PROC MEANS. You save the iteration-averaged indicator values in the PctOverLimit variable. The second time, PROC MEANS averages the PctOverLimit variable to obtain the percentage you want. You also specify the P5 and P95 options in the PROC MEANS statement to request the lower and upper confidence limits, respectively, in this computation. The interval between those limits expresses the 90% interval for the true area percentage based on the stochastic simulation. You use the following statements:
proc means data=AsOverLimit noprint; by _ITER_; var OverLimit; output out=OverLimitData mean=PctOverLimit; proc means data=OverLimitData mean p5 p95; var PctOverLimit; label PctOverLimit="Percent above threshold"; run;
The result is shown in Output 82.3.8. PROC MEANS accounts for all individual occurrences throughout the simulation where the WHO arsenic concentration threshold is exceeded. This happens at about 3.9% of the total area in 5,000 realizations. Compare this value to the less than 1% percentage in the PROC KRIGE2D prediction, as reported in the beginning of this section. On one hand, the prediction outcome tells you what goes on currently across the region within a degree of certainty given by the prediction error. On the other hand, the simulation provides you with an indicator that under the given spatial continuity estimate a relatively larger area is in potential danger of being affected by above-threshold arsenic concentration.
In fact, the 5% and 95% confidence limits in Output 82.3.8 show the area percentage limits within which you can expect excessive arsenic concentration. Based on the stochastic simulation, at the 90% confidence level the arsenic concentration in drinking water is expected to violate the WHO regulatory standard in anywhere from about 2.6% to 5.4% of the study region.
| Risk Assessment with Simulation |
| Analysis Variable : PctOverLimit Percent above threshold |
||
|---|---|---|
| Mean | 5th Pctl | 95th Pctl |
| 3.9308727 | 2.6143791 | 5.4209919 |
You also want to compute the probability that individual areas in the region are expected to violate the WHO arsenic concentration standard. Start by identifying again the simulated arsenic logarithm means values in excess of the WHO concentration threshold of 10  g/lt. The following DATA step saves the outcome into the variable LocalOverLimit:
g/lt. The following DATA step saves the outcome into the variable LocalOverLimit:
data LocalAsOverLimit; set Outsim; LocalOverLimit = (exp(svalue) > 10); run;
Then you use the SORT procedure to sort the information based on location coordinates. This intermediate step is necessary so that you can use the MEANS procedure with the LocalAsOverLimit data set. In the following statements, PROC MEANS computes the expected violations of the WHO standard for each location in the region across all realizations of the simulation:
proc sort data=LocalAsOverLimit; by gxc gyc; proc means data=LocalAsOverLimit noprint; by gxc gyc; var LocalOverLimit; output out=OverLimLoci mean=ProbOverLimit; run;
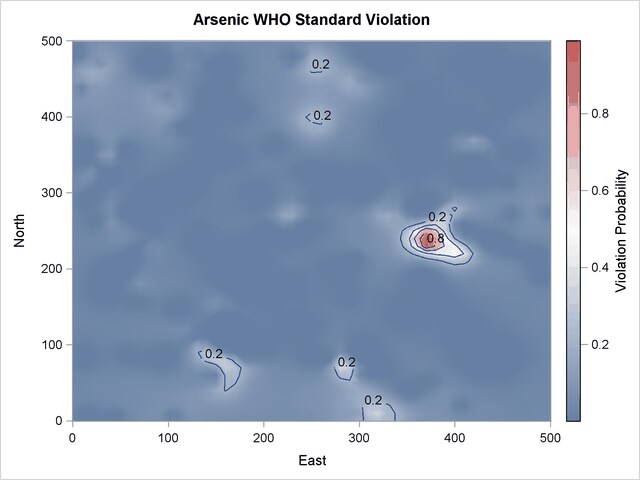
The output is the probability that the WHO standard is violated at each one of the simulation locations across the region. You create a plot of this probability with the help of the TEMPLATE and the SGRENDER procedures. You use the following statements:
proc template;
define statgraph surfacePlot;
dynamic _VARX _VARY _VAR _TITLE _LEGENDLABEL;
BeginGraph;
entrytitle _TITLE;
layout overlay /
xaxisopts = (offsetmax=0)
yaxisopts = (offsetmax=0);
contourplotparm x=_VARX y=_VARY z=_VAR /
nhint=10 name='probplot';
continuouslegend 'probplot' / title=_LEGENDLABEL;
endlayout;
EndGraph;
end;
run;
proc sgrender data=OverLimLoci template=surfacePlot;
dynamic _VARX ='gxc'
_VARY ='gyc'
_VAR ='ProbOverLimit'
_TITLE='Arsenic WHO Standard Violation'
_LEGENDLABEL='Violation Probability';
label gyc='North' gxc='East';
run;
ods graphics off;
Output 82.3.9 shows the map of probability that the arsenic concentration WHO standard is violated in the region for the selected spatial correlation model of the pollutant. Based on the preceding analysis, the probability is very close to 1 in the area where the simulation mean values are above the standard limit. A few more areas that were indicated earlier in the analysis suggest a violation probability between 20% and 40%. The remaining areas in the region exhibit very low probability, which is notably nonzero at a few scattered locations. These findings suggest that throughout the simulation there have been realizations where the arsenic WHO standard was exceeded at locations whose simulated mean is well below that standard.
From the environmental risk assessment perspective, the preceding analysis can trigger a more detailed investigation into areas in the region where the health standard might be violated. Although the original observations in the logAsData data set indicate no existing problem in some of these areas, the present example illustrates that spatial analysis and simulation can raise flags of caution. This type of analysis can help to focus scientific, management, and policy efforts on these particular areas of the region and to monitor closely the pollutant concentration for potential health risks.