The ROBUSTREG Procedure
Example 77.2 Robust ANOVA
The classical analysis of variance (ANOVA) technique based on least squares assumes that the underlying experimental errors are normally distributed. However, data often contain outliers due to recording or other errors. In other cases, extreme responses occur when control variables in the experiments are set to extremes. It is important to distinguish these extreme points and determine whether they are outliers or important extreme cases. You can use the ROBUSTREG procedure for robust analysis of variance based on M estimation. Typically, there are no high leverage points in a well-designed experiment, so M estimation is appropriate.
The following example shows how to use the ROBUSTREG procedure for robust ANOVA.
An experiment was carried out to study the effects of two successive treatments (T1, T2) on the recovery time of mice with certain diseases. Sixteen mice were randomly assigned into four groups for the four different combinations of the treatments. The recovery times (time) were recorded (in hours) as shown in the following data set recover.
data recover; input T1 $ T2 $ time @@; datalines; 0 0 20.2 0 0 23.9 0 0 21.9 0 0 42.4 1 0 27.2 1 0 34.0 1 0 27.4 1 0 28.5 0 1 25.9 0 1 34.5 0 1 25.1 0 1 34.2 1 1 35.0 1 1 33.9 1 1 38.3 1 1 39.9 ;
The following statements invoke the GLM procedure ( Chapter 41, The GLM Procedure ) for a standard ANOVA:
proc glm data=recover;
class T1 T2;
model time = T1 T2 T1*T2;
run;
| Source | DF | Sum of Squares | Mean Square | F Value | Pr > F |
|---|---|---|---|---|---|
| Model | 3 | 209.9118750 | 69.9706250 | 1.86 | 0.1905 |
| Error | 12 | 451.9225000 | 37.6602083 | ||
| Corrected Total | 15 | 661.8343750 |
| R-Square | Coeff Var | Root MSE | time Mean |
|---|---|---|---|
| 0.317167 | 19.94488 | 6.136791 | 30.76875 |
| Source | DF | Type I SS | Mean Square | F Value | Pr > F |
|---|---|---|---|---|---|
| T1 | 1 | 81.4506250 | 81.4506250 | 2.16 | 0.1671 |
| T2 | 1 | 106.6056250 | 106.6056250 | 2.83 | 0.1183 |
| T1*T2 | 1 | 21.8556250 | 21.8556250 | 0.58 | 0.4609 |
Output 77.2.1 indicates that the overall model effect is not significant at the  level, and Output 77.2.2 indicates that neither treatment is significant at the
level, and Output 77.2.2 indicates that neither treatment is significant at the  level.
level.
The following statements invoke the ROBUSTREG procedure with the same model:
proc robustreg data=recover; class T1 T2; model time = T1 T2 T1*T2 / diagnostics; T1_T2: test T1*T2; output out=robout r=resid sr=stdres; run;
Output 77.2.3 shows some basic information about the model and the response variable time.
| Model Information | |
|---|---|
| Data Set | WORK.RECOVER |
| Dependent Variable | time |
| Number of Independent Variables | 2 |
| Number of Continuous Independent Variables | 0 |
| Number of Class Independent Variables | 2 |
| Number of Observations | 16 |
| Method | M Estimation |
| Summary Statistics | ||||||
|---|---|---|---|---|---|---|
| Variable | Q1 | Median | Q3 | Mean | Standard Deviation |
MAD |
| time | 25.5000 | 31.2000 | 34.7500 | 30.7688 | 6.6425 | 6.8941 |
The "Parameter Estimates" table in Output 77.2.4 indicates that the main effects of both treatments are significant at the 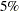 level.
level.
| Parameter Estimates | |||||||||
|---|---|---|---|---|---|---|---|---|---|
| Parameter | DF | Estimate | Standard Error | 95% Confidence Limits | Chi-Square | Pr > ChiSq | |||
| Intercept | 1 | 36.7655 | 2.0489 | 32.7497 | 40.7814 | 321.98 | <.0001 | ||
| T1 | 0 | 1 | -6.8307 | 2.8976 | -12.5100 | -1.1514 | 5.56 | 0.0184 | |
| T1 | 1 | 0 | 0.0000 | . | . | . | . | . | |
| T2 | 0 | 1 | -7.6755 | 2.8976 | -13.3548 | -1.9962 | 7.02 | 0.0081 | |
| T2 | 1 | 0 | 0.0000 | . | . | . | . | . | |
| T1*T2 | 0 | 0 | 1 | -0.2619 | 4.0979 | -8.2936 | 7.7698 | 0.00 | 0.9490 |
| T1*T2 | 0 | 1 | 0 | 0.0000 | . | . | . | . | . |
| T1*T2 | 1 | 0 | 0 | 0.0000 | . | . | . | . | . |
| T1*T2 | 1 | 1 | 0 | 0.0000 | . | . | . | . | . |
| Scale | 1 | 3.5346 | |||||||
The reason for the difference between the traditional ANOVA and the robust ANOVA is explained by Output 77.2.5, which shows that the fourth observation is an outlier. Further investigation shows that the original value of 24.4 for the fourth observation was recorded incorrectly.
Output 77.2.6 displays the robust test results. The interaction between the two treatments is not significant. Output 77.2.7 displays the robust residuals and standardized robust residuals.
| Diagnostics | ||
|---|---|---|
| Obs | Standardized Robust Residual |
Outlier |
| 4 | 5.7722 | * |
| Robust Linear Test T1_T2 | |||||
|---|---|---|---|---|---|
| Test | Test Statistic | Lambda | DF | Chi-Square | Pr > ChiSq |
| Rho | 0.0041 | 0.7977 | 1 | 0.01 | 0.9431 |
| Rn2 | 0.0041 | 1 | 0.00 | 0.9490 | |
| Obs | T1 | T2 | time | resid | stdres |
|---|---|---|---|---|---|
| 1 | 0 | 0 | 20.2 | -1.7974 | -0.50851 |
| 2 | 0 | 0 | 23.9 | 1.9026 | 0.53827 |
| 3 | 0 | 0 | 21.9 | -0.0974 | -0.02756 |
| 4 | 0 | 0 | 42.4 | 20.4026 | 5.77222 |
| 5 | 1 | 0 | 27.2 | -1.8900 | -0.53472 |
| 6 | 1 | 0 | 34.0 | 4.9100 | 1.38911 |
| 7 | 1 | 0 | 27.4 | -1.6900 | -0.47813 |
| 8 | 1 | 0 | 28.5 | -0.5900 | -0.16693 |
| 9 | 0 | 1 | 25.9 | -4.0348 | -1.14152 |
| 10 | 0 | 1 | 34.5 | 4.5652 | 1.29156 |
| 11 | 0 | 1 | 25.1 | -4.8348 | -1.36785 |
| 12 | 0 | 1 | 34.2 | 4.2652 | 1.20668 |
| 13 | 1 | 1 | 35.0 | -1.7655 | -0.49950 |
| 14 | 1 | 1 | 33.9 | -2.8655 | -0.81070 |
| 15 | 1 | 1 | 38.3 | 1.5345 | 0.43413 |
| 16 | 1 | 1 | 39.9 | 3.1345 | 0.88679 |
