The PLAN Procedure
Example 67.5 A Generalized Cyclic Incomplete Block Design
The following statements depict how to create an appropriately randomized generalized cyclic incomplete block design for  treatments (given by the value of t) in
treatments (given by the value of t) in 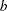 blocks (given by the value of b) of size
blocks (given by the value of b) of size 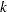 (with values of p indexing the cells within a block) with initial block
(with values of p indexing the cells within a block) with initial block 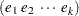 and increment number
and increment number 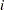 .
.
factors b= |
|
treatments t= |
For example, the specification
proc plan seed=37430; factors b=10 p=4; treatments t=4 of 30 cyclic (1 3 4 26) 2; run;
generates the generalized cyclic incomplete block design given in Example 1 of Jarrett and Hall (1978), which is given by the rows and columns of the plan associated with the treatment factor t in Output 67.5.1.
Output 67.5.1
A Generalized Cyclic Incomplete Block Design
The PLAN Procedure
| Plot Factors | |||
|---|---|---|---|
| Factor | Select | Levels | Order |
| b | 10 | 10 | Random |
| p | 4 | 4 | Random |
| Treatment Factors | ||||
|---|---|---|---|---|
| Factor | Select | Levels | Order | Initial Block / Increment |
| t | 4 | 30 | Cyclic | (1 3 4 26) / 2 |
| b | p | t | ||||||
|---|---|---|---|---|---|---|---|---|
| 2 | 2 | 3 | 1 | 4 | 1 | 3 | 4 | 26 |
| 1 | 3 | 2 | 4 | 1 | 3 | 5 | 6 | 28 |
| 3 | 2 | 3 | 4 | 1 | 5 | 7 | 8 | 30 |
| 10 | 4 | 2 | 3 | 1 | 7 | 9 | 10 | 2 |
| 9 | 4 | 1 | 2 | 3 | 9 | 11 | 12 | 4 |
| 4 | 1 | 3 | 2 | 4 | 11 | 13 | 14 | 6 |
| 5 | 1 | 2 | 4 | 3 | 13 | 15 | 16 | 8 |
| 8 | 3 | 2 | 4 | 1 | 15 | 17 | 18 | 10 |
| 7 | 2 | 4 | 1 | 3 | 17 | 19 | 20 | 12 |
| 6 | 2 | 1 | 4 | 3 | 19 | 21 | 22 | 14 |

 )
)