| Empirical Power Simulation (DATA Step, SAS/STAT Software) |
You can obtain a highly accurate power estimate by simulating the power empirically. You need to use this approach for analyses that are not supported directly in SAS/STAT tools and for which you lack a power formula. But the simulation approach is also a viable alternative to existing power approximations. A high number of simulations will yield a more accurate estimate than a non-exact power approximation.
Although exact power computations for the two-sample t test are supported in several of the SAS/STAT tools, suppose for purposes of illustration that you want to simulate power for the continuing t test example. This section describes how you can use the DATA step and SAS/STAT software to do this.
The simulation involves generating a large number of data sets according to the distributions defined by the power analysis input parameters, computing the relevant 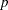 -value for each data set, and then estimating the power as the proportion of times that the
-value for each data set, and then estimating the power as the proportion of times that the 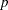 -value is significant.
-value is significant.
The following statements compute a power estimate along with a 95% confidence interval for power for the first scenario in the two-sample t test example, with 10,000 simulations:
%let meandiff = 5;
%let stddev = 12;
%let alpha = 0.05;
%let ntotal = 100;
%let nsim = 10000;
data simdata;
call streaminit(123);
do isim = 1 to ≁
do i = 1 to floor(&ntotal/2);
group = 1;
y = rand('normal', 0 , &stddev);
output;
group = 2;
y = rand('normal', &meandiff, &stddev);
output;
end;
end;
run;
ods listing close;
proc ttest data=simdata;
ods output ttests=tests;
by isim;
class group;
var y;
run;
ods listing;
data tests;
set tests;
where method="Pooled";
issig = probt < α
run;
proc freq data=tests; ods select binomialprop; tables issig / binomial(level='1'); run;
First the DATA step is used to randomly generate nsim=10,000 data sets based on the meandiff, stddev, and ntotal parameters and the normal distribution, consistent with the assumptions underlying the two-sample t test. These data sets are contained in a large SAS data set called simdata indexed by the variable isim.
The CALL STREAMINIT(123) statement initializes the random number generator with a specific sequence and ensures repeatable results for purposes of this example. ( Note: Skip this step when you are performing actual power simulations.)
The TTEST procedure is run using isim as a BY variable, with the ODS LISTING CLOSE statement to suppress output. The ODS OUTPUT statement saves the "TTests" table to a data set called tests. The 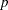 -values are contained in a column called probt.
-values are contained in a column called probt.
The subsequent DATA step defines a variable called issig to flag the significant 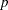 -values.
-values.
Finally, the FREQ procedure computes the empirical power estimate as the estimate of 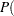 issig
issig 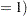 and provides approximate and exact confidence intervals for this estimate.
and provides approximate and exact confidence intervals for this estimate.
Figure 18.7 shows the results. The estimated power is 0.5388 with 95% confidence interval (0.5290, 0.5486). Note that the exact power of 0.541 shown in the first row in Figure 18.1 is contained within this tight confidence interval.
| Binomial Proportion for issig = 1 | |
|---|---|
| Proportion | 0.5388 |
| ASE | 0.0050 |
| 95% Lower Conf Limit | 0.5290 |
| 95% Upper Conf Limit | 0.5486 |
| Exact Conf Limits | |
| 95% Lower Conf Limit | 0.5290 |
| 95% Upper Conf Limit | 0.5486 |