Objective Priors versus Subjective Priors

Bayesian probability measures the degree of belief that you have in a random event. By this definition, probability is highly subjective. It follows that all priors are subjective priors. Not everyone agrees with this notion of subjectivity when it comes to specifying prior distributions. There has long been a desire to obtain results that are objectively valid. Within the Bayesian paradigm, this can be somewhat achieved by using prior distributions that are "objective" (that is, that have a minimal impact on the posterior distribution). Such distributions are called objective or noninformative priors (see the next section). However, while noninformative priors are very popular in some applications, they are not always easy to construct. See DeGroot and Schervish (2002, Section 1.2) and Press (2003, Section 2.2) for more information about interpretations of probability. See Berger (2006) and Goldstein (2006) for discussions about objective Bayesian versus subjective Bayesian analysis.

Noninformative Priors

Roughly speaking, a prior distribution is noninformative if the prior is "flat" relative to the likelihood function. Thus, a prior 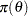is noninformative if it has minimal impact on the posterior distribution of . Other names for the noninformative prior are vague, diffuse, and flat prior. Many statisticians favor noninformative priors because they appear to be more objective. However, it is unrealistic to expect that noninformative priors represent total ignorance about the parameter of interest. In some cases, noninformative priors can lead to improper posteriors (nonintegrable posterior density). You cannot make inferences with improper posterior distributions. In addition, noninformative priors are often not invariant under transformation; that is, a prior might be noninformative in one parameterization but not necessarily noninformative if a transformation is applied.

See Box and Tiao (1973) for a more formal development of noninformative priors. See Kass and Wasserman (1996) for techniques for deriving noninformative priors.

Improper Priors

A prior 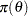is said to be improper if

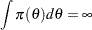For example, a uniform prior distribution on the real line, 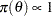, for 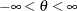, is an improper prior. Improper priors are often used in Bayesian inference since they usually yield noninformative priors and proper posterior distributions. Improper prior distributions can lead to posterior impropriety (improper posterior distribution) . To determine whether a posterior distribution is proper, you need to make sure that the normalizing constant 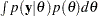is finite for all 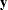. If an improper prior distribution leads to an improper posterior distribution, inference based on the improper posterior distribution is invalid.

The GENMOD, LIFEREG, and PHREG procedures allow the use of improper priors—that is, the flat prior on the real line—for regression coefficients. These improper priors do not lead to any improper posterior distributions in the models that these procedures fit. PROC MCMC allows the use of any prior, as long as the distribution is programmable using DATA step functions. However, the procedure does not verify whether the posterior distribution is integrable. You must ensure this yourself.

Informative Priors

An informative prior is a prior that is not dominated by the likelihood and that has an impact on the posterior distribution. If a prior distribution dominates the likelihood, it is clearly an informative prior. These types of distributions must be specified with care in actual practice. On the other hand, the proper use of prior distributions illustrates the power of the Bayesian method: information gathered from the previous study, past experience, or expert opinion can be combined with current information in a natural way. See the "Examples" sections of the GENMOD and PHREG procedure chapters for instructions about constructing informative prior distributions.

Conjugate Priors

A prior is said to be a conjugate prior for a family of distributions if the prior and posterior distributions are from the same family, which means that the form of the posterior has the same distributional form as the prior distribution. For example, if the likelihood is binomial, 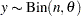, a conjugate prior on is the beta distribution; it follows that the posterior distribution of is also a beta distribution. Other commonly used conjugate prior/likelihood combinations include the normal/normal, gamma/Poisson, gamma/gamma, and gamma/beta cases. The development of conjugate priors was partially driven by a desire for computational convenience—conjugacy provides a practical way to obtain the posterior distributions. The Bayesian procedures do not use conjugacy in posterior sampling.

Jeffreys’ Prior

A very useful prior is Jeffreys’ prior (Jeffreys; 1961). It satisfies the local uniformity property: a prior that does not change much over the region in which the likelihood is significant and does not assume large values outside that range. It is based on the Fisher information matrix. Jeffreys’ prior is defined as

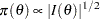where denotes the determinant and 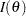is the Fisher information matrix based on the likelihood function :

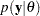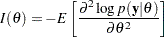Jeffreys’ prior is locally uniform and hence noninformative . It provides an automated scheme for finding a noninformative prior for any parametric model 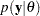. Another appealing property of Jeffreys’ prior is that it is invariant with respect to one-to-one transformations. The invariance property means that if you have a locally uniform prior on and 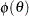is a one-to-one function of , then 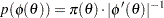is a locally uniform prior for 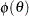. This invariance principle carries through to multidimensional parameters as well. While Jeffreys’ prior provides a general recipe for obtaining noninformative priors, it has some shortcomings: the prior is improper for many models, and it can lead to improper posterior in some cases; and the prior can be cumbersome to use in high dimensions. PROC GENMOD calculates Jeffreys’ prior automatically for any generalized linear model. You can set it as your prior density for the coefficient parameters, and it does not lead to improper posteriors. You can construct Jeffreys’ prior for a variety of statistical models in the MCMC procedure. See the section Logistic Regression Model with Jeffreys’ Prior for an example. PROC MCMC does not guarantee that the corresponding posterior distribution is proper, and you need to exercise extra caution in this case.