The GLMPOWER Procedure
Example 43.2 Two-Way ANOVA with Covariate
Suppose you can enhance the planned study discussed in Example 43.1 in two ways:
incorporate results from races at two different altitudes ("high" and "low")
measure the body mass index of each runner before the race
This is equivalent to adding a second fixed effect and a continuous covariate to your model.
Since lactic acid buildup is more pronounced at higher altitudes, you will include altitude as a factor in the model along with fluid, extending the one-way ANOVA to a two-way ANOVA. In doing so, you expect to lower the residual standard deviation from about 3.75 to 3.5 (in addition to generalizing the study results). You assume there is negligible interaction between fluid and altitude and plan to use a main-effects-only model. You conjecture that the mean lactic acid buildup follows Table 43.10.
Fluid |
|||||
|---|---|---|---|---|---|
Altitude |
Water |
EZD1 |
EZD2 |
LZ1 |
LZ2 |
High |
36.9 |
35.0 |
31.5 |
30 |
27.1 |
Low |
34.3 |
32.4 |
28.9 |
27 |
24.7 |
By including a measurement of body mass index as a covariate in the study, you hope to further reduce the error variability. The extent of this reduction in variability is commonly expressed in two alternative ways: (1) the correlation between the covariates and the response or (2) the proportional reduction in total 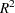 incurred by the covariates. You prefer the former and guess that the correlation between body mass index and lactic acid buildup is between 0.2 and 0.3. You specify these estimates with the NCOVARIATES= and CORRXY= options in the POWER statement. The covariate is not included in the MODEL statement.
incurred by the covariates. You prefer the former and guess that the correlation between body mass index and lactic acid buildup is between 0.2 and 0.3. You specify these estimates with the NCOVARIATES= and CORRXY= options in the POWER statement. The covariate is not included in the MODEL statement.
You are interested in the same four fluid comparisons as in Example 43.1, shown in Table 43.9, except this time you want to marginalize over the effect of altitude.
For each of these contrasts, you want to determine the sample size required to achieve a power of 0.9 to detect an effect with magnitude according to Table 43.10. You are not yet attempting to choose a single sample size for the study, but rather checking the range of sample sizes needed by individual contrasts. You plan to test each contrast at  . You will provide twice as many runners with water as with any of the electrolytes, and you predict that you can study approximately two-thirds as many runners at high altitude than at low altitude. The resulting planned sample size weighting scheme is shown in Table 43.11. Since the scheme is only approximate, you use the NFRACTIONAL option in the POWER statement to disable the rounding of sample sizes up to integers satisfying the weights exactly.
. You will provide twice as many runners with water as with any of the electrolytes, and you predict that you can study approximately two-thirds as many runners at high altitude than at low altitude. The resulting planned sample size weighting scheme is shown in Table 43.11. Since the scheme is only approximate, you use the NFRACTIONAL option in the POWER statement to disable the rounding of sample sizes up to integers satisfying the weights exactly.
Fluid |
|||||
|---|---|---|---|---|---|
Altitude |
Water |
EZD1 |
EZD2 |
LZ1 |
LZ2 |
High |
4 |
2 |
2 |
2 |
2 |
Low |
6 |
3 |
3 |
3 |
3 |
First, you create the exemplary data set to specify means and weights for the design profiles:
data Fluids2;
input Altitude $ Fluid $ LacticAcid CellWgt;
datalines;
High Water 36.9 4
High EZD1 35.0 2
High EZD2 31.5 2
High LZ1 30 2
High LZ2 27.1 2
Low Water 34.3 6
Low EZD1 32.4 3
Low EZD2 28.9 3
Low LZ1 27 3
Low LZ2 24.7 3
;
run;
The variables Altitude, Fluid, and LacticAcid specify the factors and cell means in Table 43.10. The variable CellWgt contains the sample size allocation weights in Table 43.11.
Use the DATA= option in the PROC GLMPOWER statement to specify Fluids2 as the exemplary data set. The following statements perform the sample size analysis:
proc glmpower data=Fluids2;
class Altitude Fluid;
model LacticAcid = Altitude Fluid;
weight CellWgt;
contrast "Water vs. others" Fluid -1 -1 -1 -1 4;
contrast "EZD vs. LZ" Fluid 1 1 -1 -1 0;
contrast "EZD1 vs. EZD2" Fluid 1 -1 0 0 0;
contrast "LZ1 vs. LZ2" Fluid 0 0 1 -1 0;
power
nfractional
stddev = 3.5
ncovariates = 1
corrxy = 0.2 0.3 0
alpha = 0.025
ntotal = .
power = 0.9;
run;
The CLASS statement identifies Altitude and Fluid as classification variables. The MODEL statement specifies the model, and the WEIGHT statement identifies CellWgt as the weight variable. The CONTRAST statement specifies the contrasts in Table 43.9. As in Example 43.1, the order of the contrast coefficients corresponds to the formatted class levels (EZD1, EZD2, LZ1, LZ2, Water). The POWER statement specifies total sample size as the result parameter and provides values for the other analysis parameters. The NCOVARIATES= option specifies the single covariate (body mass index), and the CORRXY= option specifies the two scenarios for its correlation with lactic acid buildup (0.2 and 0.3). Output 43.2.1 displays the results.
| Fixed Scenario Elements | |
|---|---|
| Dependent Variable | LacticAcid |
| Weight Variable | CellWgt |
| Alpha | 0.025 |
| Number of Covariates | 1 |
| Std Dev Without Covariate Adjustment | 3.5 |
| Nominal Power | 0.9 |
| Computed Ceiling N Total | |||||||||
|---|---|---|---|---|---|---|---|---|---|
| Index | Type | Source | Corr XY | Adj Std Dev | Test DF | Error DF | Fractional N Total | Actual Power | Ceiling N Total |
| 1 | Effect | Altitude | 0.2 | 3.43 | 1 | 84 | 90.418451 | 0.902 | 91 |
| 2 | Effect | Altitude | 0.3 | 3.34 | 1 | 79 | 85.862649 | 0.901 | 86 |
| 3 | Effect | Altitude | 0.0 | 3.50 | 1 | 88 | 94.063984 | 0.903 | 95 |
| 4 | Effect | Fluid | 0.2 | 3.43 | 4 | 16 | 22.446173 | 0.912 | 23 |
| 5 | Effect | Fluid | 0.3 | 3.34 | 4 | 15 | 21.687544 | 0.908 | 22 |
| 6 | Effect | Fluid | 0.0 | 3.50 | 4 | 17 | 23.055716 | 0.919 | 24 |
| 7 | Contrast | Water vs. others | 0.2 | 3.43 | 1 | 15 | 21.720195 | 0.905 | 22 |
| 8 | Contrast | Water vs. others | 0.3 | 3.34 | 1 | 14 | 20.848805 | 0.903 | 21 |
| 9 | Contrast | Water vs. others | 0.0 | 3.50 | 1 | 16 | 22.422381 | 0.910 | 23 |
| 10 | Contrast | EZD vs. LZ | 0.2 | 3.43 | 1 | 35 | 41.657424 | 0.903 | 42 |
| 11 | Contrast | EZD vs. LZ | 0.3 | 3.34 | 1 | 33 | 39.674037 | 0.903 | 40 |
| 12 | Contrast | EZD vs. LZ | 0.0 | 3.50 | 1 | 37 | 43.246415 | 0.906 | 44 |
| 13 | Contrast | EZD1 vs. EZD2 | 0.2 | 3.43 | 1 | 139 | 145.613657 | 0.901 | 146 |
| 14 | Contrast | EZD1 vs. EZD2 | 0.3 | 3.34 | 1 | 132 | 138.173983 | 0.902 | 139 |
| 15 | Contrast | EZD1 vs. EZD2 | 0.0 | 3.50 | 1 | 145 | 151.565917 | 0.901 | 152 |
| 16 | Contrast | LZ1 vs. LZ2 | 0.2 | 3.43 | 1 | 268 | 274.055008 | 0.901 | 275 |
| 17 | Contrast | LZ1 vs. LZ2 | 0.3 | 3.34 | 1 | 253 | 259.919126 | 0.900 | 260 |
| 18 | Contrast | LZ1 vs. LZ2 | 0.0 | 3.50 | 1 | 279 | 285.363976 | 0.901 | 286 |
The sample sizes in Output 43.2.1 range from 21 for the comparison of water versus electrolytes (assuming a correlation of 0.3 between body mass and lactic acid buildup) to 275 for the comparison of LZ1 versus LZ2 (assuming a correlation of 0.2). PROC GLMPOWER also includes the effect tests for Altitude and Fluid. Note that the required sample sizes for this study are lower than those for the study in Example 43.1.
Note that the error standard deviation has been reduced from 3.5 to 3.43 (when correlation is 0.2) or 3.34 (when correlation is 0.3) in the approximation of the effect of the body mass index covariate. The error degrees of freedom has also been automatically adjusted, lowered by 1 (the number of covariates).
Suppose you want to plot the required sample size for the range of power values from 0.5 to 0.95. First, define the analysis by specifying the same statements as before, but add the PLOTONLY option to the PROC GLMPOWER statement to disable the nongraphical results. Next, specify the PLOT statement with X=POWER to request a plot with power on the X axis. Sample size is automatically placed on the Y axis. Use the MIN= and MAX= options in the PLOT statement to specify the power range. The following statements produce the plot:
ods listing style=htmlbluecml;
ods graphics on;
proc glmpower data=Fluids2 plotonly;
class Altitude Fluid;
model LacticAcid = Altitude Fluid;
weight CellWgt;
contrast "Water vs. others" Fluid -1 -1 -1 -1 4;
contrast "EZD vs. LZ" Fluid 1 1 -1 -1 0;
contrast "EZD1 vs. EZD2" Fluid 1 -1 0 0 0;
contrast "LZ1 vs. LZ2" Fluid 0 0 1 -1 0;
power
nfractional
stddev = 3.5
ncovariates = 1
corrxy = 0.2 0.3 0
alpha = 0.025
ntotal = .
power = 0.9;
plot x=power min=.5 max=.95;
run;
The ODS LISTING STYLE=HTMLBLUECML statement specifies the HTMLBLUECML style, which is suitable for use with PROC GLMPOWER because it allows both marker symbols and line styles to vary. See the section ODS Styles Suitable for Use with PROC GLMPOWER for more information. See Output 43.2.2 for the resulting plot.

In Output 43.1.2, the line style identifies the test, and the plotting symbol identifies the scenario for the correlation between covariate and response. The plotting symbol locations identify actual computed powers; the curves are linear interpolations of these points. As in Example 43.1, the required sample size is highest for the test of LZ1 versus LZ2.
Finally, suppose you want to plot the power for the range of sample sizes you will likely consider for the study (the range of 21 to 275 that achieves 0.9 power for different comparisons). In the POWER statement, identify power as the result (POWER=.), and specify NTOTAL=21. Specify the PLOT statement with X=N to request a plot with sample size on the X axis.
The following statements produce the plot:
proc glmpower data=Fluids2 plotonly;
class Altitude Fluid;
model LacticAcid = Altitude Fluid;
weight CellWgt;
contrast "Water vs. others" Fluid -1 -1 -1 -1 4;
contrast "EZD vs. LZ" Fluid 1 1 -1 -1 0;
contrast "EZD1 vs. EZD2" Fluid 1 -1 0 0 0;
contrast "LZ1 vs. LZ2" Fluid 0 0 1 -1 0;
power
nfractional
stddev = 3.5
ncovariates = 1
corrxy = 0.2 0.3 0
alpha = 0.025
ntotal = 21
power = .;
plot x=n min=21 max=275;
run;
ods graphics off;
The MAX=275 option in the PLOT statement sets the maximum sample size value. The MIN= option automatically defaults to the value of 21 from the NTOTAL= option in the POWER statement.
See Output 43.2.3 for the plot.

Although Output 43.2.2 and Output 43.2.3 surface essentially the same computations for practical power ranges, they each provide a different quick visual assessment. Output 43.2.2 reveals the range of required sample sizes for powers of interest, and Output 43.2.3 reveals the range of powers achieved for sample sizes of interest.
