The DISTANCE Procedure
| PROC DISTANCE Statement |
- PROC DISTANCE <options> ;
The options available with the PROC DISTANCE statement are summarized in Table 33.1 and discussed in the following section.
Option |
Description |
|---|---|
Standardize variables |
|
Specifies the constant to add to each value after standardizing and multiplying by the value specified in the MULT= option |
|
Specifies the relative fuzz factor for writing the output |
|
Specifies the method for computing initial estimates for the A-estimates |
|
Specifies the constant to multiply each value by after standardizing |
|
Normalizes the scale estimator to be consistent for the standard deviation of a normal distribution |
|
Suppresses standardization |
|
Normalizes the scale estimator to have an expectation of approximately 1 for a standard normal distribution |
|
Standardizes variables only (suppresses computation of the distance matrix) |
|
Specifies the variances divisor |
|
Generate distance matrix |
|
Specifies the value to be used as an absence value for all the asymmetric nominal variables |
|
Specifies the method for computing proximity measures |
|
Specifies a prefix for naming the distance variables in the OUT= data set |
|
Specifies the method of assigning scores to ordinal variables |
|
Specifies the shape of the proximity matrix to be stored in the OUT= data set |
|
Specifies the numeric constant used to replace undefined distances |
|
Replace missing values |
|
Omits observations with missing values from computation of the location and scale measures, if standardization applies; outputs missing values to the distance matrix for observations with missing values |
|
Replaces missing data with zero in the standardized data |
|
Replaces missing data with the location measure (does not standardize the data) |
|
Specify data set details |
|
Specifies the input data set |
|
Specifies the output data set |
|
Specifies the output data set for standardized scores |
|
These options and their abbreviations are described (in alphabetical order) in the remainder of this section.
- ABSENT=number | qs
-
specifies the value to be used as an absence value in an irrelevant absent-absent match for all of the asymmetric nominal variables. If you want to specify a different absence value for a particular variable, use the ABSENT= option in the VAR statement. See the ABSENT= option in the section VAR Statement for details.
An absence value for a variable can be either a numeric value or a quoted string consisting of combinations of characters. For instance, ., -999, and "NA" are legal values for the ABSENT= option.
The default absence value for a character variable is "NONE" (notice that a blank value is considered a missing value), and the default absence value for a numeric variable is 0.
- ADD=c
specifies a constant, c, to add to each value after standardizing and multiplying by the value you specify in the MULT= option. The default value is 0.
- DATA=SAS-data-set
specifies the input data set containing observations from which the proximity is computed. If you omit the DATA= option, the most recently created SAS data set is used.
- FUZZ=c
-
specifies the relative fuzz factor for computing the standardized scores. The default value is 1E–14. For the OUTSDZ= data set, the score is computed as follows:
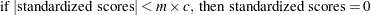
where m is the numeric constant specified in the MULT= option, or 1 if MULT= option is not specified.
- INITIAL=method
-
specifies the method of computing initial estimates for the A-estimates (ABW, AWAVE, and AHUBER). The following methods are not allowed for the INITIAL= option: ABW, AHUBER, AWAVE, and IN.
The default value is INITIAL=MAD.
- METHOD=method
-
specifies the method of computing proximity measures.
For use in PROC CLUSTER, distance or dissimilarity measures such as METHOD=EUCLID or METHOD=DGOWER should be chosen.
The following six tables outline the proximity measures available for the METHOD= option. These tables are classified by levels of measurement accepted by each method. Each table contains four or five columns: the Method column shows the proximity measures, one or two Range columns show the upper and lower bounds, and the TYPE= column shows the type of proximity. The TYPE= column contains SIMILAR if a method generates similarity measures or DISTANCE if a method generates distance or dissimilarity measures. The output data set is of the type shown. For more information about the output data set, see the OUT= option.
For formulas and descriptions of these methods, see the section Details: DISTANCE Procedure.
Table 33.2 shows the range and output matrix type of the GOWER and DGOWER methods. These two methods accept all measurement levels including ratio, interval, ordinal, nominal, and asymmetric nominal. METHOD=GOWER or METHOD=DGOWER always implies standardization. Assuming all the numeric (ordinal, interval, and ratio) variables are standardized by their corresponding default methods, the possible range values for both methods are from 0 and 1, inclusive. For more information about the default methods of standardization for METHOD=GOWER or METHOD=DGOWER, see the STD= option in the section VAR Statement.
Table 33.2 Methods That Accept All Measurement Levels Method
Description
Range
TYPE=
GOWER
Gower and Legendre (1986) similarity
0 to 1
SIMILAR
DGOWER
1 minus GOWER
0 to 1
DISTANCE
Table 33.3 shows methods that accept ratio, interval, and ordinal variables.
Table 33.3 Methods That Accept Ratio, Interval, and Ordinal Variables Method
Description
Range
TYPE=
EUCLID
Euclidean distance
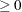
DISTANCE
SQEUCLID
Squared Euclidean distance
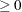
DISTANCE
SIZE
Size distance
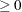
DISTANCE
SHAPE
Shape distance
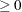
DISTANCE
COV
Covariance
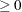
SIMILAR
CORR
Correlation
–1 to 1
SIMILAR
DCORR
Correlation transformed to Euclidean distance
0 to 2
DISTANCE
SQCORR
Squared correlation
0 to 1
SIMILAR
DSQCORR
One minus squared correlation
0 to 1
DISTANCE
L(p)
Minkowski (
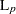 ) distance, where p is a positive numeric value
) distance, where p is a positive numeric value 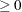
DISTANCE
CITYBLOCK
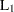 , city-block, or Manhattan distance
, city-block, or Manhattan distance 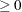
DISTANCE
CHEBYCHEV
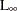
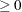
DISTANCE
POWER(
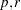 )
)Generalized Euclidean distance where p is a positive numeric value and r is a nonnegative numeric value. The distance between two observations is the rth root of sum of the absolute differences to the pth power between the values for the observations.
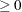
DISTANCE
Table 33.4 shows methods that accept ratio variables. Notice that all possible range values are nonnegative, because ratio variables are assumed to be positive.
Table 33.4 Methods That Accept Ratio Variables Method
Description
Range
TYPE=
SIMRATIO
Similarity ratio (if variables are binary, this is the Jaccard coefficient)
0 to 1
SIMILAR
DISRATIO
One minus similarity ratio
0 to 1
DISTANCE
NONMETRIC
Lance and Williams nonmetric coefficient
0 to 1
DISTANCE
CANBERRA
Canberra metric distance coefficient
0 to 1
DISTANCE
COSINE
Cosine coefficient
0 to 1
SIMILAR
DOT
Dot (inner) product coefficient
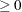
SIMILAR
OVERLAP
Overlap similarity
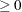
SIMILAR
DOVERLAP
Overlap dissimilarity
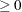
DISTANCE
CHISQ
Chi-squared coefficient
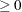
DISTANCE
CHI
Squared root of chi-squared coefficient
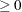
DISTANCE
PHISQ
Phi-squared coefficient
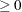
DISTANCE
PHI
Squared root of phi-squared coefficient
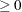
DISTANCE
Table 33.5 shows methods that accept nominal variables.
Table 33.5 Methods That Accept Nominal Variables Method
Description
Range
TYPE=
HAMMING
Hamming distance
0 to v
DISTANCE
MATCH
Simple matching coefficient
0 to 1
SIMILAR
DMATCH
Simple matching coefficient transformed to Euclidean distance
0 to 1
DISTANCE
DSQMATCH
Simple matching coefficient transformed to squared Euclidean distance
0 to 1
DISTANCE
HAMANN
Hamann coefficient
–1 to 1
SIMILAR
RT
Roger and Tanimoto
0 to 1
SIMILAR
SS1
Sokal and Sneath 1
0 to 1
SIMILAR
SS3
Sokal and Sneath 3
0 to 1
SIMILAR
Note that v denotes the number of variables (dimensionality).
Table 33.6 shows methods that accept asymmetric nominal variables. Use the ABSENT= option to create a value to be considered absent.
Table 33.6 Methods That Accept Asymmetric Nominal Variables Method
Description
Range
TYPE=
DICE
Dice coefficient or Czekanowski/Sorensen similarity coefficient
0 to 1
SIMILAR
RR
Russell and Rao
0 to 1
SIMILAR
BLWNM
Binary Lance and Williams nonmetric, or Bray-Curtis coefficient
0 to 1
DISTANCE
K1
Kulcynski 1
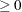
SIMILAR
Table 33.7 shows methods that accept asymmetric nominal and ratio variables. Use the ABSENT= option to create a value to be considered absent. The table contains five columns. The third column contains possible range values if only one level of measurement (either ratio or asymmetric nominal but not both) is specified; the fourth column contains possible range values if both levels are specified.
The JACCARD method is equivalent to the SIMRATIO method if there is no asymmetric nominal variable; if both ratio and asymmetric nominal variables are present, the coefficient is computed as the sum of the coefficient from the ratio variables and the coefficient from the asymmetric nominal variables. See "Proximity Measures" in the section Details: DISTANCE Procedure for the formula and descriptions of the JACCARD method.
Table 33.7 Methods That Accept Asymmetric Nominal and Ratio Variables Method
Description
Range (One Level)
Range (Two Levels)
TYPE=
JACCARD
Jaccard similarity
coefficient0 to 1
0 to 2
SIMILAR
DJACCARD
Jaccard dissimilarity
coefficient0 to 1
0 to 2
DISTANCE
- MULT=c
specifies a numeric constant, c, by which to multiply each value after standardizing. The default value is 1.
- NOMISS
-
omits observations with missing values from computation of the location and scale measures when standardizing; generates undefined (missing) distances for observations with missing values when computing distances. Use the UNDEF= option to specify the undefined values.
If a distance matrix is created to be used as an input to PROC CLUSTER, the NOMISS option should not be used because PROC CLUSTER does not accept distance matrices with missing values.
- NORM
normalizes the scale estimator to be consistent for the standard deviation of a normal distribution when you specify the option STD=AGK, STD=IQR, STD=MAD, or STD=SPACING in the VAR statement.
- NOSTD
suppresses standardization of the variables. The NOSTD option should not be specified with the STDONLY option or with the REPLACE option.
- OUT=SAS-data-set
-
specifies the name of the SAS data set created by PROC DISTANCE. The output data set contains the BY variables, the ID variable, computed distance variables, the COPY variables, the FREQ variable, and the WEIGHT variables.
If you omit the OUT= option, PROC DISTANCE creates an output data set named according to the DATAn convention.
The output data set is of type TYPE=DISTANCE or TYPE=SIMILAR. See the METHOD= option for more information about the association between the method and the output data set type. Data set types do not persist when you copy or modify a data set. You must specify the TYPE= data set option for the new data set, as in the following example:
data dist2(type=distance); set dist; run;
If you do not specify the TYPE=DISTANCE data set option, the new data set is the default TYPE=DATA. If you use the new data set in a procedure that accepts both TYPE=DATA or TYPE=DISTANCE data sets (such as PROC CLUSTER or PROC MODECLUS), the results will be incorrect.
- OUTSDZ=SAS-data-set
specifies the name of the SAS data set containing the standardized scores. The output data set contains a copy of the DATA= data set, except that the analyzed variables have been standardized. Analyzed variables are those listed in the VAR statement.
- PREFIX=name
-
specifies a prefix for naming the distance variables in the OUT= data set. By default, the names are Dist1, Dist2, ..., Distn. If you specify PREFIX=ABC, the variables are named ABC1, ABC2, ..., ABCn. If the ID statement is also specified, the variables are named by appending the value of the ID variable to the prefix.
- RANKSCORE=MIDRANK | INDEX
-
specifies the method of assigning scores to ordinal variables. The available methods are listed as follows:
- MIDRANK
assigns consecutive integers to each category with consideration of the frequency value. This is the default method.
- INDEX
assigns consecutive integers to each category regardless of frequencies.
The following example explains how each method assigns the rank scores. Suppose the data contain an ordinal variable ABC with values A, B, C. There are two ways to assign numbers. One is to use midranks, which depend on the frequencies of each category. Another is to assign consecutive integers to each category, regardless of frequencies.
Table 33.8 Example of Assigning Rank Scores ABC
MIDRANK
INDEX
A
1.5
1
A
1.5
1
B
4
2
B
4
2
B
4
2
C
6
3
- REPLACE
-
replaces missing data with zero in the standardized data (to correspond to the location measure before standardizing). To replace missing data with something else, use the MISSING= option in the VAR statement. The REPLACE option implies standardization.
You cannot specify the following options together:
both the REPLACE and the REPONLY options
both the REPLACE and the NOSTD options
- REPONLY
-
replaces missing data with the location measure specified by the MISSING= option or the STD= option (if the MISSING= option is not specified), but does not standardize the data. If the MISSING= option is not specified and METHOD=GOWER is specified, missing values are replaced by the location measure from the RANGE method (the minimum value), no matter what the value of the STD= option is.
You cannot specify both the REPLACE and the REPONLY options.
- SHAPE=TRIANGLE | TRI | SQUARE | SQU | SQR
specifies the shape of the proximity matrix to be stored in the OUT= data set. SHAPE=TRIANGLE requests the matrix to be stored as a lower triangular matrix; SHAPE=SQUARE requests that the matrix be stored as a squared matrix. Use SHAPE=SQUARE if the output data set is to be used as input to the MODECLUS procedures. The default is TRIANGLE.
- SNORM
-
normalizes the scale estimator to have an expectation of approximately 1 for a standard normal distribution when the STD=SPACING option is specified.
- STDONLY
standardizes variables only and computes no distance matrix. You must use the OUTSDZ= option to save the standardized scores. You cannot specify both the STDONLY option and the NOSTD option.
- UNDEF=n
-
specifies the numeric constant used to replace undefined distances, such as when an observation has all missing values, or if a divisor is zero.
- VARDEF=DF | N | WDF | WEIGHT | WGT
-
specifies the divisor to be used in the calculation of distance, dissimilarity, or similarity measures, and for standardizing variables whenever a variance or covariance is computed. By default, VARDEF=DF. The values and associated divisors are as follows:
Value
Divisor
Formula
DF
degrees of freedom

N
number of observations
n
WDF
sum of weights minus 1
(
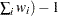
WEIGHT | WGT
sum of weights