The CANCORR Procedure
Example 27.1 Canonical Correlation Analysis of Fitness Club Data
Three physiological and three exercise variables are measured on 20 middle-aged men in a fitness club. You can use the CANCORR procedure to determine whether the physiological variables are related in any way to the exercise variables. The following statements create the SAS data set Fit and produce Output 27.1.1 through Output 27.1.5:
data Fit; input Weight Waist Pulse Chins Situps Jumps; datalines; 191 36 50 5 162 60 189 37 52 2 110 60 193 38 58 12 101 101 162 35 62 12 105 37 189 35 46 13 155 58 182 36 56 4 101 42 211 38 56 8 101 38 167 34 60 6 125 40 176 31 74 15 200 40 154 33 56 17 251 250 169 34 50 17 120 38 166 33 52 13 210 115 154 34 64 14 215 105 247 46 50 1 50 50 193 36 46 6 70 31 202 37 62 12 210 120 176 37 54 4 60 25 157 32 52 11 230 80 156 33 54 15 225 73 138 33 68 2 110 43 ;
proc cancorr data=Fit all
vprefix=Physiological vname='Physiological Measurements'
wprefix=Exercises wname='Exercises';
var Weight Waist Pulse;
with Chins Situps Jumps;
title 'Middle-Aged Men in a Health Fitness Club';
title2 'Data Courtesy of Dr. A. C. Linnerud, NC State Univ';
run;
| Middle-Aged Men in a Health Fitness Club |
| Data Courtesy of Dr. A. C. Linnerud, NC State Univ |
| Correlations Among the Physiological Measurements | |||
|---|---|---|---|
| Weight | Waist | Pulse | |
| Weight | 1.0000 | 0.8702 | -0.3658 |
| Waist | 0.8702 | 1.0000 | -0.3529 |
| Pulse | -0.3658 | -0.3529 | 1.0000 |
| Correlations Among the Exercises | |||
|---|---|---|---|
| Chins | Situps | Jumps | |
| Chins | 1.0000 | 0.6957 | 0.4958 |
| Situps | 0.6957 | 1.0000 | 0.6692 |
| Jumps | 0.4958 | 0.6692 | 1.0000 |
| Correlations Between the Physiological Measurements and the Exercises | |||
|---|---|---|---|
| Chins | Situps | Jumps | |
| Weight | -0.3897 | -0.4931 | -0.2263 |
| Waist | -0.5522 | -0.6456 | -0.1915 |
| Pulse | 0.1506 | 0.2250 | 0.0349 |
Output 27.1.1 displays the correlations among the original variables. The correlations between the physiological and exercise variables are moderate, the largest being 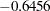 between Waist and Situps. There are larger within-set correlations: 0.8702 between Weight and Waist, 0.6957 between Chins and Situps, and 0.6692 between Situps and Jumps.
between Waist and Situps. There are larger within-set correlations: 0.8702 between Weight and Waist, 0.6957 between Chins and Situps, and 0.6692 between Situps and Jumps.
| Middle-Aged Men in a Health Fitness Club |
| Data Courtesy of Dr. A. C. Linnerud, NC State Univ |
| Canonical Correlation |
Adjusted Canonical Correlation |
Approximate Standard Error |
Squared Canonical Correlation |
Eigenvalues of Inv(E)*H = CanRsq/(1-CanRsq) |
Test of H0: The canonical correlations in the current row and all that follow are zero | ||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Eigenvalue | Difference | Proportion | Cumulative | Likelihood Ratio |
Approximate F Value |
Num DF | Den DF | Pr > F | |||||
| 1 | 0.795608 | 0.754056 | 0.084197 | 0.632992 | 1.7247 | 1.6828 | 0.9734 | 0.9734 | 0.35039053 | 2.05 | 9 | 34.223 | 0.0635 |
| 2 | 0.200556 | -.076399 | 0.220188 | 0.040223 | 0.0419 | 0.0366 | 0.0237 | 0.9970 | 0.95472266 | 0.18 | 4 | 30 | 0.9491 |
| 3 | 0.072570 | . | 0.228208 | 0.005266 | 0.0053 | 0.0030 | 1.0000 | 0.99473355 | 0.08 | 1 | 16 | 0.7748 | |
| Multivariate Statistics and F Approximations | |||||
|---|---|---|---|---|---|
| S=3 M=-0.5 N=6 | |||||
| Statistic | Value | F Value | Num DF | Den DF | Pr > F |
| Wilks' Lambda | 0.35039053 | 2.05 | 9 | 34.223 | 0.0635 |
| Pillai's Trace | 0.67848151 | 1.56 | 9 | 48 | 0.1551 |
| Hotelling-Lawley Trace | 1.77194146 | 2.64 | 9 | 19.053 | 0.0357 |
| Roy's Greatest Root | 1.72473874 | 9.20 | 3 | 16 | 0.0009 |
| NOTE: F Statistic for Roy's Greatest Root is an upper bound. | |||||
As Output 27.1.2 shows, the first canonical correlation is 0.7956, which would appear to be substantially larger than any of the between-set correlations. The probability level for the null hypothesis that all the canonical correlations are zero in the population is only 0.0635, so no firm conclusions can be drawn. The remaining canonical correlations are not worthy of consideration, as can be seen from the probability levels and especially from the negative adjusted canonical correlations.
Because the variables are not measured in the same units, the standardized coefficients rather than the raw coefficients should be interpreted. The correlations given in the canonical structure matrices should also be examined.
| Raw Canonical Coefficients for the Physiological Measurements | |||
|---|---|---|---|
| Physiological1 | Physiological2 | Physiological3 | |
| Weight | -0.031404688 | -0.076319506 | -0.007735047 |
| Waist | 0.4932416756 | 0.3687229894 | 0.1580336471 |
| Pulse | -0.008199315 | -0.032051994 | 0.1457322421 |
| Raw Canonical Coefficients for the Exercises | |||
|---|---|---|---|
| Exercises1 | Exercises2 | Exercises3 | |
| Chins | -0.066113986 | -0.071041211 | -0.245275347 |
| Situps | -0.016846231 | 0.0019737454 | 0.0197676373 |
| Jumps | 0.0139715689 | 0.0207141063 | -0.008167472 |
| Standardized Canonical Coefficients for the Physiological Measurements |
|||
|---|---|---|---|
| Physiological1 | Physiological2 | Physiological3 | |
| Weight | -0.7754 | -1.8844 | -0.1910 |
| Waist | 1.5793 | 1.1806 | 0.5060 |
| Pulse | -0.0591 | -0.2311 | 1.0508 |
| Standardized Canonical Coefficients for the Exercises |
|||
|---|---|---|---|
| Exercises1 | Exercises2 | Exercises3 | |
| Chins | -0.3495 | -0.3755 | -1.2966 |
| Situps | -1.0540 | 0.1235 | 1.2368 |
| Jumps | 0.7164 | 1.0622 | -0.4188 |
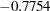 ), with more emphasis on Waist. The coefficient for Pulse is near 0. The correlations between Waist and Weight and the first canonical variable are both positive, 0.9254 for Waist and 0.6206 for Weight. Weight is therefore a suppressor variable, meaning that its coefficient and its correlation have opposite signs.
), with more emphasis on Waist. The coefficient for Pulse is near 0. The correlations between Waist and Weight and the first canonical variable are both positive, 0.9254 for Waist and 0.6206 for Weight. Weight is therefore a suppressor variable, meaning that its coefficient and its correlation have opposite signs. The first canonical variable for the exercise variables also shows a mixture of signs, subtracting Situps ( ) and Chins (
) and Chins (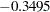 ) from Jumps (0.7164), with the most weight on Situps. All the correlations are negative, indicating that Jumps is also a suppressor variable.
) from Jumps (0.7164), with the most weight on Situps. All the correlations are negative, indicating that Jumps is also a suppressor variable.
It might seem contradictory that a variable should have a coefficient of opposite sign from that of its correlation with the canonical variable. In order to understand how this can happen, consider a simplified situation: predicting Situps from Waist and Weight by multiple regression. In informal terms, it seems plausible that obese people should do fewer sit-ups than skinny people. Assume that the men in the sample do not vary much in height, so there is a strong correlation between Waist and Weight (0.8702). Examine the relationships between obesity and the independent variables:
People with large waists tend to be more obese than people with small waists. Hence, the correlation between Waist and Situps should be negative.
People with high weights tend to be more obese than people with low weights. Therefore, Weight should correlate negatively with Situps.
For a fixed value of Weight, people with large waists tend to be shorter and more obese. Thus, the multiple regression coefficient for Waist should be negative.
For a fixed value of Waist, people with higher weights tend to be taller and skinnier. The multiple regression coefficient for Weight should therefore be positive, of opposite sign from the correlation between Weight and Situps.
Therefore, the general interpretation of the first canonical correlation is that Weight and Jumps act as suppressor variables to enhance the correlation between Waist and Situps. This canonical correlation might be strong enough to be of practical interest, but the sample size is not large enough to draw definite conclusions.
The canonical redundancy analysis (Output 27.1.4) shows that neither of the first pair of canonical variables is a good overall predictor of the opposite set of variables, the proportions of variance explained being 0.2854 and 0.2584. The second and third canonical variables add virtually nothing, with cumulative proportions for all three canonical variables being 0.2969 and 0.2767.
| Middle-Aged Men in a Health Fitness Club |
| Data Courtesy of Dr. A. C. Linnerud, NC State Univ |
| Standardized Variance of the Physiological Measurements Explained by | |||||
|---|---|---|---|---|---|
| Canonical Variable Number |
Their Own Canonical Variables |
Canonical R-Square |
The Opposite Canonical Variables |
||
| Proportion | Cumulative Proportion |
Proportion | Cumulative Proportion |
||
| 1 | 0.4508 | 0.4508 | 0.6330 | 0.2854 | 0.2854 |
| 2 | 0.2470 | 0.6978 | 0.0402 | 0.0099 | 0.2953 |
| 3 | 0.3022 | 1.0000 | 0.0053 | 0.0016 | 0.2969 |
| Standardized Variance of the Exercises Explained by | |||||
|---|---|---|---|---|---|
| Canonical Variable Number |
Their Own Canonical Variables |
Canonical R-Square |
The Opposite Canonical Variables |
||
| Proportion | Cumulative Proportion |
Proportion | Cumulative Proportion |
||
| 1 | 0.4081 | 0.4081 | 0.6330 | 0.2584 | 0.2584 |
| 2 | 0.4345 | 0.8426 | 0.0402 | 0.0175 | 0.2758 |
| 3 | 0.1574 | 1.0000 | 0.0053 | 0.0008 | 0.2767 |
The squared multiple correlations (Output 27.1.5) indicate that the first canonical variable of the physiological measurements has some predictive power for Chins (0.3351) and Situps (0.4233) but almost none for Jumps (0.0167). The first canonical variable of the exercises is a fairly good predictor of Waist (0.5421), a poorer predictor of Weight (0.2438), and nearly useless for predicting Pulse (0.0701).
| Squared Multiple Correlations Between the Physiological Measurements and the First M Canonical Variables of the Exercises | |||
|---|---|---|---|
| M | 1 | 2 | 3 |
| Weight | 0.2438 | 0.2678 | 0.2679 |
| Waist | 0.5421 | 0.5478 | 0.5478 |
| Pulse | 0.0701 | 0.0702 | 0.0749 |
| Squared Multiple Correlations Between the Exercises and the First M Canonical Variables of the Physiological Measurements | |||
|---|---|---|---|
| M | 1 | 2 | 3 |
| Chins | 0.3351 | 0.3374 | 0.3396 |
| Situps | 0.4233 | 0.4365 | 0.4365 |
| Jumps | 0.0167 | 0.0536 | 0.0539 |
