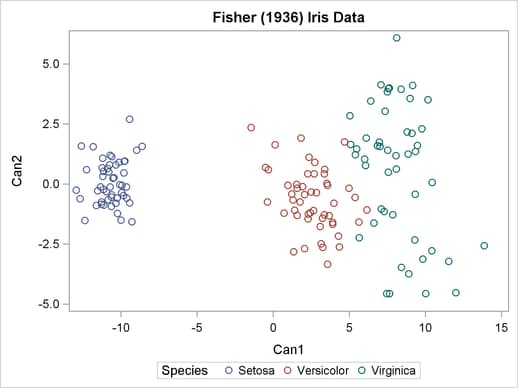
Example 23.1 Transformation and Cluster Analysis of Fisher Iris Data
The iris data published by Fisher (1936) have been widely used for examples in discriminant analysis and cluster analysis. The sepal length, sepal width, petal length, and petal width are measured in millimeters on 50 iris specimens from each of three species, Iris setosa, I. versicolor, and I. virginica. Mezzich and Solomon (1980) discuss a variety of cluster analyses of the iris data.
In this example PROC ACECLUS is used to transform the iris data, which is available from the Sashelp library, and the clustering is performed by PROC FASTCLUS. Compare this with the example in
Chapter 35,
The FASTCLUS Procedure.
The results from the FREQ procedure display fewer misclassifications when PROC ACECLUS is used.
The following statements produce Output 23.1.1 through Output 23.1.5:
title 'Fisher (1936) Iris Data';
proc aceclus data=sashelp.iris out=ace p=.02 outstat=score;
var SepalLength SepalWidth PetalLength PetalWidth ;
run;
proc sgplot data=ace;
scatter y=can2 x=can1 / group=Species;
keylegend / title="Species";
run;
proc fastclus data=ace maxc=3 maxiter=10 conv=0 out=clus;
var can:;
run;
proc freq;
tables cluster*Species;
run;
Output 23.1.1
Using PROC ACECLUS to Transform Fisher’s Iris Data
The ACECLUS Procedure
Approximate Covariance Estimation for Cluster Analysis
| 58.4333 |
8.2807 |
Sepal Length (mm) |
| 30.5733 |
4.3587 |
Sepal Width (mm) |
| 37.5800 |
17.6530 |
Petal Length (mm) |
| 11.9933 |
7.6224 |
Petal Width (mm) |
| 68.5693512 |
-4.2434004 |
127.4315436 |
51.6270694 |
| -4.2434004 |
18.9979418 |
-32.9656376 |
-12.1639374 |
| 127.4315436 |
-32.9656376 |
311.6277852 |
129.5609396 |
| 51.6270694 |
-12.1639374 |
129.5609396 |
58.1006264 |
Initial Within-Cluster Covariance Estimate = Full Covariance Matrix
| 2.828 |
0.945 |
408.0 |
0.465775 |
| 11.905 |
3.979 |
559.0 |
0.013487 |
| 13.152 |
4.396 |
940.0 |
0.029499 |
| 13.439 |
4.491 |
1506.0 |
0.046846 |
| 13.271 |
4.435 |
2036.0 |
0.046859 |
| 12.591 |
4.208 |
2285.0 |
0.025027 |
| 12.199 |
4.077 |
2366.0 |
0.009559 |
| 12.121 |
4.051 |
2402.0 |
0.003895 |
| 12.064 |
4.032 |
2417.0 |
0.002051 |
| 12.047 |
4.026 |
2429.0 |
0.000971 |
Output 23.1.2
Eigenvalues, Raw Canonical Coefficients, and Standardized Canonical Coefficients
| 11.73342939 |
5.47550432 |
4.95389049 |
2.02902429 |
| 5.47550432 |
6.91992590 |
2.42177851 |
1.74125154 |
| 4.95389049 |
2.42177851 |
6.53746398 |
2.35302594 |
| 2.02902429 |
1.74125154 |
2.35302594 |
2.05166735 |
| 63.7716 |
61.1593 |
0.9367 |
0.9367 |
| 2.6123 |
1.5561 |
0.0384 |
0.9751 |
| 1.0562 |
0.4167 |
0.0155 |
0.9906 |
| 0.6395 |
|
0.00939 |
1.0000 |
| Sepal Length (mm) |
-.012009 |
-.098074 |
-.059852 |
0.402352 |
| Sepal Width (mm) |
-.211068 |
-.000072 |
0.402391 |
-.225993 |
| Petal Length (mm) |
0.324705 |
-.328583 |
0.110383 |
-.321069 |
| Petal Width (mm) |
0.266239 |
0.870434 |
-.085215 |
0.320286 |
| Sepal Length (mm) |
-0.09944 |
-0.81211 |
-0.49562 |
3.33174 |
| Sepal Width (mm) |
-0.91998 |
-0.00031 |
1.75389 |
-0.98503 |
| Petal Length (mm) |
5.73200 |
-5.80047 |
1.94859 |
-5.66782 |
| Petal Width (mm) |
2.02937 |
6.63478 |
-0.64954 |
2.44134 |
Output 23.1.3
Plot of Transformed Iris Data: PROC SGPLOT
Output 23.1.4
Clustering of Transformed Iris Data: Partial Output from PROC FASTCLUS
The FASTCLUS Procedure
Replace=FULL Radius=0 Maxclusters=3 Maxiter=10 Converge=0
| 50 |
1.4138 |
5.3152 |
|
2 |
5.8580 |
| 50 |
1.8880 |
6.8298 |
|
1 |
5.8580 |
| 50 |
1.1016 |
5.2768 |
|
1 |
13.2845 |
| 8.04808 |
1.48537 |
0.966394 |
28.756658 |
| 1.90061 |
1.85646 |
0.058725 |
0.062389 |
| 1.43395 |
1.32518 |
0.157417 |
0.186826 |
| 1.28044 |
1.27550 |
0.021025 |
0.021477 |
| 4.24499 |
1.50298 |
0.876324 |
7.085666 |
WARNING: The two values above are invalid for correlated variables.
| 2.54528754 |
-0.59273569 |
-0.78905317 |
-0.26079612 |
| 8.12988211 |
0.52566663 |
0.51836499 |
0.14915404 |
| -10.67516964 |
0.06706906 |
0.27068819 |
0.11164209 |
| 1.572366584 |
1.393565864 |
1.303411851 |
1.372050319 |
| 1.799159552 |
2.743869556 |
1.270344142 |
1.370523175 |
| 0.953761025 |
0.931943571 |
1.398456061 |
1.058217627 |
Output 23.1.5
Crosstabulation of Cluster by Species for Fisher’s Iris Data: PROC FREQ
Copyright © SAS Institute Inc. All rights reserved.