Example 91.3 Penalized B-Spline

The following data set contains measurements of monthly averaged atmospheric pressure differences between Easter Island and Darwin, Australia, for a period of 168 months (National Institute of Standards and Technology; 1998):

title 'Atmospheric Pressure Changes Between'
      ' Easter Island & Darwin, Australia';

data ENSO;
   input Pressure @@;
   Year = _n_ / 12;
   datalines;
12.9  11.3  10.6  11.2  10.9   7.5   7.7  11.7
12.9  14.3  10.9  13.7  17.1  14.0  15.3   8.5
 5.7   5.5   7.6   8.6   7.3   7.6  12.7  11.0
12.7  12.9  13.0  10.9  10.4  10.2   8.0  10.9
13.6  10.5   9.2  12.4  12.7  13.3  10.1   7.8
 4.8   3.0   2.5   6.3   9.7  11.6   8.6  12.4
10.5  13.3  10.4   8.1   3.7  10.7   5.1  10.4
10.9  11.7  11.4  13.7  14.1  14.0  12.5   6.3
 9.6  11.7   5.0  10.8  12.7  10.8  11.8  12.6
15.7  12.6  14.8   7.8   7.1  11.2   8.1   6.4
 5.2  12.0  10.2  12.7  10.2  14.7  12.2   7.1
 5.7   6.7   3.9   8.5   8.3  10.8  16.7  12.6
12.5  12.5   9.8   7.2   4.1  10.6  10.1  10.1
11.9  13.6  16.3  17.6  15.5  16.0  15.2  11.2
14.3  14.5   8.5  12.0  12.7  11.3  14.5  15.1
10.4  11.5  13.4   7.5   0.6   0.3   5.5   5.0
 4.6   8.2   9.9   9.2  12.5  10.9   9.9   8.9
 7.6   9.5   8.4  10.7  13.6  13.7  13.7  16.5
16.8  17.1  15.4   9.5   6.1  10.1   9.3   5.3
11.2  16.6  15.6  12.0  11.5   8.6  13.8   8.7
 8.6   8.6   8.7  12.8  13.2  14.0  13.4  14.8
;

You can fit a curve through these data by using a penalized B-spline (Eilers and Marx; 1996) function and the following statements:

ods graphics on;

proc transreg data=enso;
   model identity(pressure) = pbspline(year);
run;

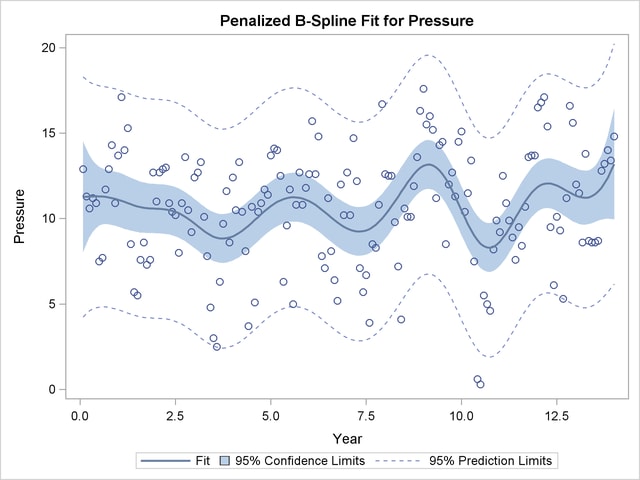
The dependent variable Pressure is specified along with an IDENTITY transformation, so Pressure is analyzed as is, with no transformations. The independent variable Year is specified with a PBSPLINE transformation, so a penalized B-spline model is fit. By default, a DEGREE=3 B-spline basis is used along with 100 evenly spaced knots and three evenly spaced exterior knots on each side of the data. The penalized spline function is typically much smoother than you would get by using a SPLINE transformation or a BSPLINE expansion since changes in the coefficients of the basis are penalized to make a smoother fit. The output is shown next in Output 91.3.1.

Output 91.3.1 Change in Atmospheric Pressure, AICC

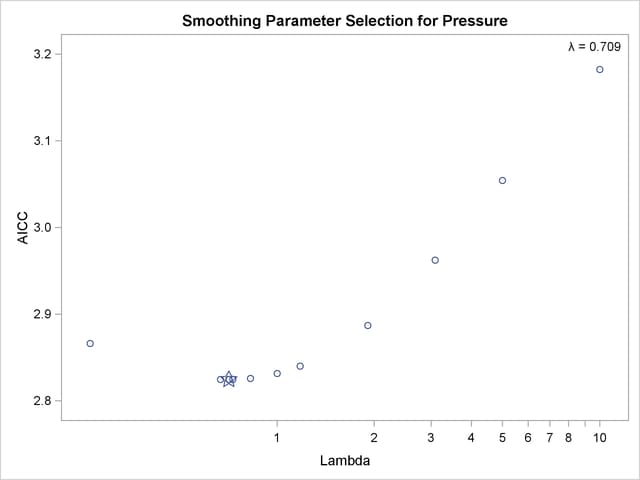
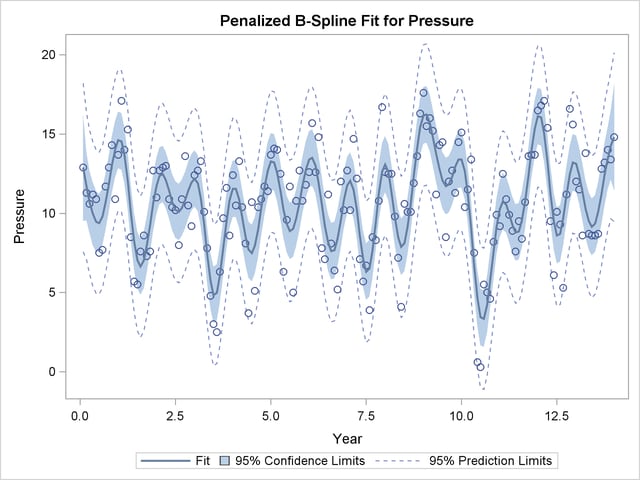
The results show a yearly cycle of pressure change. The procedure chose a smoothing parameter of 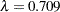. With data such as these, with many peaks and valleys, it might be useful to perform another analysis, this time asking for a smoother plot. The Schwarz Bayesian criterion (SBC) is sometimes a better choice than the default criterion when you want a smoother plot. The following PROC TRANSREG step requests a penalized B-spline analysis minimizing the SBC criterion:

proc transreg data=enso;
   model identity(pressure) = pbspline(year / sbc);
run;

The plot of SBC as a function of is shown in Output 91.3.2.

Output 91.3.2 Change in Atmospheric Pressure, SBC

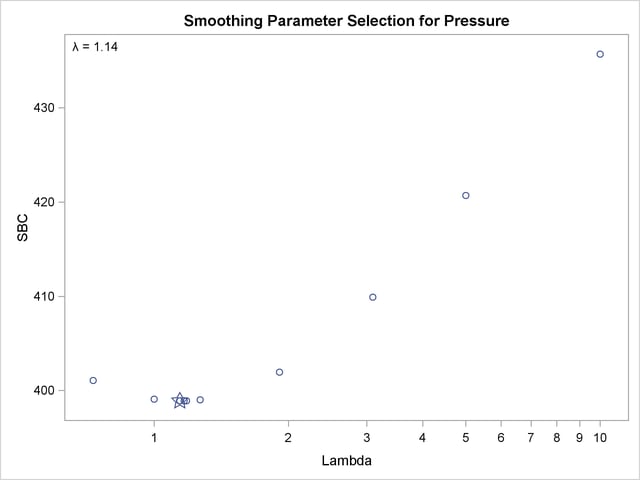
The fit plot (not shown) is essentially the same as the one shown in Output 91.3.1 due to the similar choice of smoothing parameters: 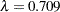versus 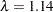. You can analyze these data again, this time forcing PROC TRANSREG to consider only larger smoothing parameters. The specification LAMBDA=2 10000 RANGE eliminates from consideration the two lambdas that you previously saw and considers only 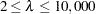. The following statements produce Output 91.3.3:

proc transreg data=enso;
   model identity(pressure) = pbspline(year / sbc lambda=2 10000 range);
run;

Output 91.3.3 Change in Atmospheric Pressure, SBC, Lambda > 1

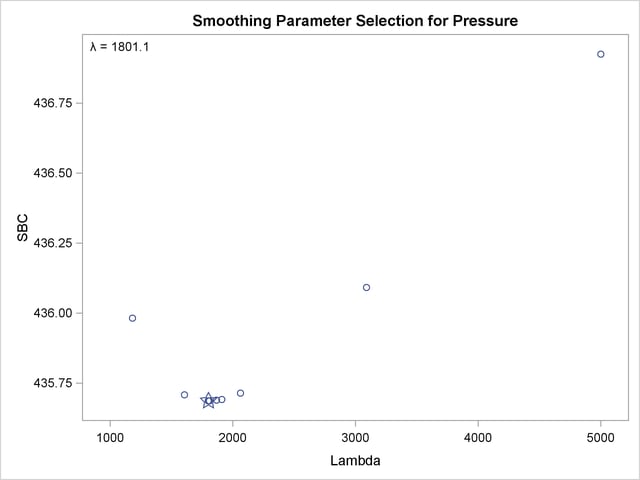
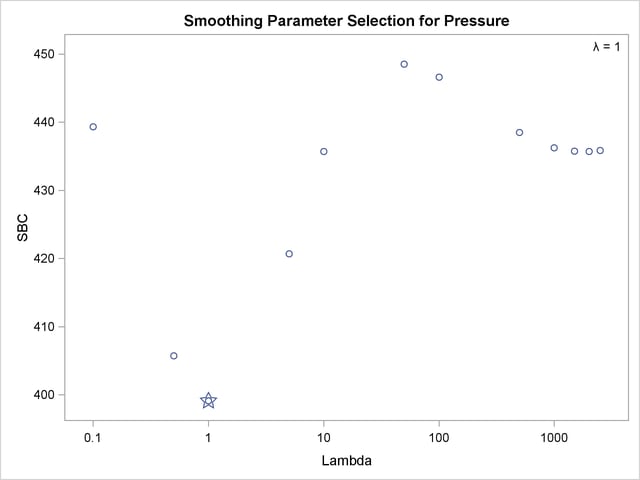
The results clearly show that there is a local minimum in the SBC() function at 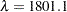. Using this lambda results in a much smoother regression function with a longer cycle than you saw previously. This second cycle can be identified as the periodic warming of the Pacific Ocean known as "El Niño." The SBC() function has at least two minima since there are at least two trends in the data. In the first analysis, PROC TRANSREG found what is probably the globally optimal solution, and in the second set of analyses, with a little nudging away from the global optimum, it found a very interesting locally optimal solution.

You can specify a list of lambdas to see SBC as a function of lambda over the range that includes both minima as follows:

proc transreg data=enso;
   model identity(pressure) = pbspline(year / sbc lambda=.1 .5 1 5
                                       10 50 100 500 to 2500 by 500);
run;

ods graphics off;

The plot of SBC as a function of is shown in Output 91.3.4.

Output 91.3.4 Change in Atmospheric Pressure, SBC, Over the Range of Both Minima