| The TRANSREG Procedure |
| Smoothing Splines |
You can use PROC TRANSREG to plot and output to a SAS data set the same smoothing spline function that the GPLOT procedure creates. You request a smoothing spline transformation by specifying SMOOTH in the MODEL statement. The smoothing parameter can be specified with either the SM= or the PARAMETER= o-option. The results are saved in the independent variable transformation (for example, Tx, when the independent variable is x) and the predicted values variable (for example, Py, when the dependent variable is y). The smooth regression function is displayed through PROC TRANSREG and ODS Graphics in Figure 91.41.
While you would normally display the results by using only PROC TRANSREG and ODS Graphics, you can also use PROC GPLOT to verify that the two procedures produce the same results. PROC GPLOT produces Figure 91.42. The PROC GPLOT plot request y * x = 1 displays the data as stars. The specification y * x = 2 with I=SM50 requests the smooth curve through the scatter plot. It is overlaid with Py * x = 3, which displays with large dots the smooth function created by PROC TRANSREG. The following statements produce Figure 91.41 and Figure 91.42:
title h=1.5 'Smoothing Splines';
ods graphics on;
data x;
do x = 1 to 100 by 2;
do rep = 1 to 3;
y = log(x) + sin(x / 10) + normal(7);
output;
end;
end;
run;
proc transreg;
model identity(y) = smooth(x / sm=50);
output p;
run;
proc gplot;
axis1 minor=none label=(angle=90 rotate=0);
axis2 minor=none;
symbol1 color=blue v=circle i=none; /* data */
symbol2 color=blue v=none i=sm50; /* gplot's smooth */
symbol3 color=red v=dot i=none; /* transreg's smooth */
plot y*x=1 y*x=2 py*x=3 / overlay haxis=axis2 vaxis=axis1 frame;
run; quit;
Note in Figure 91.42 that the smoothed values from PROC TRANSREG, shown by the large dots, exactly fall on the curve produced by PROC GPLOT.


You can plot multiple nonlinear functions, one for each of several groups as defined by the levels of a CLASS variable. When you cross a SMOOTH variable with a CLASS variable, specify ZERO=NONE with the CLASS expansion. The following statements create artificial data and produce Figure 91.43:
title2 'Two Groups';
data x;
do x = 1 to 100;
Group = 1;
do rep = 1 to 3;
y = log(x) + sin(x / 10) + normal(7);
output;
end;
group = 2;
do rep = 1 to 3;
y = -log(x) + cos(x / 10) + normal(7);
output;
end;
end;
run;
proc transreg ss2 data=x;
model identity(y) = class(group / zero=none) *
smooth(x / sm=50);
output p;
run;
ods graphics off;
The ANOVA table in Figure 91.43 shows the overall model fit. The degrees of freedom are based on the trace of the transformation hat matrix, and are typically not integers. The "Smooth Transformation" table reports the degrees of freedom for each term, which includes an intercept for each group; the regression coefficients, which are always 1 with smoothing splines; the 0 to 100 smoothing parameter (like the one PROC GPLOT uses); the actual computed smoothing parameter; and the name and label for each term.
| Smoothing Splines |
| Two Groups |
| Class Level Information | ||
|---|---|---|
| Class | Levels | Values |
| Group | 2 | 1 2 |

The SMOOTH transformation is valid only with independent variables. Typically, it is used only, as in the two preceding examples, in models with a single dependent variable, a single independent variable, and optionally, a single classification variable that is crossed with the independent variable. The various standardization options such as TSTANDARD=, CENTER, Z, and REFLECT are by default not permitted when the SMOOTH transformation is part of the model.
The SMOOTH transformation can also be used in other ways, but only when you specify the NSR a-option. The requirement that you specify the NSR a-option is new with this release. (See the section Smoothing Splines Changes and Enhancements.) When you specify the NSR a-option, and there are multiple independent variables designated as SMOOTH, PROC TRANSREG tries to smooth the 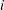 th independent variable by using the
th independent variable by using the 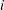 th dependent variable as a target. When there are more independent variables than dependent variables, the last dependent variable is reused as often as is necessary. For example, consider the following statements:
th dependent variable as a target. When there are more independent variables than dependent variables, the last dependent variable is reused as often as is necessary. For example, consider the following statements:
proc transreg nsr; model identity(y1-y3) = smooth(x1-x5); run;
Smoothing is based on the pairs (y1, x1), (y2, x2), (y3, x3), (y3, x4), and (y3, x5).
The SMOOTH transformation is a noniterative transformation. The smoothing of each variable occurs before the iterations begin. In contrast, SSPLINE provides an iterative smoothing spline transformation. It does not generally minimize squared error; hence, divergence is possible with SSPLINE.
Copyright © SAS Institute, Inc. All Rights Reserved.