PROC TPSPLINE: Large Data Set Application :: SAS/STAT(R) 9.22 User's Guide

The TPSPLINE Procedure

Example 90.4 Large Data Set Application

This example illustrates how you can use the D= option to decrease the computation time needed by the TPSPLINE procedure. Although the D= option can be helpful in decreasing computation time for large data sets, it might produce unexpected results when used with small data sets.

The following statements generate the data set large:

data large;
   do x=-5 to 5 by 0.02;
      y=5*sin(3*x)+1*rannor(57391);
      output;
   end;
run;

The data set large contains 501 observations with one independent variable x and one dependent variable y. The following statements invoke PROC TPSPLINE to produce a thin-plate smoothing spline estimate and the associated 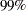$\text{[math]}$ confidence interval. The output statistics are saved in the data set fit1.

proc tpspline data=large;
   model y  =(x) /lognlambda=(-5 to -1 by 0.2) alpha=0.01;
   output out=fit1 pred lclm uclm;
run;

The results from this MODEL statement are displayed in Output 90.4.1.

Output 90.4.1 Output from PROC TPSPLINE without the D= Option

Raw Data

The TPSPLINE Procedure

Dependent Variable: y

Summary of Input Data Set
Number of Non-Missing Observations	501
Number of Missing Observations	0
Unique Smoothing Design Points	501

Summary of Final Model
Number of Regression Variables	0
Number of Smoothing Variables	1
Order of Derivative in the Penalty	2
Dimension of Polynomial Space	2

GCV Function
log10(n*Lambda)	GCV
-5.000000	1.258653
-4.800000	1.228743
-4.600000	1.205835
-4.400000	1.188371
-4.200000	1.174644
-4.000000	1.163102
-3.800000	1.152627
-3.600000	1.142590
-3.400000	1.132700
-3.200000	1.122789
-3.000000	1.112755
-2.800000	1.102642
-2.600000	1.092769
-2.400000	1.083779
-2.200000	1.076636
-2.000000	1.072763	*
-1.800000	1.074636
-1.600000	1.087152
-1.400000	1.120339
-1.200000	1.194023
-1.000000	1.344213

Note: * indicates minimum GCV value.

Summary Statistics of Final Estimation
log10(n*Lambda)	-1.9483
Smoothing Penalty	9953.7066
Residual SS	475.0984
Tr(I-A)	471.0861
Model DF	29.9139
Standard Deviation	1.0042
GCV	1.0726

The following statements specify an identical model, but with the additional specification of the D= option. The estimates are obtained by treating nearby points as replicates.

proc tpspline data=large;
   model y  =(x) /lognlambda=(-5 to -1 by 0.2) d=0.05 alpha=0.01;
   output out=fit2 pred lclm uclm;
run;

The output is displayed in Output 90.4.2.

Output 90.4.2 Output from PROC TPSPLINE with the D= Option

Raw Data

The TPSPLINE Procedure

Dependent Variable: y

Summary of Input Data Set
Number of Non-Missing Observations	501
Number of Missing Observations	0
Unique Smoothing Design Points	251

Summary of Final Model
Number of Regression Variables	0
Number of Smoothing Variables	1
Order of Derivative in the Penalty	2
Dimension of Polynomial Space	2

GCV Function
log10(n*Lambda)	GCV
-5.000000	1.306536
-4.800000	1.261692
-4.600000	1.226881
-4.400000	1.200060
-4.200000	1.179284
-4.000000	1.162776
-3.800000	1.149072
-3.600000	1.137120
-3.400000	1.126220
-3.200000	1.115884
-3.000000	1.105766
-2.800000	1.095730
-2.600000	1.085972
-2.400000	1.077066
-2.200000	1.069954
-2.000000	1.066076	*
-1.800000	1.067929
-1.600000	1.080419
-1.400000	1.113564
-1.200000	1.187172
-1.000000	1.337252

Note: * indicates minimum GCV value.

Summary Statistics of Final Estimation
log10(n*Lambda)	-1.9477
Smoothing Penalty	9943.5618
Residual SS	472.1424
Tr(I-A)	471.0901
Model DF	29.9099
Standard Deviation	1.0011
GCV	1.0659

The difference between the two estimates is minimal. However, the CPU time for the second MODEL statement is only about $\text{[math]}$ of the CPU time used in the first model fit.

The following statements produce a plot for comparison of the two estimates:

data fit2;
   set fit2;
   P1_y     = P_y;
   LCLM1_y  = LCLM_y;
   UCLM1_y  = UCLM_y;
   drop P_y LCLM_y UCLM_y;
 
proc sort data=fit1;
   by x y;
proc sort data=fit2;
   by x y;
 
data comp;
   merge fit1 fit2;
      by x y;
   label p1_y   ="Yhat1" p_y="Yhat0"
         lclm_y ="Lower CL"
         uclm_y ="Upper CL";
 
ods graphics on;
proc sgplot data=comp;
   title "Comparison of Two Estimates";
   title2 "with and without the D= Option";
 
   yaxis label="Predicted y Values";
   xaxis label="x";
 
   band x=x lower=lclm_y upper=uclm_y /name="range"
                      legendlabel="99% CI of Predicted y without D=";
   series x=x y=P_y/ name="P_y" legendlabel="Predicted y without D="
                      lineattrs=graphfit(thickness=1px pattern=shortdash);
   series x=x y=P1_y/ name="P1_y" legendlabel="Predicted y with D="
                      lineattrs=graphfit(thickness=1px color=red);
   discretelegend "range" "P_y" "P1_y";
run;
ods graphics off;

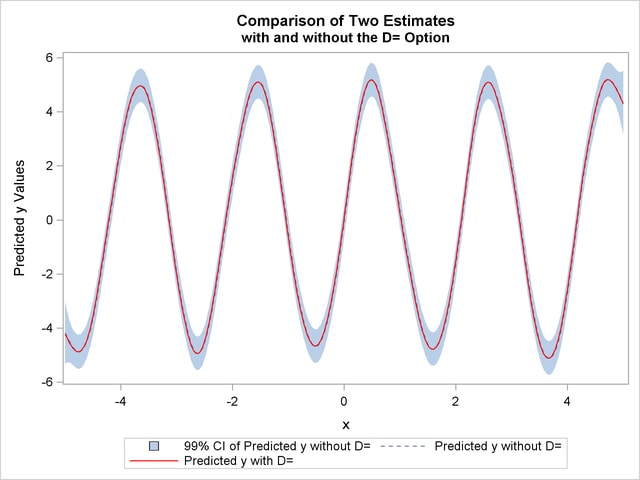
The estimates from fit1 and fit2 are displayed in Output 90.4.3 with the 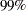$\text{[math]}$ confidence interval from the fit1 output data set.

Output 90.4.3 Comparison of Two PROC TPSPLINE Fits with and without the D= Option

Top of Page