| The SURVEYLOGISTIC Procedure |
Getting Started: SURVEYLOGISTIC Procedure
The SURVEYLOGISTIC procedure is similar to the LOGISTIC procedure and other regression procedures in the SAS System. See Chapter 51, The LOGISTIC Procedure, for general information about how to perform logistic regression by using SAS. PROC SURVEYLOGISTIC is designed to handle sample survey data, and thus it incorporates the sample design information into the analysis.
The following example illustrates how to use PROC SURVEYLOGISTIC to perform logistic regression for sample survey data.
In the customer satisfaction survey example in the section Getting Started: SURVEYSELECT Procedure of Chapter 89, The SURVEYSELECT Procedure, an Internet service provider conducts a customer satisfaction survey. The survey population consists of the company’s current subscribers from four states: Alabama (AL), Florida (FL), Georgia (GA), and South Carolina (SC). The company plans to select a sample of customers from this population, interview the selected customers and ask their opinions on customer service, and then make inferences about the entire population of subscribers from the sample data. A stratified sample is selected by using the probability proportional to size (PPS) method. The sample design divides the customers into strata depending on their types ('Old' or 'New') and their states (AL, FL, GA, SC). There are eight strata in all. Within each stratum, customers are selected and interviewed by using the PPS with replacement method, where the size variable is Usage. The stratified PPS sample contains 192 customers. The data are stored in the SAS data set SampleStrata. Figure 85.1 displays the first 10 observations of this data set.
| Customer Satisfaction Survey |
| Stratified PPS Sampling |
| (First 10 Observations) |
| Obs | State | Type | CustomerID | Rating | Usage | SamplingWeight |
|---|---|---|---|---|---|---|
| 1 | AL | New | 2178037 | Unsatisfied | 23.53 | 14.7473 |
| 2 | AL | New | 75375074 | Unsatisfied | 99.11 | 3.5012 |
| 3 | AL | New | 116722913 | Satisfied | 31.11 | 11.1546 |
| 4 | AL | New | 133059995 | Neutral | 52.70 | 19.7542 |
| 5 | AL | New | 216784622 | Satisfied | 8.86 | 39.1613 |
| 6 | AL | New | 225046040 | Neutral | 8.32 | 41.6960 |
| 7 | AL | New | 238463776 | Satisfied | 4.63 | 74.9483 |
| 8 | AL | New | 255918199 | Unsatisfied | 10.05 | 34.5405 |
| 9 | AL | New | 395767821 | Extremely Unsatisfied | 33.14 | 10.4719 |
| 10 | AL | New | 409095328 | Satisfied | 10.67 | 32.5295 |
In the SAS data set SampleStrata, the variable CustomerID uniquely identifies each customer. The variable State contains the state of the customer’s address. The variable Type equals 'Old' if the customer has subscribed to the service for more than one year; otherwise, the variable Type equals 'New'. The variable Usage contains the customer’s average monthly service usage, in hours. The variable Rating contains the customer’s responses to the survey. The sample design uses an unequal probability sampling method, with the sampling weights stored in the variable SamplingWeight.
The following SAS statements fit a cumulative logistic model between the satisfaction levels and the Internet usage by using the stratified PPS sample:
title 'Customer Satisfaction Survey'; proc surveylogistic data=SampleStrata; strata state type/list; model Rating (order=internal) = Usage; weight SamplingWeight; run;
The PROC SURVEYLOGISTIC statement invokes the SURVEYLOGISTIC procedure. The STRATA statement specifies the stratification variables State and Type that are used in the sample design. The LIST option requests a summary of the stratification. In the MODEL statement, Rating is the response variable and Usage is the explanatory variable. The ORDER=internal is used for the response variable Rating to ask the procedure to order the response levels by using the internal numerical value (1–5) instead of the formatted character value. The WEIGHT statement specifies the variable SamplingWeight that contains the sampling weights.
The results of this analysis are shown in the following figures.
| Customer Satisfaction Survey |
| Model Information | ||
|---|---|---|
| Data Set | WORK.SAMPLESTRATA | |
| Response Variable | Rating | |
| Number of Response Levels | 5 | |
| Stratum Variables | State | |
| Type | ||
| Number of Strata | 8 | |
| Weight Variable | SamplingWeight | Sampling Weight |
| Model | Cumulative Logit | |
| Optimization Technique | Fisher's Scoring | |
| Variance Adjustment | Degrees of Freedom (DF) | |
PROC SURVEYLOGISTIC first lists the following model fitting information and sample design information in Figure 85.2:
The link function is the logit of the cumulative of the lower response categories.
The Fisher scoring optimization technique is used to obtain the maximum likelihood estimates for the regression coefficients.
The response variable is Rating, which has five response levels.
The stratification variables are State and Type.
There are eight strata in the sample.
The weight variable is SamplingWeight.
The variance adjustment method used for the regression coefficients is the default degrees of freedom adjustment.
Figure 85.3 lists the number of observations in the data set and the number of observations used in the analysis. Since there is no missing value in this example, observations in the entire data set are used in the analysis. The sums of weights are also reported in this table.
The "Response Profile" table in Figure 85.4 lists the five response levels, their ordered values, and their total frequencies and total weights for each category. Due to the ORDER=INTERNAL option for the response variable Rating, the category "Extremely Unsatisfied" has the Ordered Value 1, the category "Unsatisfied" has the Ordered Value 2, and so on.
Figure 85.5 displays the output of the stratification summary. There are a total of eight strata, and each stratum is defined by the customer types within each state. The table also shows the number of customers within each stratum.
Figure 85.6 shows the chi-square test for testing the proportional odds assumption. The test is highly significant, which indicates that the cumulative logit model might not adequately fit the data.
Figure 85.7 shows the iteration algorithm converged to obtain the MLE for this example. The "Model Fit Statistics" table contains the Akaike information criterion (AIC), the Schwarz criterion (SC), and the negative of twice the log likelihood (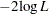 ) for the intercept-only model and the fitted model. AIC and SC can be used to compare different models, and the ones with smaller values are preferred.
) for the intercept-only model and the fitted model. AIC and SC can be used to compare different models, and the ones with smaller values are preferred.
The table "Testing Global Null Hypothesis: BETA=0" in Figure 85.8 shows the likelihood ratio test, the efficient score test, and the Wald test for testing the significance of the explanatory variable (Usage). All tests are significant.
Figure 85.9 shows the parameter estimates of the logistic regression and their standard errors.
| Analysis of Maximum Likelihood Estimates | ||||||
|---|---|---|---|---|---|---|
| Parameter | DF | Estimate | Standard Error |
Wald Chi-Square |
Pr > ChiSq | |
| Intercept | Extremely Unsatisfied | 1 | -2.0168 | 0.3988 | 25.5769 | <.0001 |
| Intercept | Unsatisfied | 1 | -1.0527 | 0.3543 | 8.8292 | 0.0030 |
| Intercept | Neutral | 1 | 0.1334 | 0.4189 | 0.1015 | 0.7501 |
| Intercept | Satisfied | 1 | 1.0751 | 0.5794 | 3.4432 | 0.0635 |
| Usage | 1 | 0.0377 | 0.0178 | 4.5212 | 0.0335 | |
Figure 85.10 displays the odds ratio estimate and its confidence limits.
Copyright © SAS Institute, Inc. All Rights Reserved.