| The SEQTEST Procedure |
Example 79.4 Testing a Binomial Proportion
This example tests a binomial proportion by using a four-stage group sequential design. Suppose a supermarket is developing a new store-brand coffee. From past studies, the positive response for the current store-brand coffee from customers is around 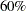 . The store is interested in whether the new brand has a better positive response than the current brand.
. The store is interested in whether the new brand has a better positive response than the current brand.
A power family method is used for the group sequential trial with the null hypothesis 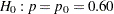 and a one-sided upper alternative with a power of
and a one-sided upper alternative with a power of 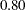 at
at 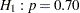 . To accommodate the zero null reference that is assumed in the SEQDESIGN procedure, an equivalent hypothesis
. To accommodate the zero null reference that is assumed in the SEQDESIGN procedure, an equivalent hypothesis 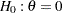 with
with  is used, where
is used, where 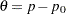 . The following statements request a power family method with early stopping to reject the null hypothesis:
. The following statements request a power family method with early stopping to reject the null hypothesis:
ods graphics on;
proc seqdesign altref=0.10
boundaryscale=mle
;
PowerFamily: design method=pow
nstages=4
alt=upper
beta=0.20
;
samplesize model=onesamplefreq( nullprop=0.6);
ods output Boundary=Bnd_Prop;
run;
ods graphics off;
The NULLPROP= option in the SAMPLESIZE statement specifies 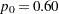 for the sample size computation. The ODS OUTPUT statement with the BOUNDARY=BND_PROP option creates an output data set named BND_PROP which contains the resulting boundary information for the subsequent sequential tests.
for the sample size computation. The ODS OUTPUT statement with the BOUNDARY=BND_PROP option creates an output data set named BND_PROP which contains the resulting boundary information for the subsequent sequential tests.
With the BOUNDARYSCALE=MLE option, the procedure displays the output boundaries in terms of the maximum likelihood estimates. The "Design Information" table in Output 79.4.1 displays design specifications and derived statistics. With the specified alternative reference 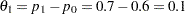 , the maximum information
, the maximum information 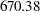 is also derived.
is also derived.
| Design Information | |
|---|---|
| Statistic Distribution | Normal |
| Boundary Scale | MLE |
| Alternative Hypothesis | Upper |
| Early Stop | Reject Null |
| Method | Power Family |
| Boundary Key | Both |
| Alternative Reference | 0.1 |
| Number of Stages | 4 |
| Alpha | 0.05 |
| Beta | 0.2 |
| Power | 0.8 |
| Max Information (Percent of Fixed Sample) | 108.4306 |
| Max Information | 670.3782 |
| Null Ref ASN (Percent of Fixed Sample) | 106.9276 |
| Alt Ref ASN (Percent of Fixed Sample) | 78.51072 |
The "Boundary Information" table in Output 79.4.2 displays the information level, alternative reference, and boundary values at each stage. With the STOP=REJECT option, only the rejection boundary values are displayed.
| Boundary Information (MLE Scale) Null Reference = 0 |
|||||
|---|---|---|---|---|---|
| _Stage_ | Alternative | Boundary Values | |||
| Information Level | Reference | Upper | |||
| Proportion | Actual | N | Upper | Alpha | |
| 1 | 0.2500 | 167.5945 | 35.19485 | 0.10000 | 0.20018 |
| 2 | 0.5000 | 335.1891 | 70.38971 | 0.10000 | 0.11903 |
| 3 | 0.7500 | 502.7836 | 105.5846 | 0.10000 | 0.08782 |
| 4 | 1.0000 | 670.3782 | 140.7794 | 0.10000 | 0.07077 |
With the specified ODS GRAPHICS ON statement, a detailed boundary plot with the rejection and acceptance regions is displayed, as shown in Output 79.4.3.
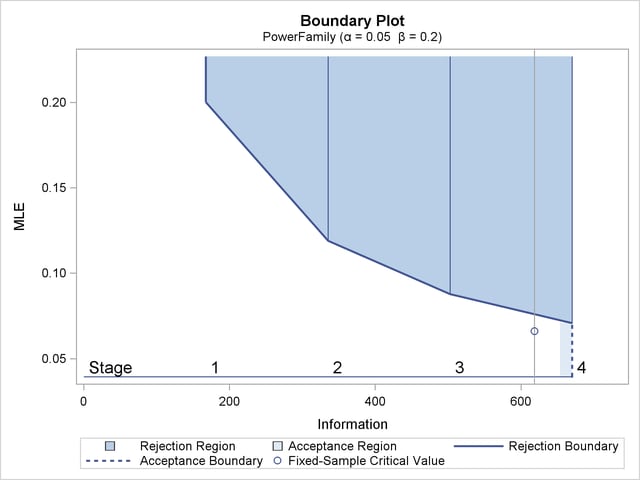
With the MODEL=ONESAMPLEFREQ option in the SAMPLESIZE statement, the "Sample Size Summary" table in Output 79.4.4 displays the parameters for the sample size computation.
The "Sample Sizes" table in Output 79.4.5 displays the required sample sizes for the group sequential clinical trial.
Thus,  customers are needed at stage
customers are needed at stage  , and
, and 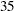 new customers are needed at each of the remaining stages. Suppose that
new customers are needed at each of the remaining stages. Suppose that  customers are available at stage
customers are available at stage  . Output 79.4.6 lists the 10 observations in the data set count_1.
. Output 79.4.6 lists the 10 observations in the data set count_1.
The Resp variable is an indicator variable with a value of  for a customer with a positive response and a value of
for a customer with a positive response and a value of 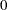 for a customer without a positive response.
for a customer without a positive response.
The following statements use the MEANS procedure to compute the mean response at stage  :
:
proc means data=Prop_1; var Resp; ods output Summary=Data_Prop1; run;
The following statements create and display (in Output 79.4.7) the data set for the centered mean positive response,  :
:
data Data_Prop1; set Data_Prop1; _Scale_='MLE'; _Stage_= 1; NObs= Resp_N; PDiff= Resp_Mean - 0.6; keep _Scale_ _Stage_ NObs PDiff; run; proc print data=Data_Prop1; title 'Statistics Computed at Stage 1'; run;
The following statements invoke the SEQTEST procedure to test for early stopping at stage  :
:
ods graphics on;
proc seqtest Boundary=Bnd_Prop
Data(Testvar=PDiff)=Data_Prop1
infoadj=prop
boundaryscale=mle
;
ods output Test=Test_Prop1;
run;
ods graphics off;
The BOUNDARY= option specifies the input data set that provides the boundary information for the trial at stage  , which was generated in the SEQDESIGN procedure. The DATA=DATA_PROP1 option specifies the input data set DATA_PROP1 that contains the test statistic and its associated sample size at stage
, which was generated in the SEQDESIGN procedure. The DATA=DATA_PROP1 option specifies the input data set DATA_PROP1 that contains the test statistic and its associated sample size at stage  , and the TESTVAR=PDIFF option identifies the test variable PDIFF in the data set.
, and the TESTVAR=PDIFF option identifies the test variable PDIFF in the data set.
If the computed information level for stage  is not the same as the value provided in the BOUNDARY= data set, the INFOADJ=PROP option (which is the default) proportionally adjusts the information levels at future interim stages from the levels provided in the BOUNDARY= data set. The BOUNDARYSCALE=MLE option displays the output boundaries in terms of the MLE scale.
is not the same as the value provided in the BOUNDARY= data set, the INFOADJ=PROP option (which is the default) proportionally adjusts the information levels at future interim stages from the levels provided in the BOUNDARY= data set. The BOUNDARYSCALE=MLE option displays the output boundaries in terms of the MLE scale.
The ODS OUTPUT statement with the TEST=TEST_PROP1 option creates an output data set named TEST_PROP1 which contains the updated boundary information for the test at stage  . The data set also provides the boundary information that is needed for the group sequential test at the next stage.
. The data set also provides the boundary information that is needed for the group sequential test at the next stage.
The "Design Information" table in Output 79.4.8 displays design specifications. By default (or equivalently if you specify BOUNDARYKEY=ALPHA), the boundary values are modified for the new information levels to maintain the Type I error probability  . The power has been modified for the new information levels.
. The power has been modified for the new information levels.
| Design Information | |
|---|---|
| BOUNDARY Data Set | WORK.BND_PROP |
| Data Set | WORK.DATA_PROP1 |
| Statistic Distribution | Normal |
| Boundary Scale | MLE |
| Alternative Hypothesis | Upper |
| Early Stop | Reject Null |
| Number of Stages | 4 |
| Alpha | 0.05 |
| Beta | 0.20015 |
| Power | 0.79985 |
| Max Information (Percent of Fixed Sample) | 108.4783 |
| Max Information | 670.378176 |
| Null Ref ASN (Percent of Fixed Sample) | 106.9684 |
| Alt Ref ASN (Percent of Fixed Sample) | 78.45899 |
The "Test Information" table in Output 79.4.9 displays the boundary values for the test statistic with the specified MLE scale.
| Test Information (MLE Scale) Null Reference = 0 |
|||||||
|---|---|---|---|---|---|---|---|
| _Stage_ | Alternative | Boundary Values | Test | ||||
| Information Level | Reference | Upper | PDiff | ||||
| Proportion | Actual | N | Upper | Alpha | Estimate | Action | |
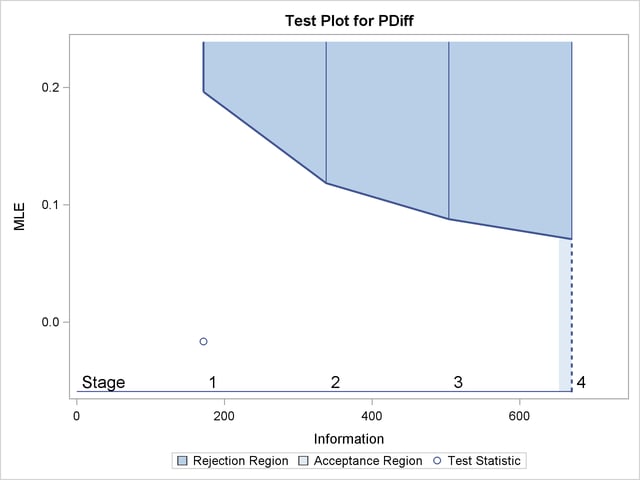
| 1 | 0.2557 | 171.4286 | 36 | 0.10000 | 0.19638 | -0.01667 | Continue |
| 2 | 0.5038 | 337.7451 | 70.92647 | 0.10000 | 0.11845 | . | |
| 3 | 0.7519 | 504.0616 | 105.8529 | 0.10000 | 0.08771 | . | |
| 4 | 1.0000 | 670.3782 | 140.7794 | 0.10000 | 0.07082 | . | |
The information level at stage  is computed as
is computed as 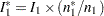 , where
, where  and
and  are the information level and sample size at stage
are the information level and sample size at stage  in the BOUNDARY= data set, and
in the BOUNDARY= data set, and 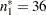 is the available sample size at stage
is the available sample size at stage  .
.
With the INFOADJ=PROP option (which is the default), the information levels at interim stages  and
and  are derived proportionally from the information levels in the BOUNDARY= data set. At stage
are derived proportionally from the information levels in the BOUNDARY= data set. At stage  , the statistic
, the statistic 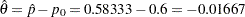 is less than the upper
is less than the upper  boundary value
boundary value  , so the trial continues to the next stage.
, so the trial continues to the next stage.
With the specified ODS GRAPHICS ON statement, a boundary plot with the rejection and acceptance regions is displayed, as shown in Output 79.4.10. As expected, the test statistic is in the continuation region.
The following statements use the MEANS procedure to compute the mean response at stage  :
:
proc means data=Prop_2; var Resp; ods output Summary=Data_Prop2; run;
The following statements create and display (in Output 79.4.11) the data set for the centered mean positive response ( ) at stage
) at stage  :
:
data Data_Prop2; set Data_Prop2; _Scale_='MLE'; _Stage_= 2; NObs= Resp_N; PDiff= Resp_Mean - 0.6; keep _Scale_ _Stage_ NObs PDiff; run; proc print data=Data_Prop2; title 'Statistics Computed at Stage 2'; run;
The following statements invoke the SEQTEST procedure to test for early stopping at stage  :
:
ods graphics on;
proc seqtest Boundary=Test_Prop1
Data(Testvar=PDiff)=Data_Prop2
infoadj=prop
boundaryscale=mle
condpower(cref=1)
predpower
plots=condpower
;
ods output test=Test_Prop2;
run;
ods graphics off;
The BOUNDARY= option specifies the input data set that provides the boundary information for the trial at stage  , which was generated by the SEQTEST procedure at the previous stage. The DATA= option specifies the input data set that contains the test statistic and its associated sample size at stage
, which was generated by the SEQTEST procedure at the previous stage. The DATA= option specifies the input data set that contains the test statistic and its associated sample size at stage  , and the TESTVAR= option identifies the test variable in the data set.
, and the TESTVAR= option identifies the test variable in the data set.
The ODS OUTPUT statement with the TEST=TEST_PROP2 option creates an output data set named TEST_PROP2 which contains the updated boundary information for the test at stage  . The data set also provides the boundary information that is needed for the group sequential test at the next stage.
. The data set also provides the boundary information that is needed for the group sequential test at the next stage.
The CONDPOWER(CREF=1) option requests the conditional power with the observed statistic under the alternative hypothesis, in addition to the conditional power under the hypothetical reference 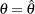 , the MLE estimate. The PREDPOWER option requests the noninformative predictive power with the observed statistic.
, the MLE estimate. The PREDPOWER option requests the noninformative predictive power with the observed statistic.
The "Test Information" table in Output 79.4.12 displays the boundary values for the test statistic with the specified MLE scale. The test statistic  is less than the corresponding upper
is less than the corresponding upper  boundary
boundary  , so the sequential test does not stop at stage
, so the sequential test does not stop at stage  to reject the null hypothesis.
to reject the null hypothesis.
| Test Information (MLE Scale) Null Reference = 0 |
|||||||
|---|---|---|---|---|---|---|---|
| _Stage_ | Alternative | Boundary Values | Test | ||||
| Information Level | Reference | Upper | PDiff | ||||
| Proportion | Actual | N | Upper | Alpha | Estimate | Action | |
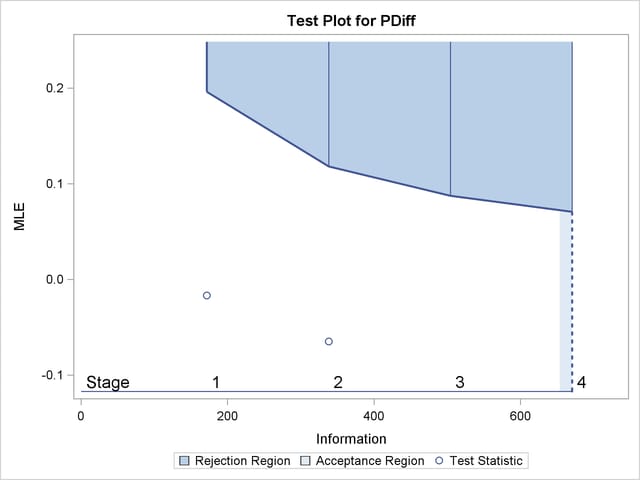
| 1 | 0.2557 | 171.4286 | 36 | 0.10000 | 0.19638 | -0.01667 | Continue |
| 2 | 0.5043 | 338.0952 | 71 | 0.10000 | 0.11834 | -0.06479 | Continue |
| 3 | 0.7522 | 504.2367 | 105.8897 | 0.10000 | 0.08769 | . | |
| 4 | 1.0000 | 670.3782 | 140.7794 | 0.10000 | 0.07082 | . | |
With the specified ODS GRAPHICS ON statement, the "Test Plot" displays boundary values of the design and the test statistic, as shown in Output 79.4.13. It also shows that the test statistic is in the "Continuation Region" below the upper  boundary value at stage
boundary value at stage  .
.
The predictive power is the probability to reject the null hypothesis under the posterior distribution with a noninformative prior given the observed statistic 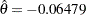 . The "Predictive Power Information" table in Output 79.4.14 indicates that the predictive power at
. The "Predictive Power Information" table in Output 79.4.14 indicates that the predictive power at 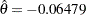 is
is 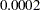 .
.
The "Conditional Power Information" table in Output 79.4.15 displays conditional powers given the observed statistic under hypothetical references 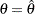 , the maximum likelihood estimate, and
, the maximum likelihood estimate, and 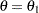 . The constant
. The constant  under CRef for the MLE is derived from
under CRef for the MLE is derived from 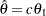 ; that is,
; that is,  .
.
The conditional power is the probability of rejecting the null hypothesis under these hypothetical references given the observed statistic 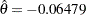 . The table in Output 79.4.15 shows a weak conditional power of
. The table in Output 79.4.15 shows a weak conditional power of  under the alternative hypothesis.
under the alternative hypothesis.
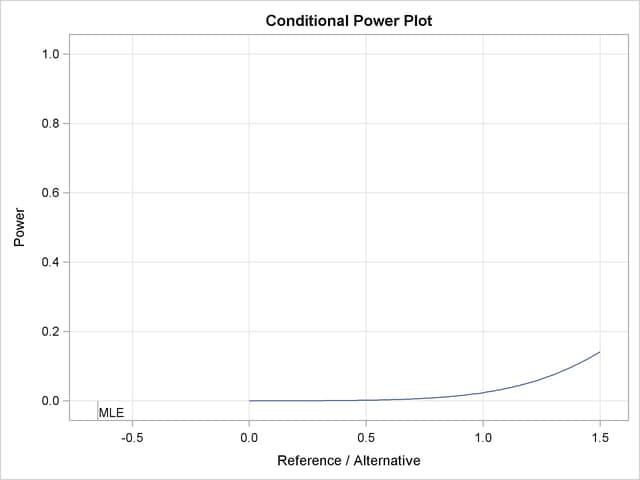
The "Conditional Power Plot" displays conditional powers given the observed statistic under various hypothetical references, as shown in Output 79.4.16. These references include 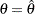 , the maximum likelihood estimate, and
, the maximum likelihood estimate, and 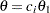 , where
, where  is the alternative reference and
is the alternative reference and  are constants that are specified in the CREF= option. Output 79.4.16 shows that the conditional power increases as
are constants that are specified in the CREF= option. Output 79.4.16 shows that the conditional power increases as  increases.
increases.
With a predictive power 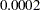 and a conditional power of
and a conditional power of  under
under  , the supermarket decides to stop the trial and accept the null hypothesis. That is, the positive response for the new store-brand coffee is not better than that for the current store-brand coffee.
, the supermarket decides to stop the trial and accept the null hypothesis. That is, the positive response for the new store-brand coffee is not better than that for the current store-brand coffee.
In the SEQTEST procedure, the conditional probability at an interim stage 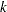 is the probability that the test statistic at the final stage (stage
is the probability that the test statistic at the final stage (stage 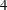 ) would exceed the rejection critical value. Since an interim stage exists between the current stage (stage
) would exceed the rejection critical value. Since an interim stage exists between the current stage (stage  ) and the final stage, the conditional power is not the conditional probability to reject the null hypothesis
) and the final stage, the conditional power is not the conditional probability to reject the null hypothesis  .
.
The following statements invoke the SEQTEST procedure to test for early stopping at stage  . The NSTAGES=3 option sets the next stage as the final stage (stage
. The NSTAGES=3 option sets the next stage as the final stage (stage 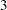 ). The CONDPOWER(CREF=1) option requests the conditional power with the observed statistic under the alternative hypothesis, in addition to the conditional power under the hypothetical reference
). The CONDPOWER(CREF=1) option requests the conditional power with the observed statistic under the alternative hypothesis, in addition to the conditional power under the hypothetical reference 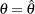 , the MLE estimate.
, the MLE estimate.
proc seqtest Boundary=Test_Prop1
Data(Testvar=PDiff)=Data_Prop2
nstages=3
boundaryscale=mle
condpower(cref=1)
;
run;
The "Test Information" table in Output 79.4.18 displays the boundary values for the test statistic with the specified MLE scale, assuming that the next stage is the final stage.
| Test Information (MLE Scale) Null Reference = 0 |
|||||||
|---|---|---|---|---|---|---|---|
| _Stage_ | Alternative | Boundary Values | Test | ||||
| Information Level | Reference | Upper | PDiff | ||||
| Proportion | Actual | N | Upper | Alpha | Estimate | Action | |
| 1 | 0.2557 | 171.4286 | 36 | 0.10000 | 0.19638 | -0.01667 | Continue |
| 2 | 0.5043 | 338.0952 | 71 | 0.10000 | 0.11834 | -0.06479 | Continue |
| 3 | 1.0000 | 670.3782 | 140.7794 | 0.10000 | 0.06730 | . | |
The "Conditional Power Information" table in Output 79.4.19 displays conditional powers given the observed statistic, assuming that the next stage is the final stage.
The conditional power is the probability of rejecting the null hypothesis under these hypothetical references given the observed statistic 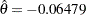 . The table in Output 79.4.19 also shows a weak conditional power of
. The table in Output 79.4.19 also shows a weak conditional power of 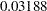 under the alternative hypothesis.
under the alternative hypothesis.
Copyright © SAS Institute, Inc. All Rights Reserved.