| The SEQTEST Procedure |
| Repeated Confidence Intervals |
In a group sequential test, repeated confidence intervals for a parameter  are defined as a sequence of intervals
are defined as a sequence of intervals 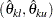 ,
, 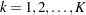 , for which a simultaneous coverage probability is maintained (Jennison and Turnbull 2000, p. 189). That is, a
, for which a simultaneous coverage probability is maintained (Jennison and Turnbull 2000, p. 189). That is, a 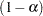 sequence of repeated confidence intervals has
sequence of repeated confidence intervals has
 |
These confidence limits 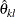 and
and 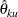 can be created from observed statistic and boundary values at each stage.
can be created from observed statistic and boundary values at each stage.
Two-Sided Repeated Confidence Intervals
Two sequences of repeated confidence intervals can be derived for a two-sided test. One is a 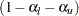 rejection repeated confidence intervals
rejection repeated confidence intervals  ,
, 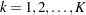 , and the other is a
, and the other is a 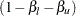 acceptance repeated confidence intervals
acceptance repeated confidence intervals 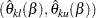 ,
, 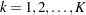 , where
, where  and
and 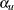 are the lower and upper Type I error probabilities for the test and
are the lower and upper Type I error probabilities for the test and 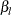 and
and 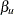 are the lower and upper Type II error probabilities for the test (Jennison and Turnbull 2000, p. 196).
are the lower and upper Type II error probabilities for the test (Jennison and Turnbull 2000, p. 196).
The rejection lower and upper repeated confidence limits at stage 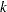 are
are
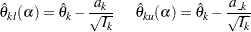 |
The hypothesis is rejected for upper alternative if the lower limit 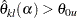 and is rejected for lower alternative if the upper limit
and is rejected for lower alternative if the upper limit 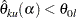 . That is, the hypothesis is rejected if both
. That is, the hypothesis is rejected if both 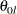 and
and 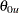 are not in a rejection repeated confidence interval
are not in a rejection repeated confidence interval  .
.
The acceptance lower and upper repeated confidence limits at stage 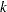 are
are
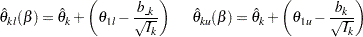 |
The hypothesis is accepted if the lower limit  and the upper limit
and the upper limit 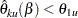 . That is, a repeated confidence interval is contained in the interval
. That is, a repeated confidence interval is contained in the interval 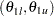 .
.
One-Sided Repeated Confidence Intervals
Like the two-sided repeated confidence intervals, two sequences of repeated confidence intervals can be derived for a one-sided test. Suppose the one-sided test has an upper alternative 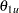 . Then one sequence of repeated confidence intervals is a
. Then one sequence of repeated confidence intervals is a  rejection repeated confidence intervals
rejection repeated confidence intervals  ,
, 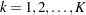 , and the other is a
, and the other is a  acceptance repeated confidence intervals
acceptance repeated confidence intervals 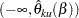 ,
, 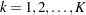 , where
, where 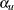 and
and 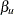 are the upper Type I and Type II error probabilities for the test. Thus, a sequence of repeated confidence intervals with confidence level greater than or equal to
are the upper Type I and Type II error probabilities for the test. Thus, a sequence of repeated confidence intervals with confidence level greater than or equal to 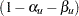 is given by
is given by 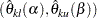 .
.
The rejection lower repeated confidence limit and the acceptance upper repeated confidence limit at stage 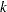 are
are
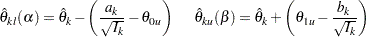 |
The hypothesis is rejected if the lower limit 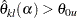 . and it is accepted if the upper limit
. and it is accepted if the upper limit 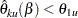 .
.
Copyright © SAS Institute, Inc. All Rights Reserved.