| The SEQTEST Procedure |
| Stochastic Curtailment |
Lan, Simon, and Halperin (1982) introduce stochastic curtailment to stop a trial if, given current data, it is likely to predict the outcome of the trial with high probability. That is, a trial can be stopped to reject the null hypothesis  if the conditional probability of rejecting
if the conditional probability of rejecting  under
under  , given current data in the analyses at the end of the trial, is greater than
, given current data in the analyses at the end of the trial, is greater than 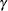 , where the constant
, where the constant 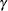 should be between
should be between  and
and  , and values of
, and values of  or
or 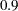 are recommended (Jennison and Turnbull 2000, p. 206). Similarly, a trial can be stopped to accept the null hypothesis
are recommended (Jennison and Turnbull 2000, p. 206). Similarly, a trial can be stopped to accept the null hypothesis  if the conditional probability of rejecting
if the conditional probability of rejecting  under the alternative hypothesis
under the alternative hypothesis 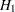 , given current data in the analyses at the end of the trial, is less than
, given current data in the analyses at the end of the trial, is less than 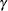 .
.
The following two approaches for stochastic curtailment are available in the SEQTEST procedures: conditional power approach and predictive power approach. For each approach, the derived group sequential test is used as the reference test for rejection.
Conditional Power Approach
In the SEQTEST procedure, the conditional power at an interim stage 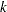 is the probability that the test statistic at the final stage (stage
is the probability that the test statistic at the final stage (stage 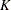 ) would exceed the rejection critical value (Cui, Hung, and Wang 1999, p. 854; Emerson, Kittelson, and Gillen 2005, p. 13). If there exist interim stages between the
) would exceed the rejection critical value (Cui, Hung, and Wang 1999, p. 854; Emerson, Kittelson, and Gillen 2005, p. 13). If there exist interim stages between the 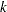 th stage and the final stage,
th stage and the final stage, 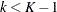 , the conditional power is not the conditional probability to reject the null hypothesis
, the conditional power is not the conditional probability to reject the null hypothesis  . In this case, you can set the next stage as the final stage, and the conditional power is the conditional probability to reject
. In this case, you can set the next stage as the final stage, and the conditional power is the conditional probability to reject  .
.
The conditional distribution of 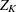 given the observed statistic
given the observed statistic  at the
at the 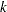 th stage and the hypothetical reference
th stage and the hypothetical reference  is
is
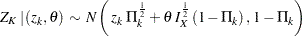 |
where 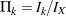 is the fraction of information at the
is the fraction of information at the 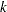 th stage.
th stage.
The power for the upper alternative, 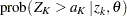 , is then given by
, is then given by
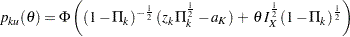 |
where  is the cumulative distribution function of the standardized
is the cumulative distribution function of the standardized 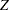 statistic and
statistic and 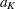 is the upper critical value at the final stage.
is the upper critical value at the final stage.
Similarly, the power for the lower alternative,  , is
, is
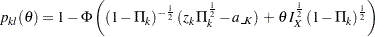 |
where 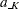 is the lower critical value at the final stage.
is the lower critical value at the final stage.
A special case of the conditional power is the futility index (Ware, Muller, and Braunwald, 1985). It is one minus the conditional power under 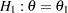 :
:
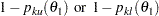 |
That is, it is the probability of accepting the null hypothesis under the alternative hypothesis given current data. A high futility index indicates a small probability of success (rejecting  ) given the current data.
) given the current data.
If 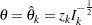 , the maximum likelihood estimate at stage
, the maximum likelihood estimate at stage 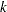 , the powers for the upper and lower alternatives can be simplified:
, the powers for the upper and lower alternatives can be simplified:
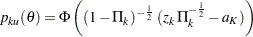 |
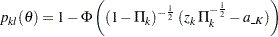 |
Predictive Power Approach
The conditional power depends on the specified reference  , which might be supported by the current data (Jennison and Turnbull 2000, p. 210). An alternative is to use the predictive power (Herson 1979), which is a weighted average of the conditional power over values of
, which might be supported by the current data (Jennison and Turnbull 2000, p. 210). An alternative is to use the predictive power (Herson 1979), which is a weighted average of the conditional power over values of  . Without prior knowledge about
. Without prior knowledge about  , then with
, then with 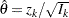 , the maximum likelihood estimate at stage
, the maximum likelihood estimate at stage 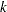 , the posterior distribution for
, the posterior distribution for  (Jennison and Turnbull 2000, p. 211) is
(Jennison and Turnbull 2000, p. 211) is
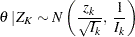 |
Thus, the predictive power at stage 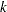 for the upper and lower alternatives can be derived as
for the upper and lower alternatives can be derived as
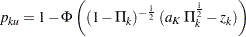 |
 |
where 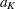 and
and 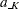 are the upper and lower critical values at the final stage.
are the upper and lower critical values at the final stage.
Copyright © SAS Institute, Inc. All Rights Reserved.