| The REG Procedure |
| Models of Less Than Full Rank |
If the model is not full rank, there are an infinite number of least squares solutions for the estimates. PROC REG chooses a nonzero solution for all variables that are linearly independent of previous variables and a zero solution for other variables. This solution corresponds to using a generalized inverse in the normal equations, and the expected values of the estimates are the Hermite normal form of  multiplied by the true parameters:
multiplied by the true parameters:
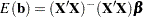 |
Degrees of freedom for the zeroed estimates are reported as zero. The hypotheses that are not testable have  tests reported as missing. The message that the model is not full rank includes a display of the relations that exist in the matrix.
tests reported as missing. The message that the model is not full rank includes a display of the relations that exist in the matrix.
The following statements use the fitness data from Example 74.2. The variable Dif=RunPulse RestPulse is created. When this variable is included in the model along with RunPulse and RestPulse, there is a linear dependency (or exact collinearity) between the independent variables. Figure 74.48 shows how this problem is diagnosed.
RestPulse is created. When this variable is included in the model along with RunPulse and RestPulse, there is a linear dependency (or exact collinearity) between the independent variables. Figure 74.48 shows how this problem is diagnosed.
data fit2; set fitness; Dif=RunPulse-RestPulse; proc reg data=fit2; model Oxygen=RunTime Age Weight RunPulse MaxPulse RestPulse Dif; run;
| Analysis of Variance | |||||
|---|---|---|---|---|---|
| Source | DF | Sum of Squares |
Mean Square |
F Value | Pr > F |
| Model | 6 | 722.54361 | 120.42393 | 22.43 | <.0001 |
| Error | 24 | 128.83794 | 5.36825 | ||
| Corrected Total | 30 | 851.38154 | |||
| Root MSE | 2.31695 | R-Square | 0.8487 |
|---|---|---|---|
| Dependent Mean | 47.37581 | Adj R-Sq | 0.8108 |
| Coeff Var | 4.89057 |
| Parameter Estimates | |||||
|---|---|---|---|---|---|
| Variable | DF | Parameter Estimate |
Standard Error |
t Value | Pr > |t| |
| Intercept | 1 | 102.93448 | 12.40326 | 8.30 | <.0001 |
| RunTime | 1 | -2.62865 | 0.38456 | -6.84 | <.0001 |
| Age | 1 | -0.22697 | 0.09984 | -2.27 | 0.0322 |
| Weight | 1 | -0.07418 | 0.05459 | -1.36 | 0.1869 |
| RunPulse | B | -0.36963 | 0.11985 | -3.08 | 0.0051 |
| MaxPulse | 1 | 0.30322 | 0.13650 | 2.22 | 0.0360 |
| RestPulse | B | -0.02153 | 0.06605 | -0.33 | 0.7473 |
| Dif | 0 | 0 | . | . | . |
PROC REG produces a message informing you that the model is less than full rank. Parameters with DF=0 are not estimated, and parameters with DF=B are biased. In addition, the form of the linear dependency among the regressors is displayed.
Copyright © SAS Institute, Inc. All Rights Reserved.