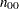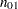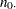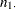Overview of Conditional McNemar tests

Notation:

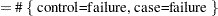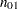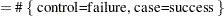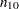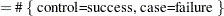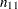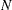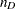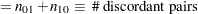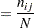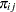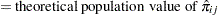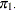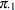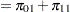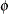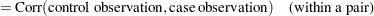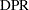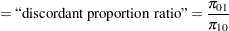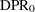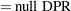Power formulas are given here in terms of the discordant proportions 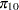and . If the input is specified in terms of 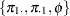, then it can be converted into values for 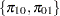as follows:

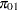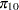All McNemar tests covered in PROC POWER are conditional, meaning that 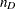is assumed fixed at its observed value.

For the usual 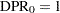, the hypotheses are

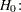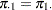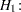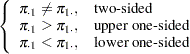The test statistic for both tests covered in PROC POWER (DIST=EXACT_COND and DIST=NORMAL) is the McNemar statistic 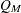, which has the following form when :

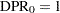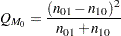For the conditional McNemar tests, this is equivalent to the square of the 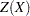statistic for the test of a single proportion (normal approximation to binomial), where the proportion is 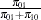, the null is 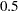, and "" is 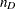(see, for example, Schork and Williams 1980):

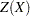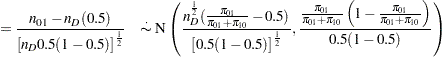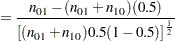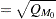This can be generalized to a custom null for 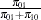, which is equivalent to specifying a custom null DPR:

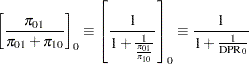So, a conditional McNemar test (asymptotic or exact) with a custom null is equivalent to the test of a single proportion 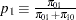with a null value 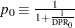, with a sample size of :

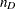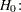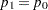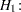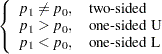which is equivalent to

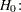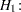The general form of the test statistic is thus

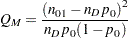The two most common conditional McNemar tests assume either the exact conditional distribution of 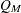(covered by the DIST=EXACT_COND analysis) or a standard normal distribution for 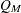(covered by the DIST=NORMAL analysis).

McNemar Exact Conditional Test (TEST=MCNEMAR DIST=EXACT_COND)

For DIST=EXACT_COND, the power is calculated assuming that the test is conducted by using the exact conditional distribution of 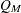(conditional on 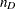). The power is calculated by first computing the conditional power for each possible 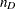. The unconditional power is computed as a weighted average over all possible outcomes of :

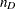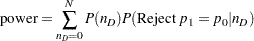where 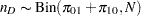, and 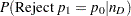is calculated by using the exact method in the section Exact Test of a Binomial Proportion (TEST=EXACT).

The achieved significance level, reported as "Actual Alpha" in the analysis, is computed in the same way except by using the actual alpha of the one-sample test in place of its power:

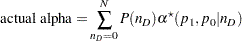where 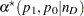is the actual alpha calculated by using the exact method in the section Exact Test of a Binomial Proportion (TEST=EXACT) with proportion , null , and sample size .

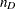McNemar Normal Approximation Test (TEST=MCNEMAR DIST=NORMAL)

For DIST=NORMAL, power is calculated assuming the test is conducted by using the normal-approximate distribution of 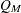(conditional on ).

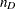For the METHOD=EXACT option, the power is calculated in the same way as described in the section McNemar Exact Conditional Test (TEST=MCNEMAR DIST=EXACT_COND), except that 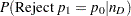is calculated by using the exact method in the section z Test for Binomial Proportion Using Null Variance (TEST=Z VAREST=NULL). The achieved significance level is calculated in the same way as described at the end of the section McNemar Exact Conditional Test (TEST=MCNEMAR DIST=EXACT_COND).

For the METHOD=MIETTINEN option, approximate sample size for the one-sided cases is computed according to equation (5.6) in Miettinen (1968):

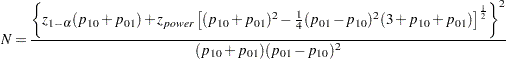Approximate power for the one-sided cases is computed by solving the sample size equation for power, and approximate power for the two-sided case follows easily by summing the one-sided powers each at :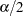

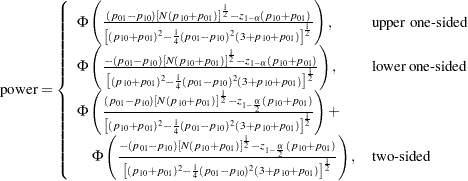The two-sided solution for is obtained by numerically inverting the power equation.

In general, compared to METHOD=CONNOR, the METHOD=MIETTINEN approximation tends to be slightly more accurate but can be slightly anticonservative in the sense of underestimating sample size and overestimating power (Lachin 1992, p. 1250).

For the METHOD=CONNOR option, approximate sample size for the one-sided cases is computed according to equation (3) in Connor (1987):

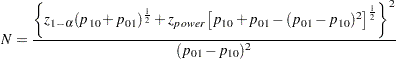Approximate power for the one-sided cases is computed by solving the sample size equation for power, and approximate power for the two-sided case follows easily by summing the one-sided powers each at :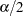

The two-sided solution for is obtained by numerically inverting the power equation.

In general, compared to METHOD=MIETTINEN, the METHOD=CONNOR approximation tends to be slightly less accurate but slightly conservative in the sense of overestimating sample size and underestimating power (Lachin 1992, p. 1250).