| The PHREG Procedure |
Example 64.11 Analysis of Clustered Data
When experimental units are naturally or artificially clustered, failure times of experimental units within a cluster are correlated. Lee, Wei, and Amato (1992) estimate the regression parameters in the Cox model by the maximum partial likelihood estimates under an independent working assumption and use a robust sandwich covariance matrix estimate to account for the intracluster dependence. A subset of data from the Diabetic Retinopathy Study (DRS) is used to illustrate the methodology as in Lin (1994).
The following DATA step creates the data set Blind that represents 197 diabetic patients who have a high risk of experiencing blindness in both eyes as defined by DRS criteria. One eye of each patient is treated with laser photocoagulation. The hypothesis of interest is whether the laser treatment delays the occurrence of blindness. Since juvenile and adult diabetes have very different courses, it is also desirable to examine how the age of onset of diabetes might affect the time of blindness. Since there are no biological differences between the left eye and the right eye, it is natural to assume a common baseline hazard function for the failure times of the left and right eyes.
Each patient is a cluster that contributes two observations to the input data set, one for each eye. The following variables are in the input data set Blind:
ID, patient’s identification
Time, failure time
Status, event indicator (0=censored and 1=uncensored)
Treatment, treatment received (1=laser photocoagulation and 0=otherwise)
DiabeticType, type of diabetes (0=juvenile onset with age of onset at 20 or under, and 1= adult onset with age of onset over 20)
data Blind; input ID Time Status DiabeticType Treatment @@; datalines; 5 46.23 0 1 1 5 46.23 0 1 0 14 42.50 0 0 1 14 31.30 1 0 0 16 42.27 0 0 1 16 42.27 0 0 0 25 20.60 0 0 1 25 20.60 0 0 0 29 38.77 0 0 1 29 0.30 1 0 0 46 65.23 0 0 1 46 54.27 1 0 0 49 63.50 0 0 1 49 10.80 1 0 0 56 23.17 0 0 1 56 23.17 0 0 0 61 1.47 0 0 1 61 1.47 0 0 0 71 58.07 0 1 1 71 13.83 1 1 0 100 46.43 1 1 1 100 48.53 0 1 0 112 44.40 0 1 1 112 7.90 1 1 0 120 39.57 0 1 1 120 39.57 0 1 0 127 30.83 1 1 1 127 38.57 1 1 0 133 66.27 0 1 1 133 14.10 1 1 0 150 20.17 1 0 1 150 6.90 1 0 0 167 58.43 0 1 1 167 41.40 1 1 0 176 58.20 0 0 1 176 58.20 0 0 0 ... more lines ... 1727 49.97 0 1 1 1727 2.90 1 1 0 1746 45.90 0 0 1 1746 1.43 1 0 0 1749 41.93 0 1 1 1749 41.93 0 1 0 ; run;
As a preliminary analysis, PROC FREQ is used to break down the numbers of blindness in the control and treated eyes:
proc freq data=Blind; table Treatment*Status; run;
By the end of the study, 54 treated eyes and 101 untreated eyes have developed blindness (Output 64.11.1).
The analysis of Lee, Wei, and Amato (1992) can be carried out by the following PROC PHREG specification. The explanatory variables in this Cox model are Treatment, DiabeticType, and the Treatment  DiabeticType interaction. The COVS(AGGREGATE) is specified to compute the robust sandwich covariance matrix estimate.
DiabeticType interaction. The COVS(AGGREGATE) is specified to compute the robust sandwich covariance matrix estimate.
proc phreg data=Blind covs(aggregate) namelen=22; model Time*Status(0)=Treatment DiabeticType Treatment*DiabeticType; id ID; run;
The robust standard error estimates are smaller than the model-based counterparts (Output 64.11.2), since the ratio of the robust standard error estimate relative to the model-based estimate is less than 1 for each variable. Laser photocoagulation appears to be effective (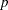 =0.0217) in delaying the occurrence of blindness. The effect is much more prominent for adult-onset diabetes than for juvenile-onset diabetes.
=0.0217) in delaying the occurrence of blindness. The effect is much more prominent for adult-onset diabetes than for juvenile-onset diabetes.
| Wei-Lin-Weissfeld Model |
| Analysis of Maximum Likelihood Estimates | ||||||||
|---|---|---|---|---|---|---|---|---|
| Parameter | DF | Parameter Estimate |
Standard Error |
StdErr Ratio |
Chi-Square | Pr > ChiSq | Hazard Ratio |
Label |
| Treatment | 1 | -0.42467 | 0.18497 | 0.850 | 5.2713 | 0.0217 | . | |
| DiabeticType | 1 | 0.34084 | 0.19558 | 0.982 | 3.0371 | 0.0814 | . | |
| Treatment*DiabeticType | 1 | -0.84566 | 0.30353 | 0.865 | 7.7622 | 0.0053 | . | Treatment * DiabeticType |
Copyright © SAS Institute, Inc. All Rights Reserved.