| The PHREG Procedure |
Example 64.1 Stepwise Regression
Krall, Uthoff, and Harley (1975) analyzed data from a study on multiple myeloma in which researchers treated 65 patients with alkylating agents. Of those patients, 48 died during the study and 17 survived. The following DATA step creates the data set Myeloma. The variable Time represents the survival time in months from diagnosis. The variable VStatus consists of two values, 0 and 1, indicating whether the patient was alive or dead, respectively, at the end of the study. If the value of VStatus is 0, the corresponding value of Time is censored. The variables thought to be related to survival are LogBUN (log(BUN) at diagnosis), HGB (hemoglobin at diagnosis), Platelet (platelets at diagnosis: 0=abnormal, 1=normal), Age (age at diagnosis, in years), LogWBC (log(WBC) at diagnosis), Frac (fractures at diagnosis: 0=none, 1=present), LogPBM (log percentage of plasma cells in bone marrow), Protein (proteinuria at diagnosis), and SCalc (serum calcium at diagnosis). Interest lies in identifying important prognostic factors from these nine explanatory variables.
data Myeloma;
input Time VStatus LogBUN HGB Platelet Age LogWBC Frac
LogPBM Protein SCalc;
label Time='Survival Time'
VStatus='0=Alive 1=Dead';
datalines;
1.25 1 2.2175 9.4 1 67 3.6628 1 1.9542 12 10
1.25 1 1.9395 12.0 1 38 3.9868 1 1.9542 20 18
2.00 1 1.5185 9.8 1 81 3.8751 1 2.0000 2 15
2.00 1 1.7482 11.3 0 75 3.8062 1 1.2553 0 12
2.00 1 1.3010 5.1 0 57 3.7243 1 2.0000 3 9
3.00 1 1.5441 6.7 1 46 4.4757 0 1.9345 12 10
5.00 1 2.2355 10.1 1 50 4.9542 1 1.6628 4 9
5.00 1 1.6812 6.5 1 74 3.7324 0 1.7324 5 9
6.00 1 1.3617 9.0 1 77 3.5441 0 1.4624 1 8
6.00 1 2.1139 10.2 0 70 3.5441 1 1.3617 1 8
6.00 1 1.1139 9.7 1 60 3.5185 1 1.3979 0 10
6.00 1 1.4150 10.4 1 67 3.9294 1 1.6902 0 8
7.00 1 1.9777 9.5 1 48 3.3617 1 1.5682 5 10
7.00 1 1.0414 5.1 0 61 3.7324 1 2.0000 1 10
7.00 1 1.1761 11.4 1 53 3.7243 1 1.5185 1 13
9.00 1 1.7243 8.2 1 55 3.7993 1 1.7404 0 12
11.00 1 1.1139 14.0 1 61 3.8808 1 1.2788 0 10
11.00 1 1.2304 12.0 1 43 3.7709 1 1.1761 1 9
11.00 1 1.3010 13.2 1 65 3.7993 1 1.8195 1 10
11.00 1 1.5682 7.5 1 70 3.8865 0 1.6721 0 12
11.00 1 1.0792 9.6 1 51 3.5051 1 1.9031 0 9
13.00 1 0.7782 5.5 0 60 3.5798 1 1.3979 2 10
14.00 1 1.3979 14.6 1 66 3.7243 1 1.2553 2 10
15.00 1 1.6021 10.6 1 70 3.6902 1 1.4314 0 11
16.00 1 1.3424 9.0 1 48 3.9345 1 2.0000 0 10
16.00 1 1.3222 8.8 1 62 3.6990 1 0.6990 17 10
17.00 1 1.2304 10.0 1 53 3.8808 1 1.4472 4 9
17.00 1 1.5911 11.2 1 68 3.4314 0 1.6128 1 10
18.00 1 1.4472 7.5 1 65 3.5682 0 0.9031 7 8
19.00 1 1.0792 14.4 1 51 3.9191 1 2.0000 6 15
19.00 1 1.2553 7.5 0 60 3.7924 1 1.9294 5 9
24.00 1 1.3010 14.6 1 56 4.0899 1 0.4771 0 9
25.00 1 1.0000 12.4 1 67 3.8195 1 1.6435 0 10
26.00 1 1.2304 11.2 1 49 3.6021 1 2.0000 27 11
32.00 1 1.3222 10.6 1 46 3.6990 1 1.6335 1 9
35.00 1 1.1139 7.0 0 48 3.6532 1 1.1761 4 10
37.00 1 1.6021 11.0 1 63 3.9542 0 1.2041 7 9
41.00 1 1.0000 10.2 1 69 3.4771 1 1.4771 6 10
41.00 1 1.1461 5.0 1 70 3.5185 1 1.3424 0 9
51.00 1 1.5682 7.7 0 74 3.4150 1 1.0414 4 13
52.00 1 1.0000 10.1 1 60 3.8573 1 1.6532 4 10
54.00 1 1.2553 9.0 1 49 3.7243 1 1.6990 2 10
58.00 1 1.2041 12.1 1 42 3.6990 1 1.5798 22 10
66.00 1 1.4472 6.6 1 59 3.7853 1 1.8195 0 9
67.00 1 1.3222 12.8 1 52 3.6435 1 1.0414 1 10
88.00 1 1.1761 10.6 1 47 3.5563 0 1.7559 21 9
89.00 1 1.3222 14.0 1 63 3.6532 1 1.6232 1 9
92.00 1 1.4314 11.0 1 58 4.0755 1 1.4150 4 11
4.00 0 1.9542 10.2 1 59 4.0453 0 0.7782 12 10
4.00 0 1.9243 10.0 1 49 3.9590 0 1.6232 0 13
7.00 0 1.1139 12.4 1 48 3.7993 1 1.8573 0 10
7.00 0 1.5315 10.2 1 81 3.5911 0 1.8808 0 11
8.00 0 1.0792 9.9 1 57 3.8325 1 1.6532 0 8
12.00 0 1.1461 11.6 1 46 3.6435 0 1.1461 0 7
11.00 0 1.6128 14.0 1 60 3.7324 1 1.8451 3 9
12.00 0 1.3979 8.8 1 66 3.8388 1 1.3617 0 9
13.00 0 1.6628 4.9 0 71 3.6435 0 1.7924 0 9
16.00 0 1.1461 13.0 1 55 3.8573 0 0.9031 0 9
19.00 0 1.3222 13.0 1 59 3.7709 1 2.0000 1 10
19.00 0 1.3222 10.8 1 69 3.8808 1 1.5185 0 10
28.00 0 1.2304 7.3 1 82 3.7482 1 1.6721 0 9
41.00 0 1.7559 12.8 1 72 3.7243 1 1.4472 1 9
53.00 0 1.1139 12.0 1 66 3.6128 1 2.0000 1 11
57.00 0 1.2553 12.5 1 66 3.9685 0 1.9542 0 11
77.00 0 1.0792 14.0 1 60 3.6812 0 0.9542 0 12
;
The stepwise selection process consists of a series of alternating forward selection and backward elimination steps. The former adds variables to the model, while the latter removes variables from the model.
The following statements use PROC PHREG to produce a stepwise regression analyis. Stepwise selection is requested by specifying the SELECTION=STEPWISE option in the MODEL statement. The option SLENTRY=0.25 specifies that a variable has to be significant at the 0.25 level before it can be entered into the model, while the option SLSTAY=0.15 specifies that a variable in the model has to be significant at the 0.15 level for it to remain in the model. The DETAILS option requests detailed results for the variable selection process.
proc phreg data=Myeloma;
model Time*VStatus(0)=LogBUN HGB Platelet Age LogWBC
Frac LogPBM Protein SCalc
/ selection=stepwise slentry=0.25
slstay=0.15 details;
run;
Results of the stepwise regression analysis are displayed in Output 64.1.1 through Output 64.1.7.
Individual score tests are used to determine which of the nine explanatory variables is first selected into the model. In this case, the score test for each variable is the global score test for the model containing that variable as the only explanatory variable. Output 64.1.1 displays the chi-square statistics and the corresponding p-values. The variable LogBUN has the largest chi-square value (8.5164), and it is significant (p=0.0035) at the SLENTRY=0.25 level. The variable LogBUN is thus entered into the model.
| Model Information | ||
|---|---|---|
| Data Set | WORK.MYELOMA | |
| Dependent Variable | Time | Survival Time |
| Censoring Variable | VStatus | 0=Alive 1=Dead |
| Censoring Value(s) | 0 | |
| Ties Handling | BRESLOW | |
| Summary of the Number of Event and Censored Values |
|||
|---|---|---|---|
| Total | Event | Censored | Percent Censored |
| 65 | 48 | 17 | 26.15 |
Output 64.1.2 displays the results of the first model. Since the Wald chi-square statistic is significant (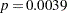 ) at the SLSTAY=0.15 level, LogBUN stays in the model.
) at the SLSTAY=0.15 level, LogBUN stays in the model.
| Convergence Status |
|---|
| Convergence criterion (GCONV=1E-8) satisfied. |
| Model Fit Statistics | ||
|---|---|---|
| Criterion | Without Covariates |
With Covariates |
| -2 LOG L | 309.716 | 301.959 |
| AIC | 309.716 | 303.959 |
| SBC | 309.716 | 305.830 |
The next step consists of selecting another variable to add to the model. Output 64.1.3 displays the chi-square statistics and p-values of individual score tests (adjusted for LogBUN) for the remaining eight variables. The score chi-square for a given variable is the value of the likelihood score test for testing the significance of the variable in the presence of LogBUN. The variable HGB is selected because it has the highest chi-square value (4.3468), and it is significant ( ) at the SLENTRY=0.25 level.
) at the SLENTRY=0.25 level.
Output 64.1.4 displays the fitted model containing both LogBUN and HGB. Based on the Wald statistics, neither LogBUN nor HGB is removed from the model.
| Convergence Status |
|---|
| Convergence criterion (GCONV=1E-8) satisfied. |
| Model Fit Statistics | ||
|---|---|---|
| Criterion | Without Covariates |
With Covariates |
| -2 LOG L | 309.716 | 297.767 |
| AIC | 309.716 | 301.767 |
| SBC | 309.716 | 305.509 |
Output 64.1.5 shows Step 3 of the selection process, in which the variable SCalc is added, resulting in the model with LogBUN, HGB, and SCalc as the explanatory variables. Note that SCalc has the smallest Wald chi-square statistic, and it is not significant (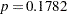 ) at the SLSTAY=0.15 level.
) at the SLSTAY=0.15 level.
| Convergence Status |
|---|
| Convergence criterion (GCONV=1E-8) satisfied. |
| Model Fit Statistics | ||
|---|---|---|
| Criterion | Without Covariates |
With Covariates |
| -2 LOG L | 309.716 | 296.078 |
| AIC | 309.716 | 302.078 |
| SBC | 309.716 | 307.692 |
The variable SCalc is then removed from the model in a step-down phase in Step 4 (Output 64.1.6). The removal of SCalc brings the stepwise selection process to a stop in order to avoid repeatedly entering and removing the same variable.
| Convergence Status |
|---|
| Convergence criterion (GCONV=1E-8) satisfied. |
| Model Fit Statistics | ||
|---|---|---|
| Criterion | Without Covariates |
With Covariates |
| -2 LOG L | 309.716 | 297.767 |
| AIC | 309.716 | 301.767 |
| SBC | 309.716 | 305.509 |
| Testing Global Null Hypothesis: BETA=0 | |||
|---|---|---|---|
| Test | Chi-Square | DF | Pr > ChiSq |
| Likelihood Ratio | 11.9493 | 2 | 0.0025 |
| Score | 12.7252 | 2 | 0.0017 |
| Wald | 12.1900 | 2 | 0.0023 |
The procedure also displays a summary table of the steps in the stepwise selection process, as shown in Output 64.1.7.
The stepwise selection process results in a model with two explanatory variables, LogBUN and HGB.
Copyright © SAS Institute, Inc. All Rights Reserved.