| The MULTTEST Procedure |
Example 58.3 Peto Mortality-Prevalence Test
This example illustrates the use of the Peto mortality-prevalence test. The test is a combination of analyses about the prevalence of incidental tumors in the population and mortality due to fatal tumors.
In the following data set, each observation represents an animal. The variables S1 S3 are three tumor types, with a value of 0 indicating no tumor, 1 indicating an incidental (nonlethal) tumor, and 2 indicating a lethal tumor. The time variable T indicates the time of death of the animal, a strata variable B is constructed from T, and the grouping variable Dose is drug dosage.
S3 are three tumor types, with a value of 0 indicating no tumor, 1 indicating an incidental (nonlethal) tumor, and 2 indicating a lethal tumor. The time variable T indicates the time of death of the animal, a strata variable B is constructed from T, and the grouping variable Dose is drug dosage.
data a; input S1-S3 T Dose @@; if T<=90 then B=1; else B=2; datalines; 0 0 0 104 0 2 0 1 80 0 0 0 1 104 0 0 0 0 104 0 0 2 0 100 0 1 0 0 104 0 2 0 0 85 1 2 1 0 60 1 0 1 0 89 1 2 0 1 96 1 0 0 0 96 1 2 0 1 99 1 2 1 1 60 2 2 0 0 50 2 2 0 1 80 2 0 0 2 98 2 0 0 1 99 2 2 1 1 50 2 ;
proc multtest data=a notables out=p stepsid; test peto(S1-S3 / permutation=20 time=T uppertailed); class Dose; strata B; contrast 'mort-prev' 0 1 2; run; proc print data=p; run;
The NOTABLES option in the PROC MULTTEST statement suppresses the display of the summary statistics for each variable. The OUT= option creates an output SAS data set p containing all p-values and intermediate statistics. The STEPSID option is used to adjust the p-values.
The TEST statement specifies an upper-tailed Peto test for S1 S3. The mortality strata are defined by TIME=T, the death times. The CLASS statement contains the grouping variable Dose. The prevalence strata are defined by the STRATA statement as the blocking variable B. The CONTRAST statement lists the default linear trend coefficients. The PROC PRINT statement displays the requested p-value data set.
S3. The mortality strata are defined by TIME=T, the death times. The CLASS statement contains the grouping variable Dose. The prevalence strata are defined by the STRATA statement as the blocking variable B. The CONTRAST statement lists the default linear trend coefficients. The PROC PRINT statement displays the requested p-value data set.
The results from this analysis are listed in Output 58.3.1 through Output 58.3.4.
The "Model Information" table in Output 58.3.1 displays information corresponding to the PROC MULTTEST invocation. In this case the totals for all prevalence and fatality strata are less than 20, so exact permutation tests are used everywhere, and the STEPSID adjustments are computed from these permutation distributions.
The contrast trend coefficients are listed in Output 58.3.2. They happen to be the same as the levels of the Dose variable.
In the "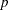 -Values" table in Output 58.3.3, the p-values for the Peto tests are listed in the Raw column, and the step-down Šidák adjusted p-values are in the Stepdown Šidák column.
-Values" table in Output 58.3.3, the p-values for the Peto tests are listed in the Raw column, and the step-down Šidák adjusted p-values are in the Stepdown Šidák column.
Significant p-values in the preceding table support the claim that higher dosage levels lead to higher mortality and prevalence. The raw Peto test is significant at the 5% level for S3, but the adjusted S3 test is no longer significant at 5%. The raw and adjusted p-values for S2 are the same because of the step-down technique.
The OUT= data set is displayed in Output 58.3.4.
| Obs | _test_ | _var_ | _contrast_ | _strat_ | _tstrat_ | _value_ | _exp_ | _se_ | raw_p | stpsid_p |
|---|---|---|---|---|---|---|---|---|---|---|
| 1 | PETO | S1 | mort-prev | 1 | 0 | 0 | 0.00000 | 0.00000 | . | . |
| 2 | PETO | S1 | mort-prev | 2 | 0 | 0 | 0.62500 | 0.85696 | . | . |
| 3 | PETO | S1 | mort-prev | 50 | 1 | 4 | 2.00000 | 1.12022 | . | . |
| 4 | PETO | S1 | mort-prev | 60 | 1 | 3 | 1.75000 | 1.06654 | . | . |
| 5 | PETO | S1 | mort-prev | 80 | 1 | 2 | 1.57143 | 1.04978 | . | . |
| 6 | PETO | S1 | mort-prev | 85 | 1 | 1 | 0.75000 | 0.72169 | . | . |
| 7 | PETO | S1 | mort-prev | 96 | 1 | 1 | 0.70000 | 0.78102 | . | . |
| 8 | PETO | S1 | mort-prev | 98 | 1 | 0 | 0.00000 | 0.00000 | . | . |
| 9 | PETO | S1 | mort-prev | 99 | 1 | 1 | 0.42857 | 0.72843 | . | . |
| 10 | PETO | S1 | mort-prev | 100 | 1 | 0 | 0.00000 | 0.00000 | . | . |
| 11 | PETO | S2 | mort-prev | 1 | 0 | 6 | 5.50000 | 1.05221 | . | . |
| 12 | PETO | S2 | mort-prev | 2 | 0 | 0 | 0.00000 | 0.00000 | . | . |
| 13 | PETO | S2 | mort-prev | 50 | 1 | 0 | 0.00000 | 0.00000 | . | . |
| 14 | PETO | S2 | mort-prev | 60 | 1 | 0 | 0.00000 | 0.00000 | . | . |
| 15 | PETO | S2 | mort-prev | 80 | 1 | 0 | 0.00000 | 0.00000 | . | . |
| 16 | PETO | S2 | mort-prev | 85 | 1 | 0 | 0.00000 | 0.00000 | . | . |
| 17 | PETO | S2 | mort-prev | 96 | 1 | 0 | 0.00000 | 0.00000 | . | . |
| 18 | PETO | S2 | mort-prev | 98 | 1 | 0 | 0.00000 | 0.00000 | . | . |
| 19 | PETO | S2 | mort-prev | 99 | 1 | 0 | 0.00000 | 0.00000 | . | . |
| 20 | PETO | S2 | mort-prev | 100 | 1 | 0 | 0.00000 | 0.00000 | . | . |
| 21 | PETO | S3 | mort-prev | 1 | 0 | 6 | 5.50000 | 1.05221 | . | . |
| 22 | PETO | S3 | mort-prev | 2 | 0 | 4 | 2.22222 | 1.08298 | . | . |
| 23 | PETO | S3 | mort-prev | 50 | 1 | 0 | 0.00000 | 0.00000 | . | . |
| 24 | PETO | S3 | mort-prev | 60 | 1 | 0 | 0.00000 | 0.00000 | . | . |
| 25 | PETO | S3 | mort-prev | 80 | 1 | 0 | 0.00000 | 0.00000 | . | . |
| 26 | PETO | S3 | mort-prev | 85 | 1 | 0 | 0.00000 | 0.00000 | . | . |
| 27 | PETO | S3 | mort-prev | 96 | 1 | 0 | 0.00000 | 0.00000 | . | . |
| 28 | PETO | S3 | mort-prev | 98 | 1 | 2 | 0.62500 | 0.85696 | . | . |
| 29 | PETO | S3 | mort-prev | 99 | 1 | 0 | 0.00000 | 0.00000 | . | . |
| 30 | PETO | S3 | mort-prev | 100 | 1 | 0 | 0.00000 | 0.00000 | . | . |
| 31 | PETO | S1 | mort-prev | . | . | 12 | 7.82500 | 2.42699 | 0.06808 | 0.08140 |
| 32 | PETO | S2 | mort-prev | . | . | 6 | 5.50000 | 1.05221 | 0.50000 | 0.50000 |
| 33 | PETO | S3 | mort-prev | . | . | 12 | 8.34722 | 1.73619 | 0.03627 | 0.07811 |
The first 30 observations correspond to intermediate statistics used to compute the Peto p-values. The _test_ variable lists the name of the test, the _var_ variable lists the name of the TEST variables, and the _contrast_ variable lists the CONTRAST label. The _strat_ variable lists the level of the STRATA variable, and the _tstrat_ variable indicates whether or not the stratum corresponds to values of the TIME= variable. The _value_ variable is the observed contrast for a stratum, and the _exp_ variable is its expected value. The variable _se_ contains the square root of the variance terms summed to form the denominator of the Peto statistics.
The final three observations correspond to the three Peto tests, with their p-values listed under the raw_p variable. The stpsid_p variable contains the step-down Šidák-adjusted p-values.
Copyright © SAS Institute, Inc. All Rights Reserved.