| The MIANALYZE Procedure |
| TEST Statement |
The TEST statement tests linear hypotheses about the parameters 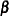 . An
. An 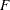 test is used to jointly test the null hypotheses (
test is used to jointly test the null hypotheses ( ) specified in a single TEST statement in which the MULT option is specified.
) specified in a single TEST statement in which the MULT option is specified.
Each equation specifies a linear hypothesis (a row of the  matrix and the corresponding element of the
matrix and the corresponding element of the  vector); multiple equations are separated by commas. The label, which must be a valid SAS name, is used to identify the resulting output. You can submit multiple TEST statements. When a label is not included in a TEST statement, a label of "Test
vector); multiple equations are separated by commas. The label, which must be a valid SAS name, is used to identify the resulting output. You can submit multiple TEST statements. When a label is not included in a TEST statement, a label of "Test  " is used for the
" is used for the  th TEST statement.
th TEST statement.
The form of an equation is as follows:
term < term
term  > < =
> < =  term <
term <  term
term  > >
> >
where term is a parameter of the model, or a constant, or a constant times a parameter. When no equal sign appears, the expression is set to 0. Only parameters for regressor effects (continuous variables by themselves) are allowed.
For each TEST statement, PROC MIANALYZE displays a "Test Specification" table of the  matrix and the
matrix and the  vector. The procedure also displays a "Variance Information" table of the between-imputation, within-imputation, and total variances for combining complete-data inferences, and a "Parameter Estimates" table of a combined estimate and standard error for each linear component. The linear components are labeled TestPrm1, TestPrm2, ... in the tables.
vector. The procedure also displays a "Variance Information" table of the between-imputation, within-imputation, and total variances for combining complete-data inferences, and a "Parameter Estimates" table of a combined estimate and standard error for each linear component. The linear components are labeled TestPrm1, TestPrm2, ... in the tables.
The following statements illustrate possible uses of the TEST statement:
proc mianalyze; modeleffects intercept a1 a2 a3; test1: test intercept + a2 = 0; test2: test intercept + a2; test3: test a1=a2=a3; test4: test a1=a2, a2=a3; run;
The first and second TEST statements are equivalent and correspond to the specification in Figure 55.5.
The third and fourth TEST statements are also equivalent and correspond to the specification in Figure 55.6.
The ALPHA= and EDF options specified in the PROC MIANALYZE statement are also applied to the TEST statement. You can specify the following options in the TEST statement after a slash(/):
For more information, see the section Testing Linear Hypotheses about the Parameters.
Copyright © SAS Institute, Inc. All Rights Reserved.
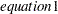 <, ..., <
<, ..., <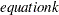 > > </
> > </  >
>