| The GLM Procedure |
Example 39.8 Mixed Model Analysis of Variance with the RANDOM Statement
Milliken and Johnson (1984) present an example of an unbalanced mixed model. Three machines, which are considered as a fixed effect, and six employees, which are considered a random effect, are studied. Each employee operates each machine for either one, two, or three different times. The dependent variable is an overall rating, which takes into account the number and quality of components produced.
The following statements form the data set and perform a mixed model analysis of variance by requesting the TEST option in the RANDOM statement. Note that the machine*person interaction is declared as a random effect; in general, when an interaction involves a random effect, it too should be declared as random. The results of the analysis are shown in Output 39.8.1 through Output 39.8.4.
data machine; input machine person rating @@; datalines; 1 1 52.0 1 2 51.8 1 2 52.8 1 3 60.0 1 4 51.1 1 4 52.3 1 5 50.9 1 5 51.8 1 5 51.4 1 6 46.4 1 6 44.8 1 6 49.2 2 1 64.0 2 2 59.7 2 2 60.0 2 2 59.0 2 3 68.6 2 3 65.8 2 4 63.2 2 4 62.8 2 4 62.2 2 5 64.8 2 5 65.0 2 6 43.7 2 6 44.2 2 6 43.0 3 1 67.5 3 1 67.2 3 1 66.9 3 2 61.5 3 2 61.7 3 2 62.3 3 3 70.8 3 3 70.6 3 3 71.0 3 4 64.1 3 4 66.2 3 4 64.0 3 5 72.1 3 5 72.0 3 5 71.1 3 6 62.0 3 6 61.4 3 6 60.5 ;
proc glm data=machine; class machine person; model rating=machine person machine*person; random person machine*person / test; run;
The TEST option in the RANDOM statement requests that PROC GLM determine the appropriate 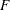 tests based on person and machine*person being treated as random effects. As you can see in Output 39.8.4, this requires that a linear combination of mean squares be constructed to test both the machine and person hypotheses; thus,
tests based on person and machine*person being treated as random effects. As you can see in Output 39.8.4, this requires that a linear combination of mean squares be constructed to test both the machine and person hypotheses; thus, 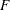 tests that use Satterthwaite approximations are needed.
tests that use Satterthwaite approximations are needed.
| Source | DF | Sum of Squares | Mean Square | F Value | Pr > F |
|---|---|---|---|---|---|
| Model | 17 | 3061.743333 | 180.102549 | 206.41 | <.0001 |
| Error | 26 | 22.686667 | 0.872564 | ||
| Corrected Total | 43 | 3084.430000 |
| Source | DF | Type III SS | Mean Square | F Value | Pr > F |
|---|---|---|---|---|---|
| machine | 2 | 1238.197626 | 619.098813 | 16.57 | 0.0007 |
| Error | 10.036 | 375.057436 | 37.370384 | ||
| Error: 0.9226*MS(machine*person) + 0.0774*MS(Error) | |||||
Note that you can also use the MIXED procedure to analyze mixed models. The following statements use PROC MIXED to reproduce the mixed model analysis of variance; the relevant part of the PROC MIXED results is shown in Output 39.8.5.
proc mixed data=machine method=type3; class machine person; model rating = machine; random person machine*person; run;
| Type 3 Analysis of Variance | ||||||||
|---|---|---|---|---|---|---|---|---|
| Source | DF | Sum of Squares | Mean Square | Expected Mean Square | Error Term | Error DF | F Value | Pr > F |
| machine | 2 | 1238.197626 | 619.098813 | Var(Residual) + 2.137 Var(machine*person) + Q(machine) | 0.9226 MS(machine*person) + 0.0774 MS(Residual) | 10.036 | 16.57 | 0.0007 |
| person | 5 | 1011.053834 | 202.210767 | Var(Residual) + 2.2408 Var(machine*person) + 6.7224 Var(person) | 0.9674 MS(machine*person) + 0.0326 MS(Residual) | 10.015 | 5.17 | 0.0133 |
| machine*person | 10 | 404.315028 | 40.431503 | Var(Residual) + 2.3162 Var(machine*person) | MS(Residual) | 26 | 46.34 | <.0001 |
| Residual | 26 | 22.686667 | 0.872564 | Var(Residual) | . | . | . | . |
The advantage of PROC MIXED is that it offers more versatility for mixed models; the disadvantage is that it can be less computationally efficient for large data sets. See Chapter 56, The MIXED Procedure, for more details.
Copyright © SAS Institute, Inc. All Rights Reserved.