| The GENMOD Procedure |
Example 37.4 Ordinal Model for Multinomial Data
This example illustrates how you can use the GENMOD procedure to fit a model to data measured on an ordinal scale. The following statements create a SAS data set called Icecream. The data set contains the results of a hypothetical taste test of three brands of ice cream. The three brands are rated for taste on a five-point scale from very good (vg) to very bad (vb). An analysis is performed to assess the differences in the ratings of the three brands. The variable taste contains the ratings, and the variable brand contains the brands tested. The variable count contains the number of testers rating each brand in each category.
The following statements create the Icecream data set:
data Icecream; input count brand$ taste$; datalines; 70 ice1 vg 71 ice1 g 151 ice1 m 30 ice1 b 46 ice1 vb 20 ice2 vg 36 ice2 g 130 ice2 m 74 ice2 b 70 ice2 vb 50 ice3 vg 55 ice3 g 140 ice3 m 52 ice3 b 50 ice3 vb ; run;
The following statements fit a cumulative logit model to the ordinal data with the variable taste as the response and the variable brand as a covariate. The variable count is used as a FREQ variable.
proc genmod data=Icecream rorder=data;
freq count;
class brand;
model taste = brand / dist=multinomial
link=cumlogit
aggregate=brand
type1;
estimate 'LogOR12' brand 1 -1 / exp;
estimate 'LogOR13' brand 1 0 -1 / exp;
estimate 'LogOR23' brand 0 1 -1 / exp;
run;
The AGGREGATE=BRAND option in the MODEL statement specifies the variable brand as defining multinomial populations for computing deviances and Pearson chi-squares. The RORDER=DATA option specifies that the taste variable levels be ordered by their order of appearance in the input data set—that is, from very good (vg) to very bad (vb). By default, the response is sorted in increasing ASCII order. Always check the "Response Profiles" table to verify that response levels are appropriately ordered. The TYPE1 option requests a Type 1 test for the significance of the covariate brand.
If 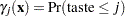 is the cumulative probability of the
is the cumulative probability of the 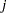 th or lower taste category, then the odds ratio comparing
th or lower taste category, then the odds ratio comparing 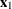 to
to 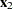 is as follows:
is as follows:
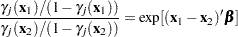 |
See McCullagh and Nelder (1989, Chapter 5) for details on the cumulative logit model. The ESTIMATE statements compute log odds ratios comparing each of brands. The EXP option in the ESTIMATE statements exponentiates the log odds ratios to form odds ratio estimates. Standard errors and confidence intervals are also computed.
Output 37.4.1 displays general information about the model and data, the levels of the CLASS variable brand, and the total number of occurrences of the ordered levels of the response variable taste.
Output 37.4.2 displays estimates of the intercept terms and covariates and associated statistics. The intercept terms correspond to the four cumulative logits defined on the taste categories in the order shown in Output 37.4.1. That is, Intercept1 is the intercept for the first cumulative logit, 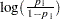 , Intercept2 is the intercept for the second cumulative logit,
, Intercept2 is the intercept for the second cumulative logit,  , and so forth.
, and so forth.
| Analysis Of Maximum Likelihood Parameter Estimates | ||||||||
|---|---|---|---|---|---|---|---|---|
| Parameter | DF | Estimate | Standard Error | Wald 95% Confidence Limits | Wald Chi-Square | Pr > ChiSq | ||
| Intercept1 | 1 | -1.8578 | 0.1219 | -2.0967 | -1.6189 | 232.35 | <.0001 | |
| Intercept2 | 1 | -0.8646 | 0.1056 | -1.0716 | -0.6576 | 67.02 | <.0001 | |
| Intercept3 | 1 | 0.9231 | 0.1060 | 0.7154 | 1.1308 | 75.87 | <.0001 | |
| Intercept4 | 1 | 1.8078 | 0.1191 | 1.5743 | 2.0413 | 230.32 | <.0001 | |
| brand | ice1 | 1 | 0.3847 | 0.1370 | 0.1162 | 0.6532 | 7.89 | 0.0050 |
| brand | ice2 | 1 | -0.6457 | 0.1397 | -0.9196 | -0.3719 | 21.36 | <.0001 |
| brand | ice3 | 0 | 0.0000 | 0.0000 | 0.0000 | 0.0000 | . | . |
| Scale | 0 | 1.0000 | 0.0000 | 1.0000 | 1.0000 | |||
| Note: | The scale parameter was held fixed. |
The Type 1 test displayed in Output 37.4.3 indicates that Brand is highly significant; that is, there are significant differences among the brands. The log odds ratios and odds ratios in the "ESTIMATE Statement Results" table indicate the relative differences among the brands. For example, the odds ratio of 2.8 in the "Exp(LogOR12)" row indicates that the odds of brand 1 being in lower taste categories is 2.8 times the odds of brand 2 being in lower taste categories. Since, in this ordering, the lower categories represent the more favorable taste results, this indicates that brand 1 scored significantly better than brand 2. This is also apparent from the data in this example.
| LR Statistics For Type 1 Analysis | ||||
|---|---|---|---|---|
| Source | Deviance | DF | Chi-Square | Pr > ChiSq |
| Intercepts | 65.9576 | |||
| brand | 9.8654 | 2 | 56.09 | <.0001 |
| Contrast Estimate Results | ||||||||||
|---|---|---|---|---|---|---|---|---|---|---|
| Label | Mean Estimate | Mean | L'Beta Estimate | Standard Error | Alpha | L'Beta | Chi-Square | Pr > ChiSq | ||
| Confidence Limits | Confidence Limits | |||||||||
| LogOR12 | 0.7370 | 0.6805 | 0.7867 | 1.0305 | 0.1401 | 0.05 | 0.7559 | 1.3050 | 54.11 | <.0001 |
| Exp(LogOR12) | 2.8024 | 0.3926 | 0.05 | 2.1295 | 3.6878 | |||||
| LogOR13 | 0.5950 | 0.5290 | 0.6577 | 0.3847 | 0.1370 | 0.05 | 0.1162 | 0.6532 | 7.89 | 0.0050 |
| Exp(LogOR13) | 1.4692 | 0.2013 | 0.05 | 1.1233 | 1.9217 | |||||
| LogOR23 | 0.3439 | 0.2850 | 0.4081 | -0.6457 | 0.1397 | 0.05 | -0.9196 | -0.3719 | 21.36 | <.0001 |
| Exp(LogOR23) | 0.5243 | 0.0733 | 0.05 | 0.3987 | 0.6894 | |||||
Copyright © SAS Institute, Inc. All Rights Reserved.